ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ. 1. Включить измерительный прибор

1. Включить измерительный прибор. При работе на установке С3-2 выбрать номинал сопротивлений (500 или 1000 Ом).

2. Провести измерение сопротивлений резисторов ( для установки С3-1 и для установки С3-2), и результаты измере-ний 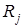занести в таблицу 1а (для установки С3-2) или 1б (для уста-новки С3-2).

Таблица 1а

Результаты измерений

№ переключателя	П о л о ж е н и е
					…

Таблица 1б

Результаты измерений

№ переключа-теля	П о л о ж е н и е
…

3. Составить статистический ряд по следующей схеме:

– определить максимальное и минимальное значения среди по-лученных результатов и разбить диапазон принимаемых значений на одинаковых интервалов с границами , ( ).

– подсчитать число 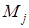значений сопротивлений, попавших в интервал.

– вычислить частоту попаданий результатов в интервал с номе-ром в общем числе измерений, используя формулу (3.1.2).

4. Рассчитать среднее значение для каждого интервала по формуле: .

5. Используя выражение (3.1.6) по полученным выше результа-там, вычислить среднее значение 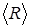(или математическое ожида-ние случайной величины).

6. По формулам (3.1.8) и (3.1.9) определить дисперсию 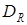, среднее квадратичное отклонение 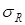и величину .

7. Результаты вычислений пп. 3–6 занести в таблицу 2.

8. Вычислить границы интервала . Определить значения сопротивлений, не попадающие в этот интервал.

9. Аккуратно зачеркнуть значения сопротивлений, выпадающих из интервала , в таблице 1.

10. Выполнить п.п.3-7 без учета вычеркнутых значений. Резуль-таты занести в таблицу 3, построенную аналогично таблице 2.

8. Используя вычисленные величины 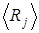и 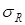, рассчитать зна-чения 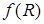для средних значений 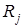малых интервалов 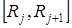. Результаты занести в таблицу 3.

9. По полученным расчетным данным построить гистограмму и график функции .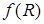

10. Сравнить форму огибающей гистограммы и графика . Объяснить качественные различия и сходство зтих двух кривых.

Таблица 2

Результаты вычислений

…
			=	=	=	=

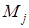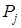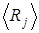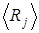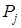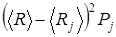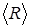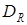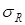КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какой процесс называется случайным?

2. Что такое случайная величина?

3. Какая величина называется частотой события?

4. Что называется законом распределения случайной величины?

5. Что такое функция распределения случайной величины?

6. Запишите основные свойства функции распределения случай-ной величины.

7. Укажите основные числовые параметры, характеризующие закон распределения случайной величины и объясните их смысл.

8. Что называется математическим ожиданием случайной вели-чины?

9. Дайте определение величины дисперсии.

10. Что называется средним квадратичным отклонением?

11. В чем удобство использования среднего квадратичного от-клонения по сравнению с использованием дисперсии?

12. Какова связь между функцией распределения и плотностью распределения?

13. Для каких случайных величин существует плотность распре-деления– дискретных или непрерывных?

14. Запишите основные свойства плотности распределения.

15. Что такое кривая распределения?

16. Запишите выражение для функции плотности распределения непрерывной случайной величины.

17. Какова вероятность принятия случайной величиной конкрет-ного значения при дискретном распределении? При непрерывном распределении?

18. Как влияет дисперсия случайной величины на форму кривой распределения?

19. Укажите аналог кривой распределения для дискретных слу-чайных величин.

20. Укажите оценку основных параметров распределения.

21. Какая оценка называется точечной?

22. Какая оценка называется несмещённой?

23. Что такое доверительная вероятность или надежность изме-рения?

24. Как измеряется доверительный интервал для среднего значе-ния измеряемой величины и что он обозначает?

25. В классической физике имеет место классическое распреде-ление Максвелла. Что это за распределение и чем оно отличается от нормального распределения?

26. В чем заключается «правило трех сигм»?

27. Как «правило трех сигм» позволяет отсеивать недостовер-ные результаты?

28. Как составляется статистический ряд?

29. Как производится построение гистограммы?

30 Как по гистограмме получить характеристики распределения случайной величины?