Алгоритм симплекс-метода
Пусть имеется ЗЛП (1.6). Из предыдущего параграфа вытекает, что для нахождения решения ЗЛП достаточно последовательно перебрать угловые точки (число которых конечное) области допустимых решений задачи и выбрать ту, в которой достигается экстремум целевой функции. На этом строится симплекс-метод решения ЗЛП, алгоритм которого - следующий:
1. Привести задачу к каноническому виду.
2. С помощью метода Жордана-Гаусса найти очередное опорное решение.
3. Проверить на оптимальность очередное опорное решение. Если оно оптимальное, то задача решена. В противном случае перейти к пункту 2.
Опорное решение, полученное на первом шаге, называется первоначальным опорным планом.
Для нахождения первоначального опорного плана (после приведения задачи к каноническому виду) поступаем следующим образом:
1. Из векторов условий A1, A2, …, An включаем в базис те, которые являются стандартными единичными (то есть те, у которых все координаты нулевые, кроме одной, которая равна 1; среди них обязательно окажутся те, которые соответствуют дополнительным переменным с положительным знаком). Соответствующие переменные будут включены в базис. Если число таких векторов условий равно m, то первоначальный опорный план построен: им является решение системы ограничений, полученное приравниванием свободных переменных к 0. В противном случае идём к пункту 2.
2. Допустим, переменная xk пока не вошла в базис. Тогда выбираем уравнение, в котором отношение  (где aik>0) будет минимальным. Это (i-е) уравнение будет ведущим: разделив его на коэффициент aik при xk, добиваемся, чтобы коэффициент при xk стал равным 1, а из остальных уравнений xk исключаем (применяем метод Жордана-Гаусса). Процесс продолжаем до тех пор, пока базис не будет содержать m переменных.
(где aik>0) будет минимальным. Это (i-е) уравнение будет ведущим: разделив его на коэффициент aik при xk, добиваемся, чтобы коэффициент при xk стал равным 1, а из остальных уравнений xk исключаем (применяем метод Жордана-Гаусса). Процесс продолжаем до тех пор, пока базис не будет содержать m переменных.
Если во всех уравнениях коэффициент при xk будет неположительным (то есть aik£0), то xk нельзя включать в базис. Кроме того, если минимум чисел  достигается в уравнении, в котором имеется базисная переменная xl, то при включении xk в базис переменная xl из базиса исключится. Поэтому для включения в базис очередной переменной xk (без исключения из базиса другой) необходимо в качестве базисной выбрать такую переменную, чтобы минимум чисел
достигается в уравнении, в котором имеется базисная переменная xl, то при включении xk в базис переменная xl из базиса исключится. Поэтому для включения в базис очередной переменной xk (без исключения из базиса другой) необходимо в качестве базисной выбрать такую переменную, чтобы минимум чисел  достигался в уравнении, не содержащем базисных переменных.
достигался в уравнении, не содержащем базисных переменных.
Пример 1. Найти первоначальный опорный план задачи:
-3x1+x2+2x3®max(min)
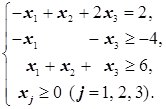
Решение. Решим задачу вначале «вручную».
1. Приведём задачу к каноническому виду. Для этого сначала умножим второе неравенство системы ограничений на (-1) (добиваемся, чтобы правые части всех нетривиальных ограничений имели знак «+»). Получаем систему ограничений
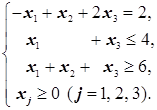
Теперь добавляем во второе и третье неравенства системы дополнительные переменные x4 и x5:
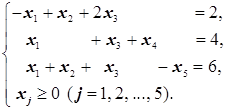
Таким образом, получаем канонический вид исходной задачи:
-3x1+x2+2x3®max(min)
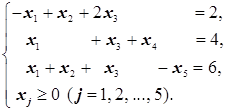
2. С помощью метода Жордана-Гаусса найдём первоначальный опорный план. Прежде всего замечаем, что дополнительная переменная x4 входит только во второе уравнение. И она уже в базисе. Так как для x2 min 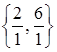 =2 достигается в первом уравнении (при определении этого min второе уравнение не участвует, так как коэффициент при x2 в нём равен 0), то x2 включаем в базис, исключив его из третьего уравнения (для этого первое уравнение вычитаем из третьего):
=2 достигается в первом уравнении (при определении этого min второе уравнение не участвует, так как коэффициент при x2 в нём равен 0), то x2 включаем в базис, исключив его из третьего уравнения (для этого первое уравнение вычитаем из третьего):

Две базисные переменные из первого и второго уравнений выбраны. Осталось выбрать третью базисную переменную из третьего уравнения. Переменные x3 и x5 для этого не годятся, так как коэффициенты при них отрицательны. Остаётся только x1. Для того, чтобы её ввести в базис необходимо, чтобы минимум отношений свободных членов к положительным коэффициентам достигался в третьем уравнении. Так оно и есть: min  =2 достигается в третьем уравнении. Поэтому третье уравнение делим на 2, затем прибавляем его к первому и вычитаем из второго:
=2 достигается в третьем уравнении. Поэтому третье уравнение делим на 2, затем прибавляем его к первому и вычитаем из второго:
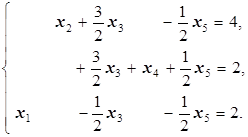
Таким образом, при x3=0, x5=0 имеем x1=2, x2=4, x4=2 и X1=(2; 4; 0; 2; 0) - первоначальный опорный план.
Ответ: X1=(2; 4; 0; 2; 0) - первоначальный опорный план.
Проверка опорного плана на оптимальность проводится по следующей схеме:
1. Находятся оценки Dk=CбAk-ck= 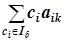 -ck для всех k=0, 1, …, n. При этом D0 - это значение целевой функции при данном опорном плане, и Dk=0 для всех базисных переменных xk (то есть последние вычислять необязательно, а достаточно сразу положить Dk=0).
-ck для всех k=0, 1, …, n. При этом D0 - это значение целевой функции при данном опорном плане, и Dk=0 для всех базисных переменных xk (то есть последние вычислять необязательно, а достаточно сразу положить Dk=0).
2. Если условие оптимальности опорного плана выполнено (Dk³0 для всех k=1, …, n при поиске максимума, Dk£0 для всех k=1, …, n при поиске минимума), то задача решена. В противном случае переходят к другому опорному плану.
Переход к другому опорному плану проводится по следующей схеме:
1. Для всех Dk, для которых нарушается условие оптимальности задачи, вычисляются qk=  , а по ним - величины -qkDk.
, а по ним - величины -qkDk.
2. Выбирается xk такой, что |-qkDk| является максимальным. Эту xk и вводим в базис, выводя из него xi, в которой достигается минимальное qk, по методу Жордана-Гаусса.
Пример 2. Решить задачу предыдущего примера (найти экстремумы).
Решение. При решении предыдущего примера канонический вид задачи и её первоначальный опорный план найдены.
Проверим на оптимальность решение X1. Для этого необходимо вычислить Dk=CбAk-ck для k - индексов свободных переменных. При k=3 имеем
D3=CбA3-c3=(1, 0, -3)× 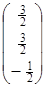 -2=1×
-2=1× 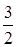 +0×
+0× 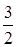 +(-3)×
+(-3)× 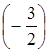 -2=1,
-2=1,
то есть D3=1≥0. В частности, в X1 минимум не достигается.
D5=CбA5-c5=(1, 0, -3)× 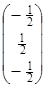 -0=1×
-0=1×  +0×
+0×  +(-3)×
+(-3)×  =1,
=1,
то есть D5=1≥0. Так как Dk≥0 для всех k=1, 2, 3, 4, 5, то в X1 достигается максимум целевой функции, который равен D0=CX=-3×2+4+2×0=-2. Минимум в этой точке не достигается.
Перейдём к другому опорному плану. Для D3 и D5, для которых нарушается условие оптимальности, вычислим q3 и q5, а по ним - величины -q3D3 и -q5D5:
q3=  =
= 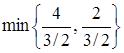 =
= 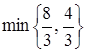 =
= 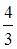 (достигается при x4),
(достигается при x4),
-q3D3=- 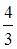 ×1=-
×1=- 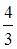 ,
,
q5=  =
= 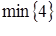 =4, (достигается снова при x4, то есть в любом случае x4 будем выводить из базиса),
=4, (достигается снова при x4, то есть в любом случае x4 будем выводить из базиса),
-q5D5=-4×1=-4.
Так как |-q5D5|=|-4|>|- 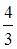 |=|-q3D3|, то в базис будем вводить x5 вместо x4. Для этого второе уравнение прибавляем к первому и третьему, и умножаем его на 2:
|=|-q3D3|, то в базис будем вводить x5 вместо x4. Для этого второе уравнение прибавляем к первому и третьему, и умножаем его на 2:
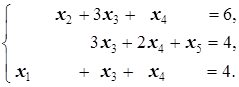
Получили новый опорный план X2=(4; 6; 0; 0; 4), который проверяем на оптимальность:
D3=CбA3-c3=(1, 0, -3)×  -2=1×3+0×3+(-3)×1-2=-2,
-2=1×3+0×3+(-3)×1-2=-2,
D4=CбA4-c4=(1, 0, -3)×  -0=1×1+0×2+(-3)×1-0=-2.
-0=1×1+0×2+(-3)×1-0=-2.
Таким образом, D3=-2<0, D4=-2<0, то есть Dk≤0 для всех k=1, 2, 3, 4, 5. Значит, X2 - оптимальное решение задачи с точки зрения минимизации. В нём CX=-3×4+6+2×0=-6.
Ответ: Fmin=-6, минимум достигается в точке X2=(4; 6; 0);
Fmax=-2, максимум достигается в точке X1=(2; 4; 0).
Симплекс-таблицы.
Все вычисления в симплекс-методе принято производить в таблицах. Прежде всего, в отдельных таблицах вида
| №№ ур-й | Своб. члены | A1 | A2 | … | An | qk |
| b1 | a11 | a12 | … | a1n | b1/a1k (a1k>0) | |
| b2 | a21 | a22 | … | a2n | b2/a2k (a2k>0) | |
| … | … | … | … | … | … | … |
| m | bm | am1 | am2 | … | amn | bm/amk (amk>0) |
производятся преобразования Жордана-Гаусса. Затем составляется симплекс-таблица вида
| Базис | Сб | Своб. члены | c1 | c2 | … | cn | q1 | q2 | … | qn |
| A1 | A2 | … | An | |||||||
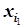 | 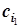 | b1 | a11 | a12 | … | a1n | … | |||
 |  | b2 | a21 | a22 | … | a2n | … | |||
| … | … | … | … | … | … | … | … | … | … | … |
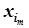 | 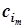 | bm | am1 | am2 | … | amn | … | |||
| Dk | D1 | D1 | D2 | … | Dn | -q1D1 | -q2D2 | … | -qnDn |
в которой Dk=0 сразу проставляются для всех базисных векторов условий и Dk=CбAk-ck для небазисных, столбцы qk вычисляются только для свободных переменных xk, наконец, для тех из них, для которых не выполнено условие оптимальности, вычисляются -qkDk, и из них выбирается наибольший по абсолютной величине. Тот xk, для которого достигается этот максимум, вводится в базис.
Продемонстрируем применение таблиц при решении нашего предыдущего примера.
I этап. Нахождение первоначального опорного плана:
| Табл.1 | №№ ур-й | Своб. члены | x1 | x2 | x3 | x4 | x5 | qk | |
| -1 | 2/1 | min, k=2 | |||||||
| - | |||||||||
| -1 | 6/1 | ||||||||
| Табл.2 | -1 | - | |||||||
| 4/1 | |||||||||
| -1 | -1 | 4/2 | min, k=1 | ||||||
| Табл.3 | 3/2 | -1/2 | |||||||
| 3/2 | 1/2 | ||||||||
| -1/2 | -1/2 |
Напоминаем, что в базис включаем x2. Имеем, что минимум min 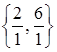 =2 отношений свободных членов системы к положительным коэффициентам достигается в первой строке. При переходе к Табл.2 первые две строки Табл.1 перенесли в Табл.2. Третью строку табл.2 получили, вычтя из третьей строки (Табл.1) первую строку.
=2 отношений свободных членов системы к положительным коэффициентам достигается в первой строке. При переходе к Табл.2 первые две строки Табл.1 перенесли в Табл.2. Третью строку табл.2 получили, вычтя из третьей строки (Табл.1) первую строку.
В Табл.3 в базис включаем x1. Имеем min 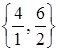 =2 в третьей строке. Третью строку Табл.2 делим на 2 - получаем третью строку Табл.3. Затем третью строку прибавляем к первой строке и вычитаем из второй строки Табл.2. Получаем первую и вторую строки Табл.3.
=2 в третьей строке. Третью строку Табл.2 делим на 2 - получаем третью строку Табл.3. Затем третью строку прибавляем к первой строке и вычитаем из второй строки Табл.2. Получаем первую и вторую строки Табл.3.
II этап. Применение симплекс-метода.
| Базис | Сб | Своб. члены | -3 | q1 | q2 | q3 | q4 | q5 | ||||||
| x1 | x2 | x3 | x4 | x5 | ||||||||||
| x2 | 3/2 | -1/2 | - | - | 8/3 | - | - | |||||||
| x4 | 3/2 |
| - | - | 4/3 | - | ||||||||
| x1 | -3 | -1/2 | -1/2 | - | - | - | - | - | ||||||
| Dk | -2 | - | - | -4/3 | - | -4 | ||||||||
| x2 | ||||||||||||||
| x5 | ||||||||||||||
| x1 | -3 | |||||||||||||
| Dk | -6 | -2 | -2 | |||||||||||
Комментарии опустим, предложив читателю восстановить применение метода к таблицам.
4.3. Упражнение. Решить задачи линейного программирования Упражнения 1.3 симплекс-методом.
