Постановка задачи синтеза робастного управления, обеспечивающего стабилизацию маятника при неопределенных возмущениях и параметрических изменениях (для примера 2-го порядка)
Регуляторы, синтезированные по линеаризованной модели, обеспечивают устойчивость и требуемое качество линейной системы при фиксированных значениях параметров. Такой регулятор способен стабилизировать нелинейную систему только вблизи состояния равновесия при заданных значениях параметров. Для того чтобы система стабилизировалась при других значениях параметров, несколько отличающихся от исходных, требуется синтезировать робастный (грубый – нечувствительный по отношению к изменению параметров и возможно нелинейностям) регулятор.
Рассмотрим снова пример системы из п.1.1:
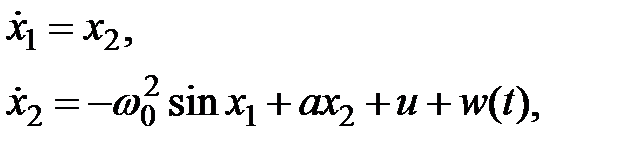 (5.1)
(5.1)
которую будем рассматривать как систему
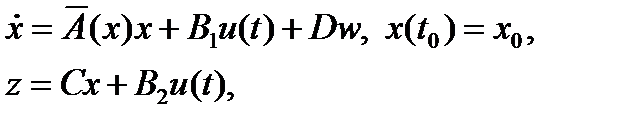 (5.2)
(5.2)
где  - вектор состояния,
- вектор состояния,  - входное возмущение,
- входное возмущение, 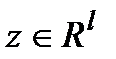 - вектор управляемого выхода,
- вектор управляемого выхода, 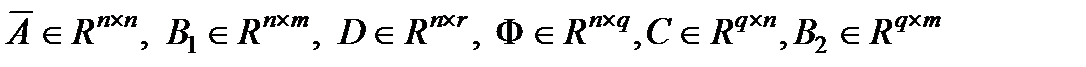 - известные постоянные матрицы,
- известные постоянные матрицы,  , T>t0 заданная константа (при рассмотрении на конечном интервале) или T=¥ (при рассмотрении на бесконечном интервале).
, T>t0 заданная константа (при рассмотрении на конечном интервале) или T=¥ (при рассмотрении на бесконечном интервале).
Предположим, что неопределенные возмущения являются непрерывными функциями, ограниченными в каждый момент времени:
 . (5.3)
. (5.3)
Множество таких функций обозначим как W=Ew(I).
В качестве выхода системы, чтобы избежать больших значений управления, выбран вектор  . Также будет учитываться неопределенность в начальном состоянии системы, задаваемая в виде эллипсоида с матрицей
. Также будет учитываться неопределенность в начальном состоянии системы, задаваемая в виде эллипсоида с матрицей  , т.е.
, т.е.
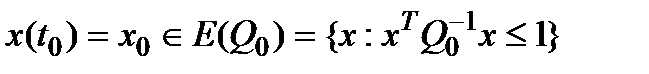 (5.4)
(5.4)
При этом для рассматриваемой системы (1.1) определим матрицы в (1.2)
 .
.
Предполагается, что значение параметр  в процессе может изменяться и отклоняться от своего номинального значения
в процессе может изменяться и отклоняться от своего номинального значения  на величину
на величину  , для которого имеет место ограничение
, для которого имеет место ограничение
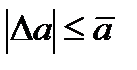 ,
,
где  - известная положительная константа.
- известная положительная константа.
Линеаризованная система относительно положения равновесия x=0 получается из исходной заменой нелинейной функции  ее средним значением, которое согласно графику, показанному на рисунке 5.1 составляет 0.392:
ее средним значением, которое согласно графику, показанному на рисунке 5.1 составляет 0.392:
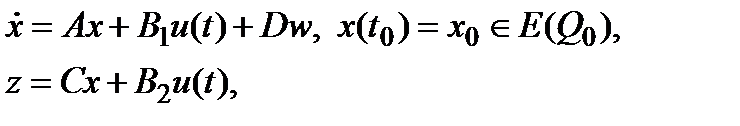 (5.5)
(5.5)
где матрица A определяется как 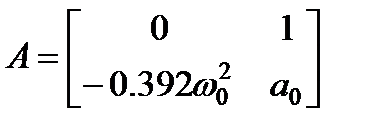 .
.

Рисунок 5.1. График функции 0.392–sin(x)/x
Обозначим  , где
, где 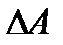 - матрица, характеризующая отклонения матрицы
- матрица, характеризующая отклонения матрицы 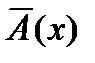 от матрицы A при изменении параметров
от матрицы A при изменении параметров 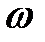 , a и координаты x1 вектора состояния. Представим матрицу
, a и координаты x1 вектора состояния. Представим матрицу 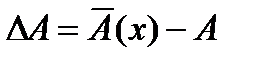 в виде
в виде
 (5.6)
(5.6)
(матрицы со структурированными неопределенностями), где матрица D содержит элементы, которые зависят от неопределенных параметров, а матрицы M, N – содержат элементы, не зависящие от неопределенных параметров. В рассматриваемом случае определим
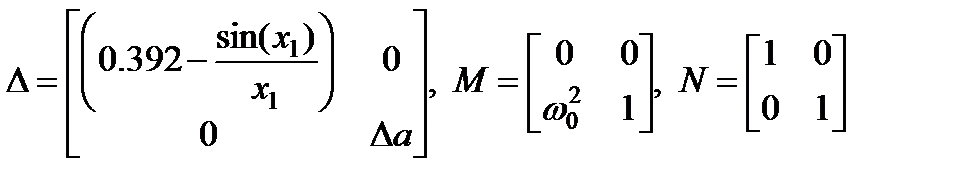 .
.
Прямой проверкой убеждаемся, что 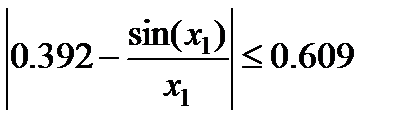 при всех x1. Поэтому при
при всех x1. Поэтому при  получаем, что ограничение
получаем, что ограничение
 (5.7)
(5.7)
выполняется при g=0.621.
Таким образом, требуется синтезировать робастный регулятор для системы (5.2) с неопределенными возмущениями из (5.3) и параметрическими изменениями, представленными в виде (5.6) с матрицей D, удовлетворяющей ограничению (5.7), обеспечивающий стабилизацию с максимальной точностью.
