Случайная величина и ее распределение

Случайная величина является одним из основных понятий теории вероятностей. Рассмотрим некоторые примеры, разъясняющие смысл случайной величины.

При последовательном бросании монеты несколько раз число появлений «орла» является переменной величиной, принимающей значения 0, 1, 2, ... в зависимости от случайных обстоятельств.

Интервал времени между двумя последовательными появлениями автобуса на данной остановке также является переменной величиной, подверженной различным колебаниям в зависимости от многих причин, учесть которые мы не в состоянии.

Рассматриваемая в этих примерах переменная величина обладает характерной особенностью. Хотя мы можем указать область ее возможных значений, однако мы не можем заранее знать, какое конкретное значение примет эта переменная величина, так как оно зависит от случая и меняется от испытания к испытанию.

Определение: Переменную величину, которая в результате испытания может принять лишь одно возможное значение, заранее не известное и зависящее от случайных причин, называют случайной величиной.

Для изучения случайной величины необходимо указать не только область ее возможных значений, но и то, как часто принимается этой величиной определенное значение, т. е. вероятность этих значений.

Определение: Соответствие между областью возможных значений случайной величины и множеством вероятностей этих значений носит название закона распределения случайной величины.

В зависимости от характера области возможных значений можно выделить два вида случайных величин: дискретные и непрерывные. Функцию, устанавливающую соответствие между областью возможных значений и множеством вероятностей для каждого вида случайных величин, можно задать разными способами.

Будем обозначать случайные величины большими латинскими буквами X, Y, T, ... , а соответствующие значения, которые они принимают, малыми буквами x, y, t, ... .

Определение: Случайная величина называется дискретной, если она принимает конечное или счетное число значений.

Дискретная случайная величина задается с помощью ряда распределения – функции, ставящей в соответствие каждому возможному значению случайной величины определенную вероятность. Таким образом, ряд распределения – это конечное или счетное множество пар элементов:

{x_i, p_i }, i = 1, 2, ... ; p_i = P(X = x_i).

Так как случайная величина X примет обязательно какое-нибудь из своих возможных значений x_i , сумма вероятностей p_i всех возможных значений равна единице.

Ряд распределения удобно изображать в виде таблицы:

X			…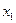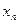
P			…

В первой строке указаны возможные значения x_i дискретной случайной величины X, а во второй – соответственно вероятности того, что X примет значение x_i.

Пусть дискретная случайная величина задана законом распределения в виде таблицы

X
P	0,2	0,4	0,3	0,1

Графическое изображение ряда распределения называется многоугольником распределения. Для его построения возможные значения x_i случайной величины откладываются по оси абсцисс, а вероятности – по оси ординат; точки с координатами (x_i, p_i) соединяются отрезками

Задача. Найти ряд распределения случайной величины, являющейся частотой выпадения «орла» при трех бросаниях монеты. Построить полигон распределения вероятностей.

Решение: Возможные значения частоты X выпадения «орла» следующие: 0, 1, 2, 3. Соответствующие вероятности нетрудно подсчитать путем учета благоприятствующих каждому значению частоты случаев при числе всех возможных случаев, равных 8:

P(X = 0) = 0,125,

P(X = 1) = 0,375,

Р(X = 2) = 0,375,

P(X = 3) = 0,125; контроль: 0,125 + 0,375 + 0,375 + 0,125 = 1.

Таким образом, получим закон распределения в виде:

X
P	0,125	0,375	0,375	0,125

Непрерывная случайная величина принимает возможные значения, заполняющие сплошь заданный интервал.

Определение: Плотностью вероятности j(х) непрерывной случайной величины Х называется производная ее функции распределения j(х) = F^/(x).

Задача.Функция распределения случайной величины Х имеет вид:

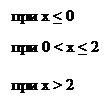
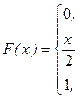
Найти плотность вероятности непрерывной случайной величины Х.

Заметим, что для удобства изучения непрерывных случайных величин плотность распределения определяют не на конечном интервале возможных значений случайной величины, а на всей действительной числовой прямой, полагая p(x) тождественно равной нулю для x, лежащих вне интервала возможных значений случайной величины.

Наиболее общим способом задания различных по своей природе случайных величин является функция распределения случайной величины (интегральный закон распределения).

Функция распределения

Функцией распределения F(x) случайной величины X, принимающей любое действительное значение x, называется вероятность того, что случайная величина X примет значение меньшее, чем x, т. е.

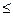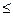F(x) = P(X < x) , причем 0 F(X) 1.

Теорема. Функция распределения обладает следующими свойствами:

1. , монотонное неубывание;

2. , непрерывность слева;

3. , .

Для дискретной случайной величины функция распределения F(x) может быть записана в виде:

.

Для непрерывной случайной величины интегральный закон выражается формулой:

,

где функция f(t) является плотностью распределения, удовлетворяющей двум условиям:

1) f(t) > 0;

2) . Неотрицательность и нормированность.

Вероятность .