Спектральный анализ одиночного радиоимпульса

Несущая частота радиоимпульса (частота заполнения):

, ,

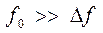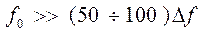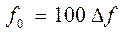
Определим ширину спектра Δf:

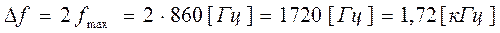
f_max– определена по графику амплитудного спектра одиночного прямоугольного видеоимпульса (рис.5), по 10% уровню от |S(f)| _max , т.е. по уровню 0.1|S(f)| _max .

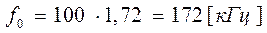
К узкополосным сигналам (радиосигналам) относятся сигналы, спектры которых сосредоточены в относительно узкой по сравнению со средней частотой полосе. Узкополосный сигнал описывается выражением:

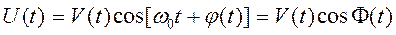, (5)

ω₀ – частота несущего колебания

V(t), Φ(t) – амплитуда и фаза сигнала

В частном случае, когда 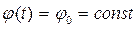, а V(t)=s(t) – непериодический видеосигнал, (5) описывает радиоимпульс:

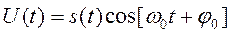, (6)

Таким образом, аналитическое выражение для полученного радиоимпульса:

,

где S(t) – заданный сигнал (см.. п.1)

Временная диаграмма одиночного радиоимпульса представлена на рис.8.

Спектральная плотность радиоимпульса определяется спектральной плотностью его огибающей:

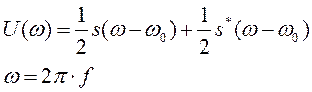
Спектр радиоимпульса U(ω) получается путём переноса спектра его огибающей S(ω) из окрестности нулевой частоты в окрестность несущей частоты ±ω₀ (с коэффициентом 1/2):

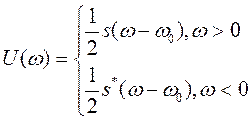
S(2π( f–f₀ )) и S(2π( f+f₀ )) – спектральные плотности видеоимпульса, составляющих заданный сигнал, определённые в п.1.

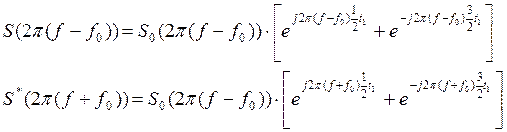
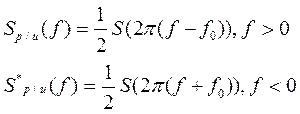
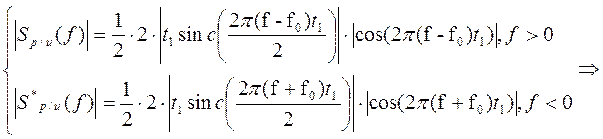
t₁=3мс

Амплитудный спектр радиоимпульса:

График при f<0 симметричен графику при в f>0 относительно оси ординат.

График амплитудного спектра одиночного радиоимпульса представлен на рис. 9.

4. Спектральный анализ периодической последовательности радиоимпульсов.

Спектральный анализ сигнала в виде периодической последовательности радиоимпульсов основан на его представлении в виде ряда Фурье:

,

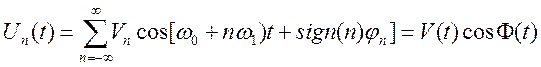коэффициенты которого связаны с коэффициентами ряда Фурье периодического видеосигнала (3) соотношением:

V_n – амплитудный спектр периодической последовательности радиоимпульсов.

Аналитическое выражение для последовательности радиоимпульсов:

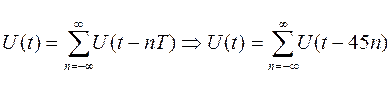
U(t) – одиночный радиоимпульс

или

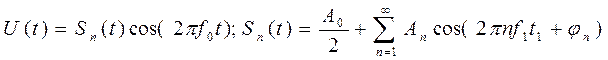
Временная диаграмма периодической последовательности радиоимпульсов представлена на рис.10.

,

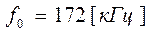
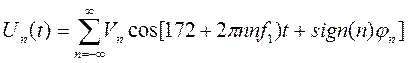
Определим амплитудный спектр периодической последовательности радиоимпульсов по:

График амплитудного спектра периодической последовательности радиоимпульсов V_n представлен на рис.11

5. Корреляционный анализ непериодического сигнала

Автокорреляционная функция определяется следующим интегралом:

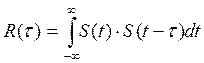, (7)

и характеризует взаимосвязь между значениями сигнала в различные моменты времени.

Для действительного сигнала корреляционная функция является действительной чётной функцией

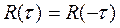
Максимального значения, равного энергии сигнала корреляционная функция достигает при τ=0:

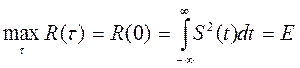
Непосредственное интегрирование в формуле (7) даёт выражение для правой ветви автокорреляционной функции (рис.)

Замена в полученном выражении τ =| τ | позволяет перейти к аналитическому описанию автокорреляционной функции, как для положительных значений τ>0, так и для отрицательных τ<0.

По свойствам автокорреляционной функции

S(t±t₀), t₀>0 => R(τ)=R(τ)

Корреляционная функция пачки импульсов

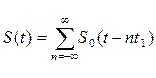, где S(t) – 1-й импульс в пачке,

при условии, что интервал следования в пачке t₁ больше или равен τ₀ – длительность 1-го импульса в пачке S₀(t), взаимосвязана с корреляционной функцией R₀(τ) соотношением

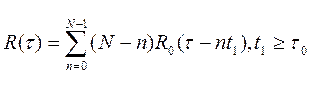, (8)

Воспользуемся выражением (8):

N=2 – количество импульсов

График АКФ представлен на рис.12

6.Спектральный анализ линейной цепи

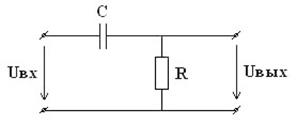
рис.13. Заданная схема цепи рис.14. Эквивалентная схема замещения

КЧХ определяется по следующей формуле:

Согласно эквивалентной схеме замещения:

;

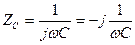По формуле делителя напряжения [5]:

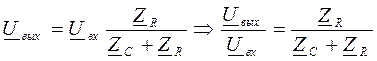
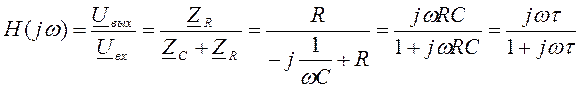
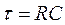– постоянная RC цепи [5].

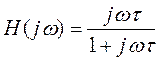
Определим АЧХ:

Определим ФЧХ:

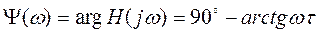
Определим значения H(ω) и Ψ(ω) на частотах ω=0 и ω= ,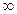

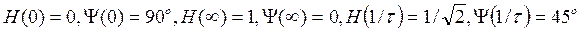
Графики АЧХ и ФЧХ приведены на рис.15

Аналитическое выражение для спектральной плотности сигнала на выходе цепи (рис.13), при воздействии в виде заданного сигнала S(t) (рис.1):

Амплитудный спектр сигнала на выходе цепи (рис.13), при воздействии в виде заданного сигнала S(t):

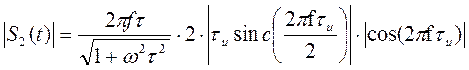
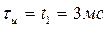
График амплитудного спектра сигнала на выходе цепи (рис.13) при воздействии в виде заданного сигнала S(t) представлен на рис.16

Список литературы.

1. Денисенко А.Н., Стеценко О.А. Теоретическая радиотехника: Справочное пособие ч.1: Детерминированные сигналы (методы анализа). – М.: Издательство стандартов, 1993. - 215с.

2. Денисенко А.Н., Стеценко О.А. Спектральный анализ сигналов: Учеб. пособие / Моск. ин-т радиотехники, электроники и автоматики.­– М., 1991. – 76 с.

3. Денисенко А.Н., Стеценко О.А. Линейные радиотехнические цепи: Учеб. пособие / Моск. ин-т радиотехники, электроники и автоматики. – М., 1992. – 78 с.

4. Нефёдов В.И. Основы радиоэлектроники и связи: Учебник для вузов –

2-е изд., перераб. и доп. – М.: Высш.шк., 2002. – 510 с.: ил.

5. Попов В.П. Основы теории цепей: Учеб. для вузов. – 3-е изд., испр.– М.: Высш. шк., 2000 – 575с.: ил.

6. Конспект лекций и семинарских занятий по курсу РТЦ и С.

7.Конспект лекций и семинарских занятий по курсу ОТЦ (2 курс).