Зависимые и независимые случайные величины
Случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какое значение принимает другая случайная величина.
Теорема. Для того чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы функция распределения системы 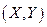 была равна произведению функций распределения составляющих:
была равна произведению функций распределения составляющих:
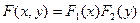 .
.
Аналогичную теорему можно сформулировать и для плотности распределения:
Теорема. Для того чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы плотность совместного распределения системы 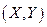 была равна произведению плотностей распределения составляющих:
была равна произведению плотностей распределения составляющих:
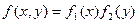 .
.
Определение. Корреляционным моментом 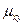 случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин:
случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин:
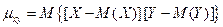 .
.
Практически используются формулы:
Для дискретных случайных величин: 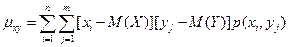 .
.
Для непрерывных случайных величин: 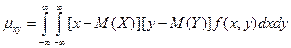 .
.
Корреляционный момент служит для того, чтобы охарактеризовать связь между случайными величинами. Если случайные величины независимы, то их корреляционный момент равен нулю.
Корреляционный момент имеет размерность, равную произведению размерностей случайных величин Х и Y. Этот факт является недостатком этой числовой характеристики, т.к. при различных единицах измерения получаются различные корреляционные моменты, что затрудняет сравнение корреляционных моментов различных случайных величин.
Для устранения этого недостаток применятся другая характеристика – коэффициент корреляции.
Определение.Коэффициентом корреляции  случайных величин Х и Y называется отношение корреляционного момента к произведению средних квадратических отклонений этих величин:
случайных величин Х и Y называется отношение корреляционного момента к произведению средних квадратических отклонений этих величин:
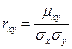 .
.
Коэффициент корреляции является безразмерной величиной. Коэффициент корреляции независимых случайных величин равен нулю.
Свойство. Абсолютная величина корреляционного момента двух случайных величин Х и Y не превышает среднего геометрического их дисперсий:
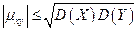 .
.
Свойство. Абсолютная величина коэффициента корреляции не превышает единицы:
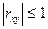 .
.
Случайные величины называются коррелированными, если их корреляционный момент отличен от нуля, и некоррелированными, если их корреляционный момент равен нулю.
Если случайные величины независимы, то они и некоррелированы, но из некоррелированности нельзя сделать вывод об их независимости.
Если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными.
Часто по заданной плотности распределения системы случайных величин можно определить зависимость или независимость этих величин.
Наряду с коэффициентом корреляции степень зависимости случайных величин можно охарактеризовать и другой величиной, которая называется коэффициентом ковариации. Коэффициент ковариации определяется формулой:
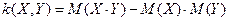 .
.
Пример. Задана плотность распределения системы случайных величин Х и Y:
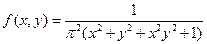 .
.
Определить, являются ли независимыми случайные величины Х и Y.
Для решения задачи преобразуем плотность распределения:
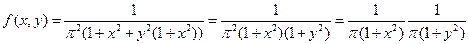 .
.
Таким образом, плотность распределения удалось представить в виде произведения двух функций, одна из которых зависит только от х, а другая – только от у, т.е. случайные величины Х и Y независимы. Очевидно, они также будут и некоррелированы.
