Определение скорости и ускорения точки при естественном способе задания движения

Из определения скорости точки

где

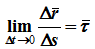
- единичный вектор касательной, тогда

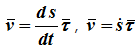
Алгебраическая скорость – это проекция вектора скорости на касательную, равная производной от дуговой координаты по времени. Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.

Из определения ускорения

поскольку τ - переменный по направлению вектор, то:

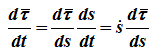
Производная

определяется только свойствами траектории в окрестности данной точки, при этом

n - единичный вектор главной нормали,

ρ - радиус кривизны траектории в данной точке.

Таким образом,

т.е. вектор ускорения раскладывается на две составляющие - касательное и нормальное ускорения:

Здесь:

- алгебраическое значение касательного ускорения (проекция вектора ускорения на касательную) характеризует изменение скорости по величине;

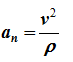
– нормальное ускорение (проекция вектора ускорения на главную нормаль) характеризует изменение скорости по направлению. Вектор ускорения всегда лежит в соприкасающейся плоскости и проекция ускорения на бинормаль равна нулю (a_b=0).

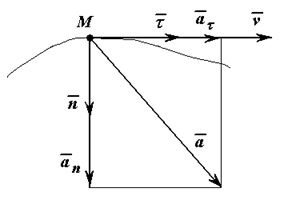
Движение точки ускоренное, если знаки проекций векторов скорости и ускорения на касательную совпадают.

Поступательное движение твёрдого тела.

Поступательное движение твердого тела

Поступательным называется такое движение твердого тела, при котором всякая прямая, проведенная в этом теле, остается параллельной своему начальному положению.

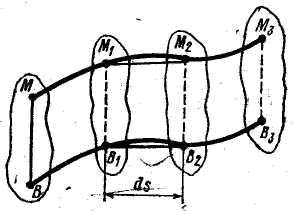
Проведенная в теле прямая ВМ во время движения перемещается параллельно своему начальному положению.

Рассмотрим перемещение тела за бесконечно малый промежуток времени dt. При этом можно считать, что точкиМ и Вперемещаются по прямолинейным и параллельным траекториям. За время dt они пройдут одинаковые пути ds. Следовательно, значения скорости этих точек будут одинаковы:

и направлены в одну сторону, т. е.

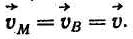
Аналогично доказывается равенство ускорений точек тела при поступательном движении:

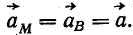
Следовательно, при поступательном движении тела все его точки описывают одинаковые траектории и в любой момент времени имеют равные по модулю и параллельно направленные скорости и ускорения.

Поступательное движение тела вполне характеризуется движением одной его точки, которое может быть задано координатным или естественным способом. Однако поступательное движение может совершать только твердое тело, а не отдельная точка. Примерами поступательного движения служат движение поршня двигателя, движение вагона на прямом участке пути и т. п. Поступательное движение может быть прямолинейным и криволинейным.