Методичні вказівки по виконанню завдання
1. Самостійно дати короткий опис роботи САК за принциповою схемою.
2. При вивченні конкретної САК її зручно попередньо формально розділити на типові елементи, виявити фізичні взаємозв'язки між цими елементами і відобразити їх в умовній формі на папері. Звичайно дослідження САК починають зі складання її функціональної схеми.
Для нашої системи функціональну схему можна представити у вигляді, наведеному на рис.1.8.
3. Складання диференціальних рівнянь окремих елементів САУ почнемо з рівняння генератора по каналу: 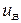 - вхід;
- вхід; 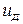 - вихід.
- вихід.
Скориставшись даними літературних джерел, можемо записати наступну систему рівнянь:
- рівняння електричної рівноваги ланцюга збудження (закон Кірхгофа)
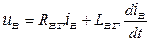 ;
;
- рівняння електричної рівноваги генератора
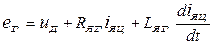 ;
;
- нелінійне рівняння характеристики холостого ходу генератора
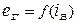 .
.
Спочатку приймемо допущення про те, що 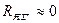 і
і 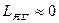 , тобто
, тобто 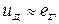 (зневажимо втратами напруги в якірній обмотці генератора).
(зневажимо втратами напруги в якірній обмотці генератора).
Введемо нові змінні: 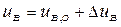 і
і 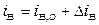 , де
, де 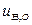 та
та 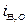 - значення відповідних змінних у точці стану рівноваги. Тоді
- значення відповідних змінних у точці стану рівноваги. Тоді
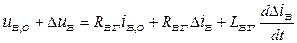 . (7.1)
. (7.1)
Віднявши з рівняння (7.1) рівняння рівноваги 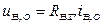 , одержимо наступне рівняння у відхиленнях:
, одержимо наступне рівняння у відхиленнях:
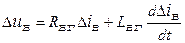 . (7.2)
. (7.2)
Далі зробимо лінеаризацію рівняння характеристики холостого ходу генератора на околицях точки рівноваги 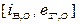 :
:
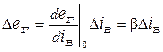 , (7.3)
, (7.3)
де 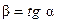 ;
; 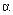 - кут нахилу дотичної до характеристики холостого ходу в точці рівноваги.
- кут нахилу дотичної до характеристики холостого ходу в точці рівноваги.
Підставивши 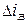 з (7.3) в 7.(2), одержимо:
з (7.3) в 7.(2), одержимо:
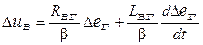 ,
,
або в стандартній формі і урахувавши, що ми прийняли 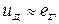 :
:
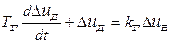 , (7.4)
, (7.4)
де: 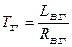 - постійна часу;
- постійна часу; 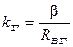 - передатний коефіцієнт генератора.
- передатний коефіцієнт генератора.
Відповідно до функціональної схеми складемо рівняння двигуна по каналу: 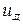 - вхід;
- вхід; 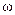 - вихід.
- вихід.
Для цього елемента, скориставшись даними літературних джерел, можемо записати наступну систему рівнянь:
- рівняння електричної рівноваги двигуна
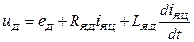 (7.5)
(7.5)
- рівняння руху привода
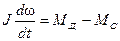 . (7.6)
. (7.6)
Тут: 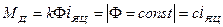 - обертальний момент, що розвиває двигун на валу;
- обертальний момент, що розвиває двигун на валу; 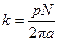 - конструктивний коефіцієнт;
- конструктивний коефіцієнт; 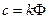 ;
; 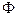 - магнітний потік;
- магнітний потік; 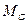 - момент опору навантаження, приведений до валу двигуна.
- момент опору навантаження, приведений до валу двигуна.
Рівняння (7.6) перепишемо у вигляді:
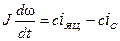 , де
, де 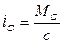 .
.
Звідки
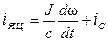 и.
и. 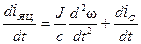
Підставимо два останніх співвідношення в рівняння (7.5) з урахуванням того, що 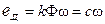 :
:
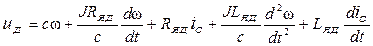 .
.
Перетворимо отримане рівняння до стандартного вигляду
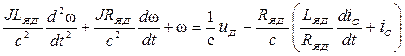 .
.
Введемо позначення:
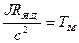 - електромеханічна постійна часу:
- електромеханічна постійна часу:
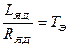 - електромагнітна постійна часу;
- електромагнітна постійна часу;
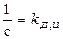 - передатний коефіцієнт двигуна по напрузі;
- передатний коефіцієнт двигуна по напрузі;
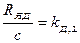 - передатний коефіцієнт двигуна по струму.
- передатний коефіцієнт двигуна по струму.
Тоді остаточно можемо записати:
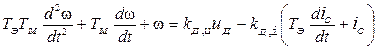 ,
,
або у відхиленнях
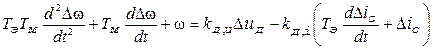 . (7.7)
. (7.7)
Таким чином, електродвигун можна представити математичною моделлю, що має два входи: 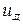 і
і 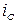 .
.
Рівняння напівпровідникового підсилювача по каналіу 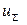 - вхід,
- вхід, 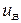 - вихід можна записати у вигляді:
- вихід можна записати у вигляді:
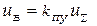 ,
,
де 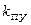 - передатний коефіцієнт.
- передатний коефіцієнт.
У відхиленнях це рівняння має схожий вигляд:
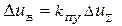 .
.
Рівняння тахогенератора по каналу 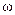 - вхід,
- вхід, 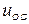 - вихід, зневажаючи динамікою процесів у ньому, запишемо у вигляді:
- вихід, зневажаючи динамікою процесів у ньому, запишемо у вигляді:
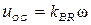 ,
,
де 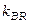 - передатний коефіцієнт.
- передатний коефіцієнт.
Або у відхиленнях:
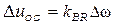 .
.
Рівняння замикання контуру у відхиленнях у нашому випадку записується як:
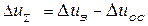 .
.
Надалі домовимося знак у рівняннях елементів не ставити, вважаючи всі змінні і їхні похідні малими відхиленнями від заданих значень. Тоді систему рівнянь САК можна представити в наступному вигляді
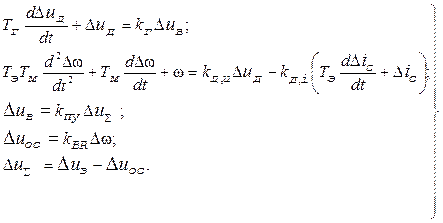 (7.8)
(7.8)
Для визначення передатних функцій елементів системи використаємо інтегральне перетворення Лапласа рівнянь елементів (7.8) при нульових початкових умовах:
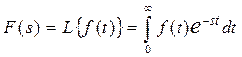 .
.
Одержимо наступну систему алгебраїчних рівнянь:
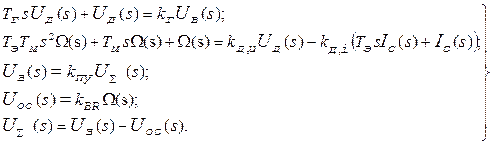 (7.9)
(7.9)
Передатною функцією елемента САК по визначенню називається відношення її вихідної величини до вхідної, перетворених по Лапласу при нульових початкових умовах. Тоді, скориставшись співвідношеннями (7.9), після перетворень одержимо:
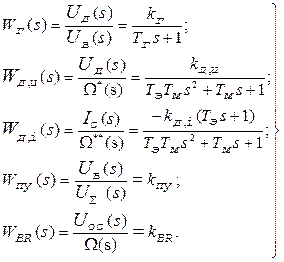 .
.
4. У нашому випадку, скориставшись знайденими передатними функціями ланок, структурну схему можна представити у вигляді, приведеному на рис. 7.1.
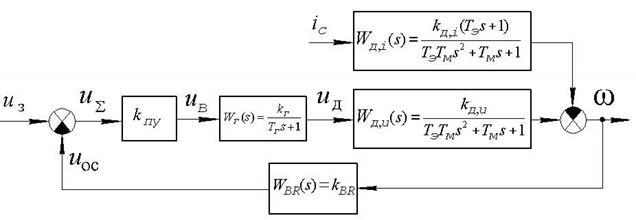
Рис. 7.1
Скориставшись останньою схемою, знайдемо передатну функцію системи по каналу завдання:
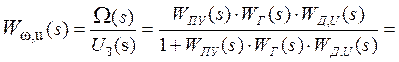
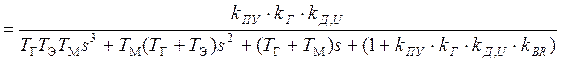 . (7.10)
. (7.10)
Відкіля можемо знайти характеристичне рівняння системи:
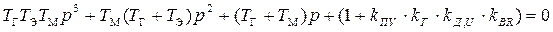 .(7.11)
.(7.11)
Значення передатного коефіцієнта напівпровідникового підсилювача 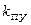 визначимо, скориставшись алгебраїчним критерієм стійкості Гурвіца.
визначимо, скориставшись алгебраїчним критерієм стійкості Гурвіца.
Для цього складемо головний визначник нашої системи
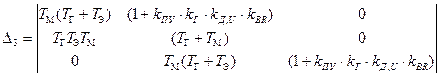 . (7.12)
. (7.12)
Звідси можна одержати визначник Гурвица 2-го порядку і зажадати, щоб він був більшим нуля:
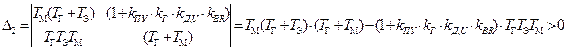 .(7.13)
.(7.13)
З нерівності (7.12) остаточно маємо:
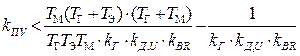 . (7.13)
. (7.13)
За остаточне значення 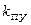 приймемо число, яке відповідає умові (7.13), а також забезпечує роботу двигуна зі швидкістю
приймемо число, яке відповідає умові (7.13), а також забезпечує роботу двигуна зі швидкістю 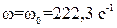 при рівні сигналу завдання
при рівні сигналу завдання 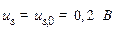 :
:
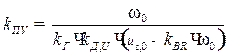 . (7.14)
. (7.14)
5. Для визначення перехідної характеристики системи вирішимо алгебраїчне рівняння (7.9) відносно 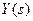 при заданому
при заданому 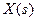 :
:
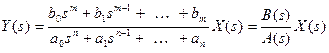 . (7.15)
. (7.15)
Визначимо оригінал рішення 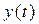 .
.
У загальному випадку для знаходження 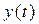 використовують зворотне перетворення Лапласа (
використовують зворотне перетворення Лапласа ( 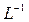 - перетворення), обумовлене формулою звертання Римана-Мелліна:
- перетворення), обумовлене формулою звертання Римана-Мелліна:
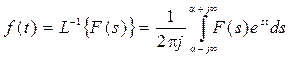 , (7.16)
, (7.16)
де 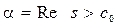 може бути будь-яким постійним числом
може бути будь-яким постійним числом 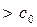 .
.
Найбільш простим методом є використання довідкових таблиць, у яких приводяться зображення 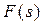 і відповідні їм оригінали
і відповідні їм оригінали 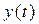 .
.
У випадку, якщо зображення є дрібно-раціональною функцією, тобто:
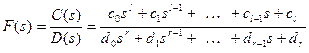 ,
,
причому 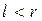 , а коефіцієнти
, а коефіцієнти 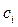 ,
, 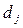 - дійсні числа, застосовується формула розкладання Хевісайда:
- дійсні числа, застосовується формула розкладання Хевісайда:
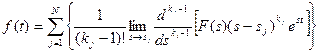 , (7.17)
, (7.17)
де 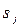 - корені рівняння
- корені рівняння 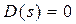 ;
; 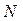 - число різних коренів;
- число різних коренів; 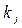 - кратність
- кратність 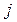 -го кореня.
-го кореня.
Диференціальні рівняння реальних САК мають звичайно прості корені 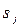 , і отже для них усі
, і отже для них усі 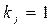 . Тоді вираз (7.17) з урахуванням співвідношення
. Тоді вираз (7.17) з урахуванням співвідношення
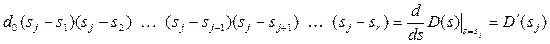
приймає більш простий вигляд
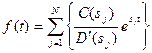 . (7.18)
. (7.18)
6. Навести криву перехідного процесу.
7. Зробити висновки.
Список літератури
1. Бесекерский В.А. Теория систем автоматического управления / В.А. Бесекерский, Е.П. Попов. М.: “Профессия”, 2004. 747с.
2. Зайцев Г.Ф. Теория автоматического управления и регулирования. 2-е издание перераб. и дополн. Киев: Высшая школа, 1988. 430с.
3. Иващенко Н.Н. Автоматическое регулирование. Теория и элементы систем. М.: Машиностроение, 1973. 606с.
4. Лукас В.А. Теория автоматического управления. М.: Недра, 1990. 416с.
5. Математические основы теории автоматического регулирования / под ред. Б.К. Чемоданова. М.: Высшая школа, 1971. 807с.
6. Мирошник И.В. Теория автоматического управления. Линейные системы. СПб: “Питер”, 2005. 333с.
7. Михайлов В.С. Теория управления. Учебное пособие для ВУЗов. Киев: Высшая школа, 1988. 309с.
8. Пантелеев А.В. Теория управления в примерах и задачах / А.В. Пантелеев, А.С. Бортаковский. М., Высшая школа, 2003. 583с.
9. Попов Е.П. Теория линейных систем автоматического регулирования и управления. М.: Наука, 1989. 496с.
10. Солодовников В.В. Основы теории и элементы систем автоматического регулирования / В.В. Солодовников, В.Н. Плотников, А.В. Яковлев. М.: Машиностроение, 1985. 536с.
11. Теория автоматического управления / под ред. А.В. Нетушила. М.: Высшая школа, 1972. 432с.
12. Теория автоматического управления. Учебное пособие / под ред. А.А. Воронова. Ч.1. М.: Высшая школа, 1987. 367с.
13. Филипс Ч. Системы управления с обратной связью / Ч. Филипс, Р. Харбор. М.: Лаборатория базовых знаний, 2001. 616с.
Зміст
Передмова...……………......…………………………………………......3
1. Основні поняття ТАК...…………..........…………………………......4
2. Математичний опис САК...….……………….……......…………......13
3. Характеристики САК...…………………………………………......26
4. Типові ланки САК і їхні характеристики...........………………......35
5. Стійкість САК.........……………………......……………………......38
6. Якість САК...………………......…………………………………......45
7. Індивідуальне завдання...……………………………………………52
Список літератури...…………………..……………………………......62
Навчальне видання
