Случайная величина, которая может принимать лишь конечное или счётное число значений, называется дискретной

Случайные величины будем обозначать буквами греческого алфавита: x (кси), h (эта), ¼ Значения случайной величины будем записывать в виде конечной или бесконечной последовательности x₁, x₂,¼, x_n,¼

Если говорится, что задана случайная величина x, это значит, что каждому исходу w_k случайного эксперимента поставлено в соответствие единственное число x_k, что записывается в виде равенства x_k = x(w_k).

Некоторые из значений x_k могут совпадать, то есть различным исходам w может соответствовать одно и то же число x. Если все значения случайной величины совпадают, то будем говорить, что случайная величина постоянна.

Пусть А_k — множество всех элементарных исходов, каждому из которых соответствует значение x_k (k = 1,2,¼,n) случайной величины x. Этот факт можно записать в виде формулы

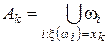
Таким образом, А_k – это событие (строго говоря, это верно лишь в случае конечного или счётного числа исходов). Для каждого события А_k определим число р_k ³ 0, равное вероятности этого события: р_k = P(A_k). Очевидно, что

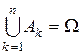, A_i∩A_j = Æ (i,j = 1,2,¼,n, i¹j), .

Теперь каждому значению x_k случайной величины x можно поставить в соответствие вероятность р_k = P(A_k) события А_k. Если такое соответствие определено то будем говорить, что задан закон распределения диск­ретной случайной величины x. Обычно закон распределения диск­ретной случайной величины представляется в виде таблицы

x	х1	х2	х3	¼	хn	(1)
P	p1	p2	p3	¼	pn

В дальнейшем для краткости будем называть величину p_i вероятностью значения х_i случайной величины. Отметим, что закон распределения содержит всю информацию о случайной величине, и задать случайную величину можно, просто представив её закон распределения.

Задача.

Стрелок стреляет в мишень два раза. Известно, что он попадает в мишень с первого выстрела с вероятностью 0,1. Если первый выстрел удачный, то при втором выстреле он попадает в мишень с вероятностью 0,7, если же первый выстрел неудачный, то при втором выстреле он попадает в мишень с вероятностью 0,5.

Написать закон распределения случайной величины x – числа попаданий в мишень.

Решение.

Очевидно, случайная величина может принимать значения 0, 1, 2. Значение 0 случайная величина может принимать при наступлении следующего события: стрелок не попадает в мишень с первого выстрела (событие А) и не попадает в мишень со второго выстрела (событие В). По формуле умножения вероятностей

Р(А∩В) = Р(А)Р(В/А)

В нашем случае Р(АÇВ) = 0,9×0,5 = 0,45.

Значение 1 случайная величина может принимать в двух случаях: первый выстрел – промах (событие С), второй выстрел – попадание (событие D) или первый выстрел – попадание (событие E), второй выстрел – промах(событие F).

Р(С∩D) = 0,9×0,5 = 0,45; Р(EÇF) = 0,1×0,3 = 0,03

Таким образом, вероятность, с которой случайная величина принимает значение 1 равна 0,48.

Значение 2 случайная величина принимает с вероятностью, равной 0,1×0,7 = 0,07. Искомый закон распределения случайной величины имеет вид