Тема: «Решение уравнений и систем уравнений».

Нестандартные задачи для учащихся 10 – 11 классов».

Под нестандартными задачами будем понимать задачи, которые традиционными методами и преобразованиями не решаются. Они, как правило, в варианте бывают последними и могут быть условно названы задачами «на пятёрку».

Отмечу то, что, несмотря на нестандартность, такие задачи не выходят за рамки школьной программы, поскольку могут быть решены школьными методами. Другое дело, что бывает крайне трудно за ограниченное время найти решение.

Каждый год придумывают задачи, решение которых требует принципиально нового подхода, так что исчерпать все типы таких задач просто невозможно. Зато возможно набраться опыта в решении подобных задач и, по крайней мере, не впадать в панику, если вдруг такая задача попадётся на экзамене. Изучим некоторые методы, которые помогут если не решить, то хотя бы упростить задачу. Методы следующие: метод мажорант, функционально-графический метод, метод удачной подстановки или группировки, геометрический подход.

Тема: «Использование свойств элементарных функций при решении уравнений и неравенств».

Цель:

проверка, оценка и коррекция знаний, умений и навыков учащихся, связанных с числовыми функциями, графиками функций, преобразованиями графиков, элементарным исследованием функций (чётность, нечётность, периодичность, монотонность, промежутки знакопостоянства функции, точки экстремума).

Проверка знания учащимися фактического материала, умения объяснять сущность основных понятий осуществляется в процессе беседы с последующим выполнением заданий.

Задание №1.

Функция f(x) определена на всей числовой прямой, является нечётной, периодической с периодом 4 и на промежутке 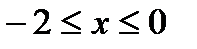её значения вычисляются по правилу . Решить уравнение .

Решение:

Известно, что:

1. D(f)=R.
2. f(x)=- f(-x) на D(f), f(x)-нечётная функция.
3. T=4, f(x)-периодическая функция.
4. При В силу нечётности функции f(x), она задаётся на отрезке формулой Построив график данной функции на отрезке , продолжим его на всю числовую ось, используя то, что функция f(x) – периодическая, с периодом 4.

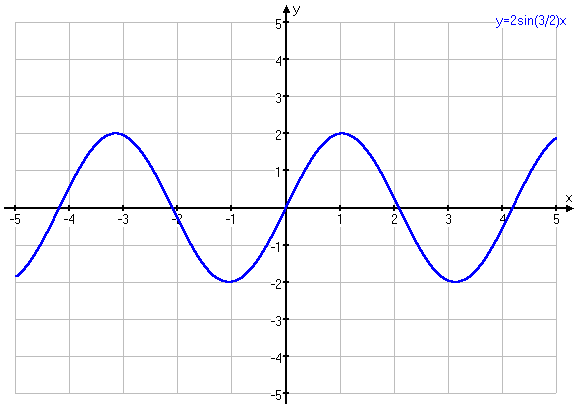
Теперь перейдём к решению уравнения.

Область допустимых значений уравнения: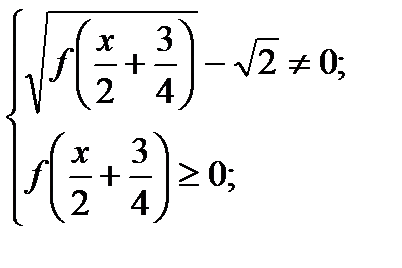

.

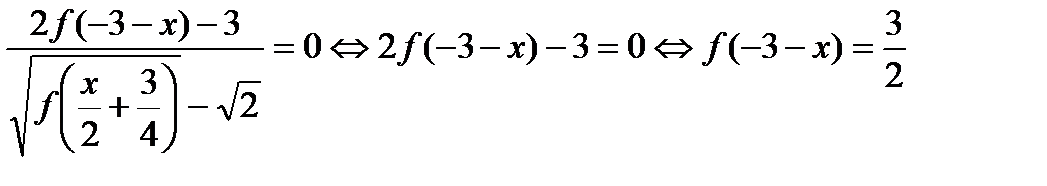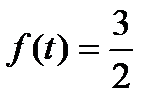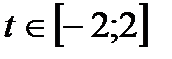Обозначим и решим уравнение при . Так как при , то можно считать, что . Тогда или 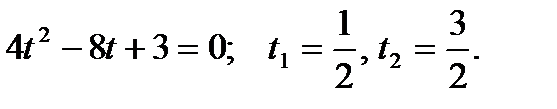В силу периодичности с периодом T=4 общие решения имеют вид

Теперь можно найти х :

Проверим, входят ли эти решения в ОДЗ. Для этого решим второе неравенство и для найденных значений х проверим выполнение первого условия системы.

Для первой серии решений имеем 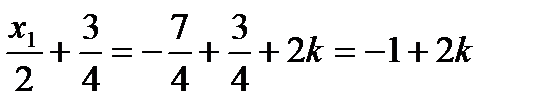. Из второго неравенства следует, что 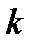- нечётно, т.е. 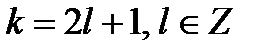, но 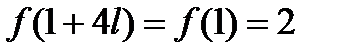, т.е. первая серия не входит в ОДЗ. Аналогичные рассуждения проводим для второй серии решений, здесь получаем , и убеждаемся, что эта серия входит в ОДЗ. С учётом второго неравенства, получаем, что и , причём 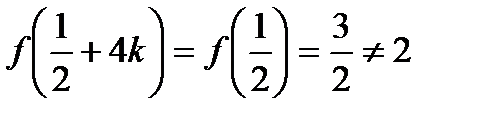. Легко найти .

Ответ: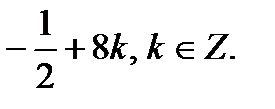

Задание №2.

Функция f(x) определена на всей числовой прямой, является нечётной, периодической с периодом 4 и на промежутке 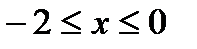её значения вычисляются по правилу . Решить уравнение .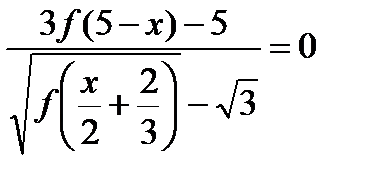

Ответ: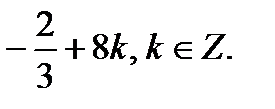

Задание №3.

Функция определена на всей числовой прямой, является нечётной, периодической с периодом 4 и на промежутке её значения вычисляются по правилу Решить уравнение

Ответ:

Задание №4.

Покажите, что функции и взаимно обратные, и решите уравнение .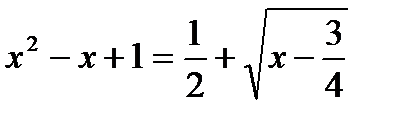

Решение:

функция 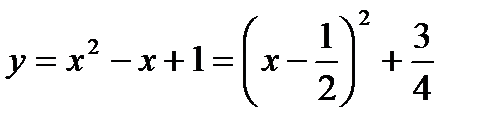возрастает при , причём, при изменении в указанном промежутке . Следовательно, в промежутке 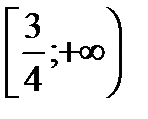определена обратная функция (согласно теореме о существовании обратной функции) , которая находится из уравнения 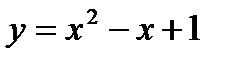. Решая уравнение относительно , получаем . Заменяя х на у и у на х, получим , что и требовалось доказать.

Решим уравнение 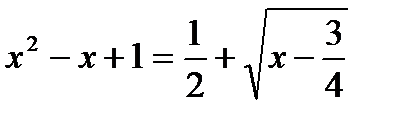. Так как графики прямой и обратной функций могут пересекаться только на прямой 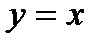, то решая уравнение , находим .

Задание №5.

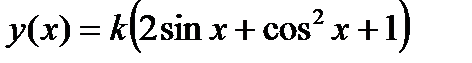Найти все числа для которых функция не принимает значений, больших 3.

Ответ: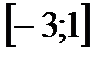

Решение:

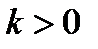Рассмотрим функцию Требование для всех х: а) при означает 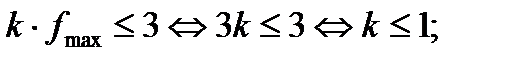б) при выполняется автоматически; в) при 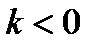равносильно требованию для всех х то есть Собираем полученные значения вместе: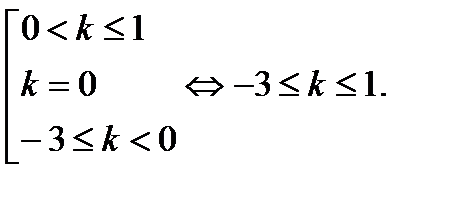

Задание №6.

Известно, что Найти

Ответ: .

Решение: 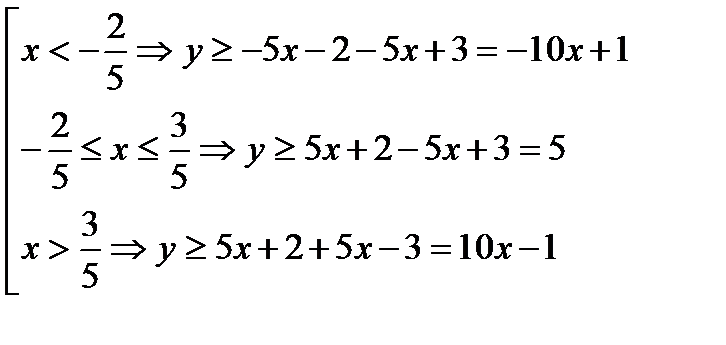, построив данную совокупность, легко видеть, что минимум х+у достигается в точке с координатами 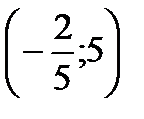. Следовательно, .

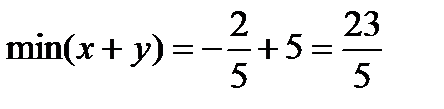Задание №7. Известно, что . Найти .

Ответ: 12.

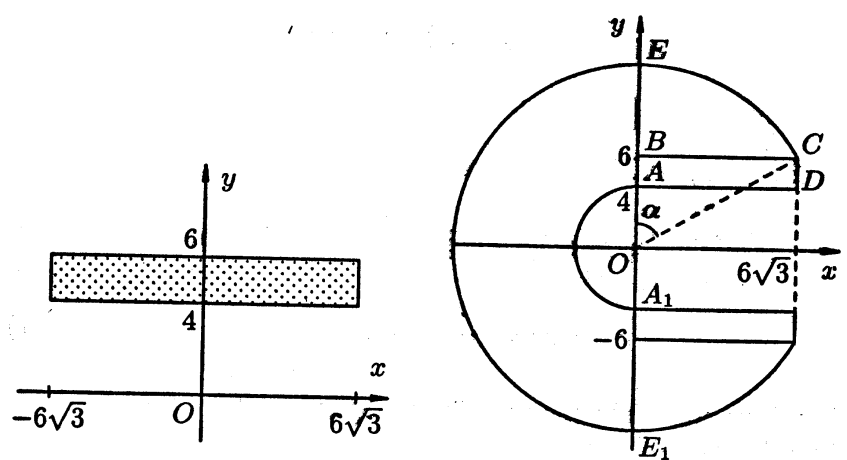
Задание №8.Множество точек, рас положенных внутри фигуры F, задано на координатной плоскости условием 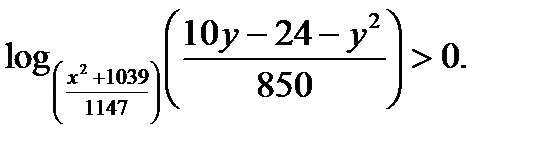Множества F(t) получаются из F поворотом вокруг начала координат против часовой стрелки на угол t . Найти площадь фигуры, образованной точками, каждая из которых при некотором принадлежит множеству F(t).

Ответ:

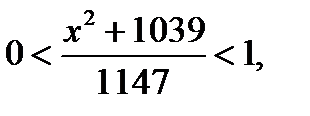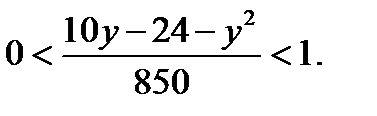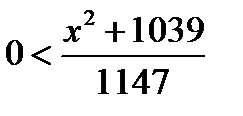Решение: Определим сначала вид фигуры F . Рассмотрим два случая. 1) Если основание логарифма меньше 1, то есть то должно выполняться двойное неравенство Так как то неравенство справедливо для всех действительных х. Решим неравенство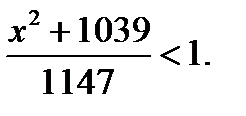 Неравенство выполняется при а неравенство выполняется при всех действительных у ,поскольку 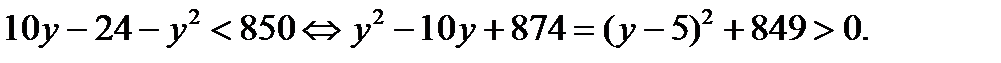2) должно быть 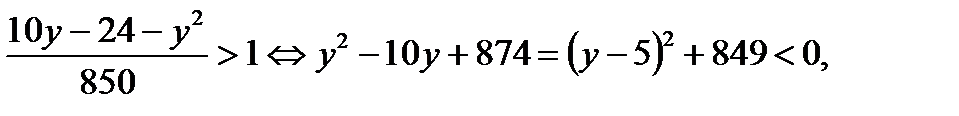что невозможно. Итак, во втором случае решений нет.

Мы получили, что множество решений данного неравенства совпадает с внутренностью прямоугольника, ограниченного прямыми 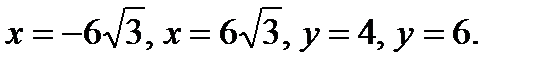В процессе вращения против часовой стрелки вокруг начала координат на угол прямоугольник «заметает» фигуру, изображённую на рисунке.

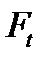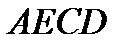Другими словами, эта фигура представляет собой объединение множеств при . Её площадь можно найти как сумму площади полукольца и удвоенной площади фигуры Итак, Площадь фигуры равна сумме площадей полусегмента и прямоугольника Найдём площадь полусегмента 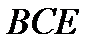: Далее, Окончательно получаем

Задание №9.Множество точек, расположенных внутри фигуры G, задано на координатной плоскости условием 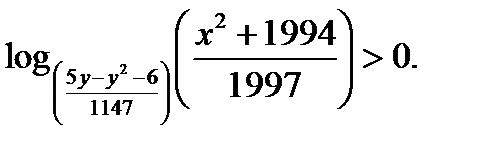Множества G(t) получаются из G поворотом вокруг начала координат против часовой стрелки на угол t . Найти площадь фигуры, образованной точками, каждая из которых при некотором принадлежит множеству G(t).

Ответ: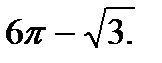

Задание №10.

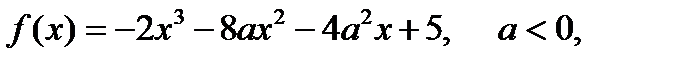График функции ; где и прямая 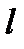, заданная уравнением 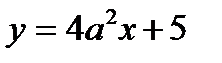, имеют ровно две общие точки. 1) Найдите а, если площадь фигуры, ограниченная графиком функции и прямой 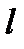, равна . 2) Рассматриваются прямые, каждая из которых касается графика функции в точке с положительной абсциссой. Среди этих прямых выбрана та, которая пересекает ось в точке с наименьшей ординатой. Найти эту ординату.

Ответ:

Задание №11.

График функции ; где и прямая 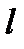, заданная уравнением 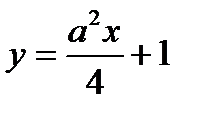, имеют ровно две общие точки. 1) Найдите а, если площадь фигуры, ограниченная графиком функции и прямой 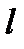, равна 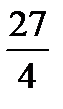. 2) Рассматриваются прямые, каждая из которых касается графика функции в точке с положительной абсциссой. Среди этих прямых выбрана та, которая пересекает ось 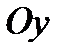в точке с наибольшей ординатой. Найти эту ординату.

Ответ: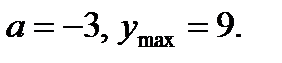

Задание №12.

Найти наибольшее и наименьшее значения функции .

Решение:

Введем обозначения . Поскольку 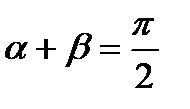, то .

Наименьшее значение данной функции соответствует наибольшему значению произведения 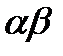. Так как , то наибольшее значение 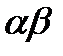необходимо искать при . В этом случае 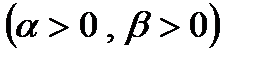можно записать, что .

Наибольшее значение 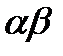достигается при . Следовательно, наименьшее значение исходной функции достигается при и равно .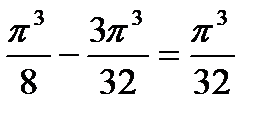

Наименьшее значение произведения 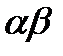, где , достигается при условии, что 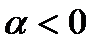, причем необходимо, чтобы абсолютные величины 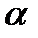и были наибольшими. При будет . Именно в этой точке произведение 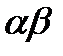достигает минимума, так как 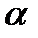принимает минимальное, а - максимальное из возможных значений. Итак, при исходная функция имеет наибольшее значение .

Ответ: .

Задание №13.

Найти область определения функции .

Решение:

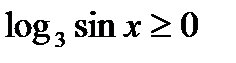С одной стороны, , так как , а с другой стороны , так как стоит под знаком квадратного корня. Остаётся одна возможность: .

Ответ: .

Задание №14.

Найти область определения функции .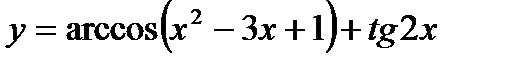

Решение:

Чтобы существовал , необходимо и достаточно, чтобы 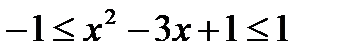, то есть .

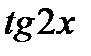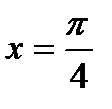Из найденных интервалов нужно исключить точки, в которых не существует, то есть числа вида . Два из этих чисел: и 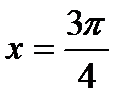лежат в найденных интервалах.

Ответ:

Задание №15.

Доказать, что функция 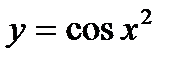не является периодической.

Решение:

найдем корни функции

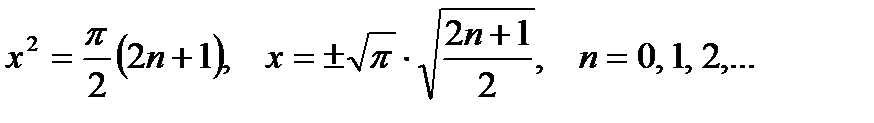
Рассмотрим положительные корни .

Предположим, что 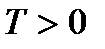- период функции. Тогда, если при функция равна нулю, то и при 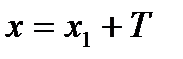она тоже равна нулю, то есть . Аналогично 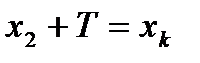. Вычитая одно равенство из другого, получим , то есть . Возведем в квадрат: . После вторичного возведения в квадрат получим .

Это равенство возможно лишь при 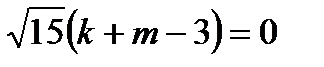, так как все остальные его элементы – целые.

Однако числа 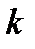и 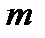выбраны так, что и 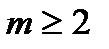, то есть .

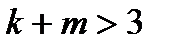Что и требовалось доказать.

Тема: «Решение уравнений и систем уравнений».

Задание №16.

Сколько решений системы уравнений 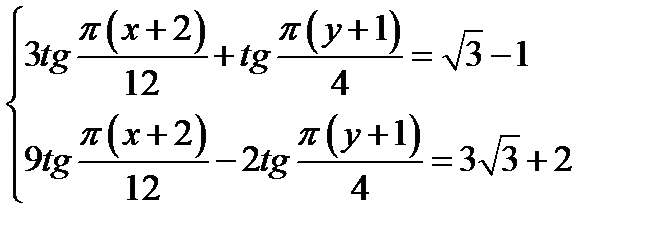удовлетворяют условию ?

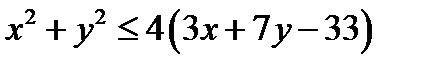Ответ: 10 решений.

Задание №17.

Сколько решений системы уравнений 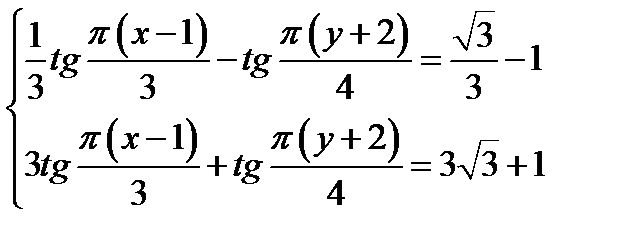удовлетворяют условию ?

Ответ: 3 решения.

Решение:

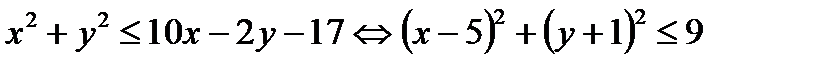- круг, с центром 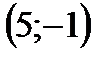и радиусом 3 . Отсюда . Построив данный круг и отметив точки, перебирая n и k,убеждаемся, что три решения системы уравнений удовлетворяют плоскости круга.

Задание №18.

Решить уравнение .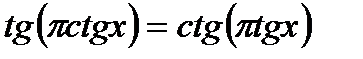

Решение:

ОДЗ:

.

;

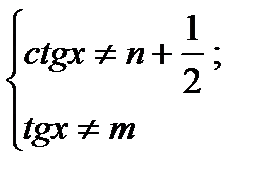
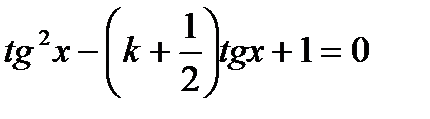, таккак и не являютсякорнями

Теперь необходимо исключить целые k, лежащие в промежутке Заметим, что если одна из частей данного уравнения обращается в бесконечность, то и вторая должна быть бесконечностью, то есть достаточно проверить, чтобы 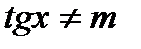, где . Чтобы k было целым, необходимо, чтобы . При этом получаем .

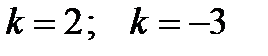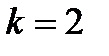• ; (не подходит),
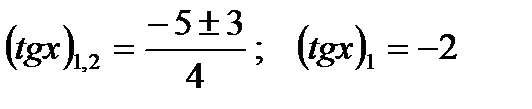• ; (не подходит) .

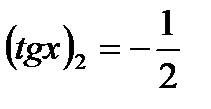Ответ: ;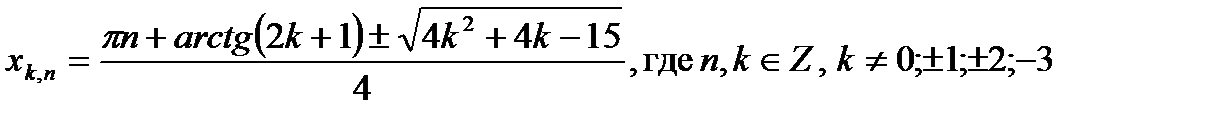

.

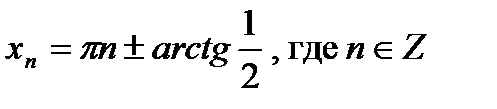Задание№19.

Решить уравнение

Ответ: