Образец выполнения задания № 2
Маршрут движения коммивояжера
Коммивояжеру необходимо посетить три города по одному разу и вернуться в исходный город. Каков должен быть маршрут поездки, чтобы затраты на дорогу были минимальны? Данные о тарифах на проезд представлены в виде матрицы чисел (таблица 2.1).
Таблица 2.1
Тарифы на проезд

Решение:
Математическая модель задачи.
Определим булевы переменные задачи: xij = 1, если коммивояжер переезжает из города i в город j, и xij = 0, если коммивояжер не переезжает из города i в город j.
Тогда задача заключается в определении минимума целевой функции
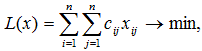
при ограничениях:
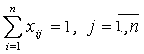 | – только один въезд в город j, |
 | – только один выезд из города i. |
В задаче коммивояжера необходимо еще одно условие, а именно:
ui – uj + (n – 1)xij ≤ n – 2, i ≠ j, i, j = 2,…, n.
Это специальное условие обеспечивает устранение нескольких несвязанных между собой маршрутов и циклов, попросту означающих перемещение коммивояжера по замкнутому частичному маршруту.
Вид электронной таблицы для решения задачи.
1. В ячейки В11:D13 вводим матрицу тарифов.
2. Вводим формулы
| Ячейка | Формула | Примечание |
| В7 | =СУММ(В4:В6) | Копируем в диапазон В7:D7 |
| E4 | =СУММ(В4:D4) | Копируем в диапазон E4:E6 |
| B15 | =СУММПРОИЗВ(B4:D6;B11:D13) | Целевая функция |
| D15 | =B4+C5+D6 | Исключение пути i → i |
| В19 | =$C$8–C8+2*C5 | Копируем в диапазон В19:C19 |
| В20 | =$D$8–C8+2*C6 | Копируем в диапазон В20:C20 |
3. Исходные данные приведены на рис.2.1.
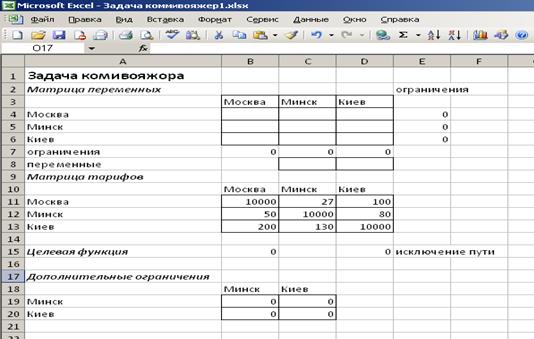
Рис. 2.1. Исходные данные задачи
4. Сценарий решения:
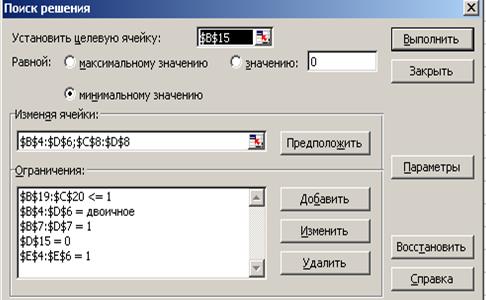
Рис.2.2. Окно Поиск решения
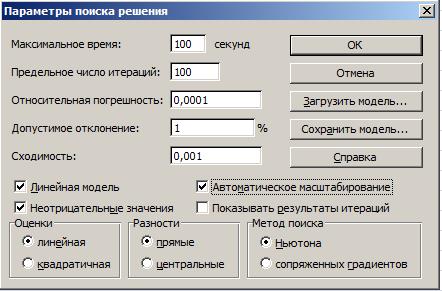
Рис. 2.3. Параметры Поиска решения
5. Он приводит к следующим результатам:
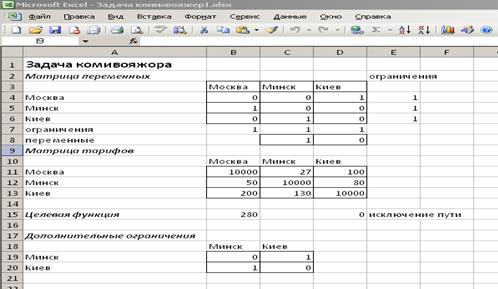
Рис. 2.4. Результаты решения задачи коммивояжера
6. Ответ: маршрут 1→3→2→1. Стоимость проезда 280.
Список литературы
Основная литература
1. Бережная Е.В., Бережной В.И. Математические методы и моделирование экономических систем: учеб. пособие. – М.: Финансы и статистика, 2005.
2. Глухов В.В. и др. Математические методы и модели для менеджмента. – СПб.: Изд-во «Лань». 2007.
3. Гусева Е.Н. Экономико-математическое моделирование: учеб. пособие. – Ростов-на-Дону: Флинта; МПСИ, 2011
4. Кочович Е. Финансовая математика: с задачами и решениями. – М.: Финансы и статистика, 2004.
5. Мур Д. и др. Экономическое моделирование в MSExcel. – М.: Издательский дом «Вильямс», 2004.
6. Орлова И.В. Экономико-математические методы и модели: компьютерное моделирование. – М.: Вузовский учебник, 2009.
7. Самаров К.Л. Экономико-математические модели: учебно-метод. пособие. – М.: ООО «Резольвента», 2009
Дополнительная литература
8. Гончаров В.А. Методы оптимизации. Учебное пособие для вузов. - Издательство: Юрайт, Высшее образование, 2010г.
9. Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: Учеб. пособ. - 2-е изд., испрб. и доп. – М.: Вузовский учебник: ИНФРА-М, 2010.
10. Гарнаев А.Ю. Excel, VBA, Internet в экономике и финансах: – СПб.: БХВ, 2005.
11. Рудикова Л.В. Microsoft Excel Для студента. – СПб.: БХВ, 2007.
