Тест Лукаса-Лемера для чисел Мерсенна
Вход: Число Мерсенна Mn=2n—1.
Ш.1. Пробными делениями проверить, имеет ли n делители между «2» и 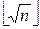 . Если имеет, идти на Выход с сообщением «Mn – составное число».
. Если имеет, идти на Выход с сообщением «Mn – составное число».
Ш.2. Задать u=4.
Ш.3. n—2 раза вычислить u=(u2—2) mod Mn.
Ш.4. Если u=0, то «Mn – простое число», иначе «Mn – составное число».
Выход.
В настоящее время особое внимание уделяется двойным числам Мерсенна MMp=2Mp –1, например 7=M3=MM2. Алгоритм построения таких чисел следующий: сначала строится сравнительно небольшое простое число Мерсенна Mp, а затем по нему – двойное число Мерсенна MMp, которое проверяется на простоту тестом Лукаса-Лемера минуя первый шаг.
Аналогично строятся тройные и т.д. числа Мерсенна. Например, тройным числом Мерсенна является 127=M7=MMM2.
Не для всех чисел Мерсенна существуют двойные и тройные числа. Например, MM13 не является простым.
Первыми простыми числами Мерсенна являются M2=3, M3=7, M5=31, M7=127, M13=8191, M17, M19, M31.
На данный момент (2007 г.) не доказана конечность или бесконечность количества простых чисел Мерсенна.
Теорема Диемитко и процедура генерации простых чисел заданной длины ГОСТ Р 34.10-94.
Следующая теорема позволяет строить доказуемо простые числа большего размера на основе простых чисел меньшего размера.
Теорема Диемитко.
Пусть n=qR+1, где q – простое число, R – четное, R<4(q+1).
Если найдется a<n: 1) an—1≡1(mod n); 2) 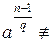 1(mod n), то n – простое число.
1(mod n), то n – простое число.
■
Итак, если имеем простое число q, то, перебирая четные числа R, строим числа n=qR+1 и испытываем их на простоту согласно теореме Диемитко, пока не получим простое число. По полученному числу можно построить еще одно простое число и т.д.
Приведем алгоритм перехода от меньшего простого числа q: |q|= 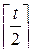 к большему p: |p|=t, использующийся в ГОСТе. Фигурирующая в процедуре ξ есть равномерно распределенная на (0,1) случайная величина, получаемая с помощью линейного конгруэнтного генератора. Каждый раз на Шаге 1 получают новое значение ξ.
к большему p: |p|=t, использующийся в ГОСТе. Фигурирующая в процедуре ξ есть равномерно распределенная на (0,1) случайная величина, получаемая с помощью линейного конгруэнтного генератора. Каждый раз на Шаге 1 получают новое значение ξ.
Алгоритм перехода от меньшего простого числа к большему:
Вход: t – требуемая размерность простого числа, q – простое число : |q|= 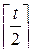 .
.
Ш.1. Вычисляем N= 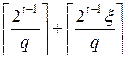 . Если N – нечетное, то N=N+1.
. Если N – нечетное, то N=N+1.
Ш.2. u=0.
Ш.3. Вычисляем p=(N+u)q+1 – кандидат в простые.
Ш.4. Если p>2t, возвращаемся на Ш.1.
Ш.5. Если 2n—1≡1(mod n) и 2N+u 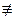 1(mod n), то идем на Выход.
1(mod n), то идем на Выход.
Ш.6. Вычисляем u=u+2. Возвращаемся на Ш.3.
Выход. p – простое число.
Первое слагаемое в построении числа N обеспечивает минимальный требуемый размер числа p, а второе вносит в процедуру поиска новых простых чисел необходимый элемент случайности.
Проверка на Шаге 4 необходима, чтобы число p не превышало своей верхней границы, а проверка на Шаге 5 есть проверка условия теоремы Диемитко при a=2.
Пример:
Вход: t=4, q=3=[11]2
1. N= 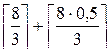 =3. N=N+1=4.
=3. N=N+1=4.
2. u=0.
3. p=4·3+1=13.
4. 13<24=16.
5. 212 mod 13 =1, 24 mod 13 = 3.
Выход. р=13=[1011]2
Замечание
Поскольку на Шаге 5 условие теоремы Диемитко проверяется не для всех a<p, а только для 2, то некоторые простые числа, сгенерированных этим алгоритмом, не опознаются как простые. Но вероятность того, что для простого числа n наугад выбранное число a будет удовлетворять условиям теоремы Диемитко, есть (1—1/q), а q – достаточно большое число. Таким образом, проверки при a=2 вполне достаточно, чтобы не отсеивать слишком много простых чисел. Выбор a=2 обусловлен тем, что возведение числа 2 в степень в двоичном представлении является простой операцией.
