Нелинейное программирование

Задачи с линейной целевой функцией и нелинейной системой

Ограничений

Задача 2.1.1. На множестве решений системы неравенств

ìx 2 + y 2 £ 36,

ï

í x ³ 0,

î

ï y ³ 0.

найти глобальные экстремумы функции z=2x+y.

Решение. На рисунке 8 множество допустимых решений заштриховано. Это множество выпукло. Линиями уровня функции z=2x+y являются параллельные прямые с угловым коэффициентом К = -2. Очевидно, что глобальный минимум до- стигается в точке О (0; 0), а глобальный максимум - в точке А касания прямой уровня и окружности x2+y2=36. Найдем координаты точки A. Для этого достаточно составить уравнение прямой и решить систему, состоящую из уравнения прямой и уравнения окружности. Заметим, что прямая перпендикулярна линии уровня, а, следовательно, ее угловой коэффициент К1 равен ½ (K1K = -1). Прямая l проходит

через точку О и имеет угловой коэффициент

ìx 2 + y 2 = 36

K = 1 .

1 2

Поэтому ее уравнение таково:

y = 1 x. Решая систему

ï

í

ï y =

î

1 x,

2

получаем:

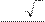x = 12 × 5 ,

y = 6 × 5 .

y Итак, глобальный минимум, равный

0, достигается в точке О(0;0), а глобаль-

ный максимум, равный

l

6 5 ,- в точке

А(2,4×

5 ; 1,2

5). Локальных экстрему-

A мов, отличных от глобальных, функция не достигает.

0 x

рис.8

Задача 2.1.2. Найти глобальные экстремумы функции стве решений системы неравенств

z = x - y - 5

на множе-

ï

ì(x- 1)y £ 1

ïx + y ³ 3,5

í

ï0 £ x £ 5

ïî0 £ y £ 5.

Решение. Множество допустимых решений состоит их двух отдельных частей, каждая из которых выпукла (рис. 9). Вычислим значение целевой функции

z = x - y - 5

в точках A, B, C, D, K, N, M,

L, предварительно найдя их координа-

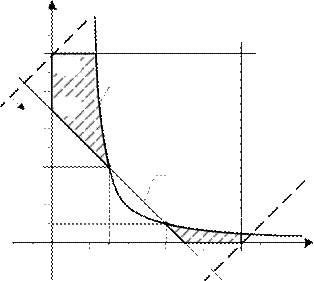
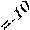y ты:

N

M (x-1)y=1

y=5

A(5;0), B(5; 1 ), C(3;

4

1 ), D(3,5;0),

2

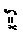4 K(1 1 ;2), L(0;3,5), N(1 1 ;5), M(0;5).

L

K

2 x+y=3,5

Z = - 1 ,

B 4

ZC= -2,5,

ZD= -1,5,

C

1 рис.9

B

A

0

ZK= -5,5, ZL= -8,5,

ZM = -10.

ZN= -8,8,

ZA = 0,

1 2 3 D 4

5 6 x

Итак, глобальный максимум до- стигается в точке (5;0) и равен 0, а гло-

бальный минимум- в точке (0;5) и равен -10.

Нетрудно видеть, что в точке С функция достигает локального минимума, равного -2,5, который отличен от глобального (значение целевой функции в точке С меньше, чем значение ее в соседних вершинах B и D ). Аналогично, в точке K достигается локальный максимум, отличный от глобального.

Задача 2.1.3. Дана целевая функция ограничений

z = x1+ x2(max; min) и нелинейная система

ì4x1+ 3x2£ 24,

ï

ï

í(x1- 2)(x2+ 1) ³ 4,

îx1³ 0, x2³ 0.

Решение. Изобразим на плоскости

X10X 2

( X 0Y )

множество решений системы

ограничений. Построим линию, соответствующую уравнению

Запишем это уравнение в виде:

(x1 - 2)(x2 +1) = 4 .

x2= -1 +

4 .

x1- 2

Графиком этой функции является гипербола, уравнения ее асимптот:

x1= 2; x2= -1.

В первой части первого неравенства удовлетворяют все точки, которые распо- ложены не ниже построенной ветви гиперболы. Второму неравенству системы

ограничений

(4x1+ 3x2£ 24)

удовлетворяют все

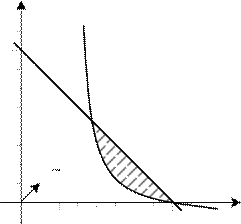x2 точки, которые расположены под прямой

4x1+ 3x2£ 24

или на этой прямой. Таким обра-

1 n

рис.10

0 1 2 3 4 5 6 7 8 9 x1

зом, множеством решений системы ограниче- ний является множество точек, заштрихованное на рис. 10.

Линиями уровня является прямые

x1+ x2= z0(z0- const). Нормалью к этим прямым

является вектор

nr = (1;1) .

Если передвигать линии уровня в направлении нормали, то значение

z0будет

увеличиваться, а если передвигать эти линии в противоположном направлении, то

z0 будет уменьшаться.

1) наибольшее значение функции цели будет достигаться в точке А, являю-

щейся точкой пересечения прямой и гиперболы. Найдем координаты точки А:

ì(x1 - 2)(x2+ 1)= 4,

í

î4x1 + 3x2= 24.

Выразим из первого уравнения x2

ï 2

ìx

и подставим его во второе уравнение:

= 6 - x1,

ï x1- 2

í

Отсюда, получаем систему:

ï4x

ïî 1

+ 3 6 - x1

x1- 2

= 24.

x

ï 2

ì = 6 - x1

í x1- 2

ï 2

î4x1

- 35x1 + 66 = 0.

Решением этой системы являются две пары чисел:

æ

ç х1=

è

; x2=

и

13ö

÷

3 ø

1 2 ç

(x = 6; x = 0). Координаты точки А æ 11;

è 4

÷ , при этом

13ö

3 ø

zmax

= 11

4

+ 13

3

= 85 .

12

2) минимальное значение функции цели будет достигаться в точке В, в кото-

рой линии уровня

x1+ x2= z0

совпадает с касательной к гиперболе.

Запишем линию уровня в виде:

x2 = -x1 + z0, отсюда следует, что угловой ко-

эффициент касательной к гиперболе в точке В равен -1. Значит, производная в точ- ке касания равна -1:

' æ 6 - x1ö 1

x2 = çç

÷÷ = - .

Отсюда, имеем:

è x1-1 ø

(x1

- 2)2

x1= 4

= 1; (x1

или

- 2)2= 4;

x1= 0 .

Значение

x1= 0

принадлежит другой ветви параболы и, поэтому, является по-

сторонним решением.

Координаты точки В(4;1), при этом

zmin

= 4 +1 = 5 .

Задача 2.1.4. Дана линейная целевая функция ограничений

z = x1+ 3x2и нелинейная система

ì(x1

- 5)2+ (x

- 3)2³ 9,

ï

ï(x

- 5)2+ (x

- 3)2£ 36,

í 1 2

ï

ïx1 + x2 ³ 8

îx1³ 0; x2³ 0.

Найти глобальные экстремумы.

Решение. Изобразим на плоскости

X10X 2

( X 0Y )

область допустимых решений

системы ограничения задачи. Множеством решений первых двух неравенств:

(x1

(x

- 5)2+ (x

- 5)2+ (x

- 3)2 ³ 9,

- 3)2 £ 36.

1 2

является область (кольцо), заключенная между двумя окружностями и с общими

центром в точке С(5;3) и радиусом

R1= 3 и

R2= 6 . Множеством решений неравен-

ства

x1+ x2³ 8 является плоскость, расположенная над прямой

x1+ x2= 8 . Область

допустимых решений системы ограничений на рис. 11 выделена штриховкой. Ли-

нии уровня функции цели - прямые

x1+ 3x2= z0(z0- const) . Нормаль к этим прямым -

есть вектор

nr = (1;3). Перемещаем линию уровня в направлении нормали до тех пор,

пока она не станет касательной к верхней окружности.

Обозначим точку касания буквой D; в этой точке значение Z будет макси- мальным. Угловой коэффициент касательной К равен коэффициенту прямой

x1+ 3x2= z0. значит,

k = - .

3

С другой стороны, угловой коэффициент касательной для окружности

(x1

- 5)2+ (x

- 3)2 = 36

найдем, дифференцируя это уравнение по переменной

x1:

2(x1

x2

- 5) + 2(x2

- 3) × x' = 0

Отсюда,

9 D

' x1- 5 .

x

=

x2 - 3

6 Решим систему уравнений:

4 ì x1- 5 1

x

3 ï-

í 2

2 ï

= - ,

- 3 3

2 2

1 n î(x1- 5)

+ (x2- 3)

= 36;

-1 1 2

3 4 5 6 7 8

9 10 x1

ìx2= 3x1 - 12,

í

î 1

(x - 5)2+ (3x

-2

- 15)2= 36;

ìx2= 3x1 - 12,

í 2

рис.11

î5x1

- 50x1+ 107 = 0.

Одно решение этой системы

x = 25 - 3

1 5

10 ; x

= 15 - 9 10

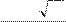5

является посторонним,

потому, что

x2не удовлетворяет условию неотрицательности.

Другое решение

x = 25 + 3

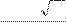
1 5

10» 6.9; x

= 15 + 9

5

10» 8.7

дает координаты точки D.

При этом

zmax

= x1

+ 3x2

= 70 + 30

5

10= 14 + 6

10 .

Для определения минимального значения функции цели будем перемещать

линию уровня в направлении, противоположном вектору нормали nr , до тех пор, пока у нее не окажется одна общая точка с областью допустимых решений. Такой

точкой является точка Е=(8;0). Значит,

Zmin = 8 , если

x1= 8; x2= 0.