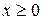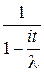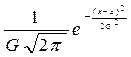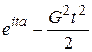Пусть μ—число успехов в n независимых испытаниях Бернулли с вероятностью успеха р в одном испытании, тогда 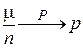 .
.
Введем случайные величины μi—число успехов в i-ом испытании. Тогда 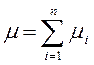 .
.
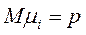 ,
, 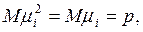 (т.к.
(т.к. 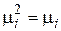 ).
).
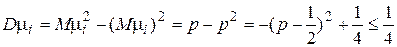 (т.е. дисперсия ограничена
(т.е. дисперсия ограничена 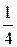 ).
).
μ1, μ2,…, μn—независимы. По закону больших чисел в форме Чебышёва 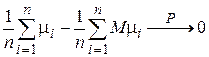 .
.
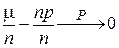 .
.
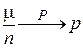 .
.
В чем смысл закона больших чисел в форме Бернулли?
Пусть в результате эксперимента может произойти или не произойти событие А. P(A)—вероятность события А в одном эксперименте. Эксперимент повторяется N раз, N(A)—число появлений события А в этих N экспериментах.
b2,…, bn2, n3 элементов k-ой группы x1, x2,…, xnk можно составить ровно n1∙ n2∙…∙nk различных упорядоченных комбинаций вида 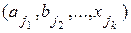 , содержащих по одному элементу из каждой группы. 1. При k=2 утверждение выполняется (Лемма 1). 2. Предположим, что Лемма 2 выполняется для k. Докажем для k+1 группы элементов , содержащих по одному элементу из каждой группы. 1. При k=2 утверждение выполняется (Лемма 1). 2. Предположим, что Лемма 2 выполняется для k. Докажем для k+1 группы элементов 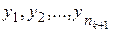 . Рассмотрим комбинацию . Рассмотрим комбинацию 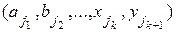 как как 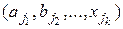 и и 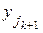 . Предположение дает возможность вычислить число комбинаций из k элементов, их n1 n2 nk. По Лемме 1 число комбинаций из k+1 элементов n1 n2… nk+1. Пример. При бросании двух игральных костей N=6∙6=36. При бросании трех костей N=6∙6∙6=216. Леммы 1 и 2 называются основными правилами комбинаторики. Пусть имеется множество из n элементов a1, a2 ,an. Будем рассматривать выборку объема k . Предположение дает возможность вычислить число комбинаций из k элементов, их n1 n2 nk. По Лемме 1 число комбинаций из k+1 элементов n1 n2… nk+1. Пример. При бросании двух игральных костей N=6∙6=36. При бросании трех костей N=6∙6∙6=216. Леммы 1 и 2 называются основными правилами комбинаторики. Пусть имеется множество из n элементов a1, a2 ,an. Будем рассматривать выборку объема k 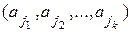 из n элементов. Все выборки можно классифицировать по 2 признакам: 1. упорядоченные и неупорядоченные. 2. с возвращением и без возращения. Если выборка упорядоченная, то выборки с одним и тем же составом выбранных элементов, но разным порядком элементов в выборках, считаются различными. Если выборка считается неупорядоченной, то все выборки с одним и тем же составом элементов из n элементов. Все выборки можно классифицировать по 2 признакам: 1. упорядоченные и неупорядоченные. 2. с возвращением и без возращения. Если выборка упорядоченная, то выборки с одним и тем же составом выбранных элементов, но разным порядком элементов в выборках, считаются различными. Если выборка считается неупорядоченной, то все выборки с одним и тем же составом элементов | |
Чебышёва: Для 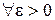 . . 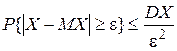 . . 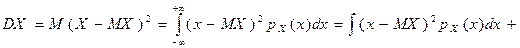 {x││x-MX│≥ε} {x││x-MX│≥ε}  {x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε} 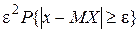 . Таким образом, . Таким образом, 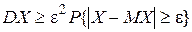 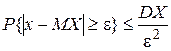 . Теорема 2. (закон больших чисел в форме Чебышёва). Пусть Х1,Х2,…—последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной, т.е. . Теорема 2. (закон больших чисел в форме Чебышёва). Пусть Х1,Х2,…—последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной, т.е. 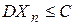 . Тогда эта последовательность удовлетворяет закону больших чисел. Обозначим через . Тогда эта последовательность удовлетворяет закону больших чисел. Обозначим через 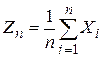 . Нужно доказать, что . Нужно доказать, что 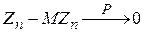 . . 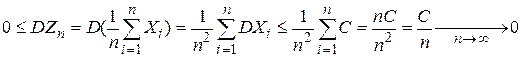 . . | |
отождествляются. Пример. Возьмем множество из трех элементов {1,2,3}. Выбираем k=2. | (1,1);(1,2);(1,3); (2,1);(2,2);(2,3); (3,1);(3,2);(3,3); | (1,1);(1,2);(1,3); (2,2);(2,3); (3,3); | С возвращением | | (1,2);(1,3); (2,1);(2,3); (3,1);(3,2); | (1,2);(1,3); (2,3); | Без возвращения | | упорядоченная | неупорядоченная | выборка |
Составим общую таблицу числа выборок: 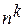 | 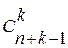 | С возвращением | 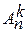 | 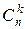 | Без возвращения | | упорядоченная | Неупорядоченная | Выборка | Упорядоченная выборка с возвращением 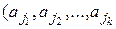 ). Каждый элемент выборки может принимать n значений, т.е. число выборок ). Каждый элемент выборки может принимать n значений, т.е. число выборок 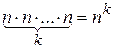 . Упорядоченная выборка без возвращения . Упорядоченная выборка без возвращения 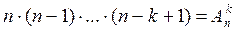 . . o Упорядоченная выборка без возвращения называется размещением. Число размещений 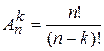 . . Пример. В лифт 12-этажного дома зашли 3 человека. Найти вероятность того, что все вышли на разных этажах. 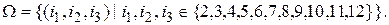 | |
Свойство 3.данных случайных величин равна произведению характеристических функций этих случайных величин, т.е. 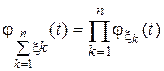 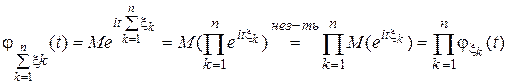 . Свойство 4.Если М . Свойство 4.Если М 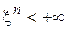 , характеристическая функция случайной величины , характеристическая функция случайной величины 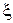 n раз дифференцируема, причем n раз дифференцируема, причем 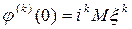 , где , где 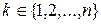 . Замечание. Необходимо отметить, что функция распределения величины однозначно определяется характеристической функцией. Таким образом, характеристическая функция является законом распределения случайной величины. § 24. Законы больших чисел. 0. 1Последовательность случайных величин Х1, Х2,… называется сходящейся по вероятности к случайной величине Х, если для любого положительного числа . Замечание. Необходимо отметить, что функция распределения величины однозначно определяется характеристической функцией. Таким образом, характеристическая функция является законом распределения случайной величины. § 24. Законы больших чисел. 0. 1Последовательность случайных величин Х1, Х2,… называется сходящейся по вероятности к случайной величине Х, если для любого положительного числа 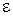 , т.е. , т.е. 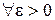 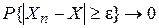 при при 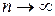 . Обозначается . Обозначается 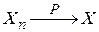 . 0. 2 Говорят, что последовательность случайных величин Х1, Х2,… удовлетворяют закону больших чисел, если . 0. 2 Говорят, что последовательность случайных величин Х1, Х2,… удовлетворяют закону больших чисел, если 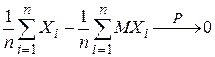 . Теорема 1. Для любой случайной величины Х, имеющей конечную дисперсию DX, справедливо неравенство . Теорема 1. Для любой случайной величины Х, имеющей конечную дисперсию DX, справедливо неравенство | |
n=113. 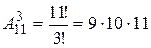 , , 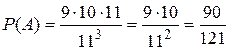 . o Перестановкой из k элементов называется совокупность этих же элементов, записанных в произвольном порядке. Pk-число перестановок из k элементов. . o Перестановкой из k элементов называется совокупность этих же элементов, записанных в произвольном порядке. Pk-число перестановок из k элементов. 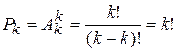 , поскольку 0!=1. o Произвольное k-элементное подмножество множества n элементов называется сочетанием из n элементов по k элементов. Сочетание—это неупорядоченная выборка объема k из n элементов. Обозначается число всех сочетаний из n элементов по k элементов через , поскольку 0!=1. o Произвольное k-элементное подмножество множества n элементов называется сочетанием из n элементов по k элементов. Сочетание—это неупорядоченная выборка объема k из n элементов. Обозначается число всех сочетаний из n элементов по k элементов через 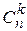 . .  . . 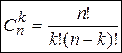 , где , где 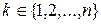 . . 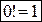 . Свойства сочетаний: 1. . Свойства сочетаний: 1. 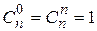 . 2. . 2. 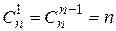 . 3. . 3. 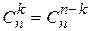 . 4. . 4. 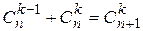 . . | |
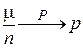 .
.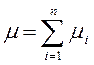 .
.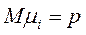 ,
, 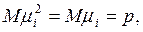 (т.к.
(т.к. 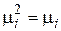 ).
).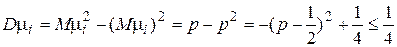 (т.е. дисперсия ограничена
(т.е. дисперсия ограничена 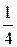 ).
).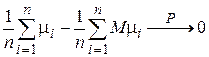 .
.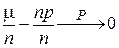 .
.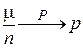 .
.
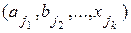 , содержащих по одному элементу из каждой группы. 1. При k=2 утверждение выполняется (Лемма 1). 2. Предположим, что Лемма 2 выполняется для k. Докажем для k+1 группы элементов
, содержащих по одному элементу из каждой группы. 1. При k=2 утверждение выполняется (Лемма 1). 2. Предположим, что Лемма 2 выполняется для k. Докажем для k+1 группы элементов 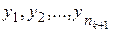 . Рассмотрим комбинацию
. Рассмотрим комбинацию 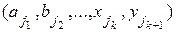 как
как 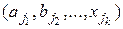 и
и 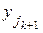 . Предположение дает возможность вычислить число комбинаций из k элементов, их n1 n2 nk. По Лемме 1 число комбинаций из k+1 элементов n1 n2… nk+1. Пример. При бросании двух игральных костей N=6∙6=36. При бросании трех костей N=6∙6∙6=216. Леммы 1 и 2 называются основными правилами комбинаторики. Пусть имеется множество из n элементов a1, a2 ,an. Будем рассматривать выборку объема k
. Предположение дает возможность вычислить число комбинаций из k элементов, их n1 n2 nk. По Лемме 1 число комбинаций из k+1 элементов n1 n2… nk+1. Пример. При бросании двух игральных костей N=6∙6=36. При бросании трех костей N=6∙6∙6=216. Леммы 1 и 2 называются основными правилами комбинаторики. Пусть имеется множество из n элементов a1, a2 ,an. Будем рассматривать выборку объема k 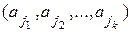 из n элементов. Все выборки можно классифицировать по 2 признакам: 1. упорядоченные и неупорядоченные. 2. с возвращением и без возращения. Если выборка упорядоченная, то выборки с одним и тем же составом выбранных элементов, но разным порядком элементов в выборках, считаются различными. Если выборка считается неупорядоченной, то все выборки с одним и тем же составом элементов
из n элементов. Все выборки можно классифицировать по 2 признакам: 1. упорядоченные и неупорядоченные. 2. с возвращением и без возращения. Если выборка упорядоченная, то выборки с одним и тем же составом выбранных элементов, но разным порядком элементов в выборках, считаются различными. Если выборка считается неупорядоченной, то все выборки с одним и тем же составом элементов 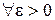 .
. 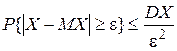 .
. 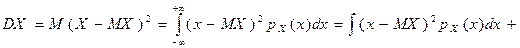 {x││x-MX│≥ε}
{x││x-MX│≥ε}  {x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε}
{x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε} {x││x-MX│≥ε} 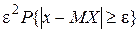 . Таким образом,
. Таким образом, 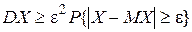
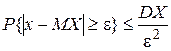 . Теорема 2. (закон больших чисел в форме Чебышёва). Пусть Х1,Х2,…—последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной, т.е.
. Теорема 2. (закон больших чисел в форме Чебышёва). Пусть Х1,Х2,…—последовательность попарно независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной, т.е. 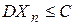 . Тогда эта последовательность удовлетворяет закону больших чисел. Обозначим через
. Тогда эта последовательность удовлетворяет закону больших чисел. Обозначим через 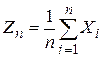 . Нужно доказать, что
. Нужно доказать, что 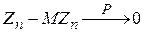 .
. 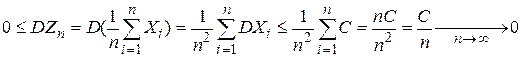 .
. 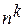
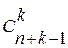
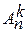
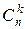
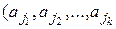 ). Каждый элемент выборки может принимать n значений, т.е. число выборок
). Каждый элемент выборки может принимать n значений, т.е. число выборок 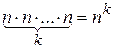 . Упорядоченная выборка без возвращения
. Упорядоченная выборка без возвращения 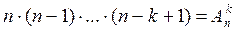 .
.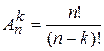 .
.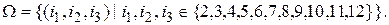
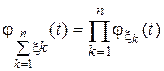
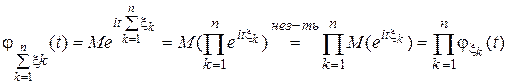 . Свойство 4.Если М
. Свойство 4.Если М 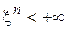 , характеристическая функция случайной величины
, характеристическая функция случайной величины 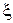 n раз дифференцируема, причем
n раз дифференцируема, причем 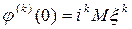 , где
, где 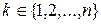 . Замечание. Необходимо отметить, что функция распределения величины однозначно определяется характеристической функцией. Таким образом, характеристическая функция является законом распределения случайной величины. § 24. Законы больших чисел. 0. 1Последовательность случайных величин Х1, Х2,… называется сходящейся по вероятности к случайной величине Х, если для любого положительного числа
. Замечание. Необходимо отметить, что функция распределения величины однозначно определяется характеристической функцией. Таким образом, характеристическая функция является законом распределения случайной величины. § 24. Законы больших чисел. 0. 1Последовательность случайных величин Х1, Х2,… называется сходящейся по вероятности к случайной величине Х, если для любого положительного числа 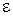 , т.е.
, т.е. 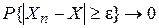 при
при 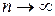 . Обозначается
. Обозначается 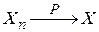 . 0. 2 Говорят, что последовательность случайных величин Х1, Х2,… удовлетворяют закону больших чисел, если
. 0. 2 Говорят, что последовательность случайных величин Х1, Х2,… удовлетворяют закону больших чисел, если 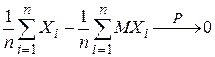 . Теорема 1. Для любой случайной величины Х, имеющей конечную дисперсию DX, справедливо неравенство
. Теорема 1. Для любой случайной величины Х, имеющей конечную дисперсию DX, справедливо неравенство 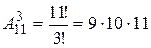 ,
, 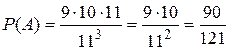 . o Перестановкой из k элементов называется совокупность этих же элементов, записанных в произвольном порядке. Pk-число перестановок из k элементов.
. o Перестановкой из k элементов называется совокупность этих же элементов, записанных в произвольном порядке. Pk-число перестановок из k элементов. 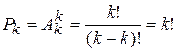 , поскольку 0!=1. o Произвольное k-элементное подмножество множества n элементов называется сочетанием из n элементов по k элементов. Сочетание—это неупорядоченная выборка объема k из n элементов. Обозначается число всех сочетаний из n элементов по k элементов через
, поскольку 0!=1. o Произвольное k-элементное подмножество множества n элементов называется сочетанием из n элементов по k элементов. Сочетание—это неупорядоченная выборка объема k из n элементов. Обозначается число всех сочетаний из n элементов по k элементов через 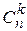 .
.  .
. 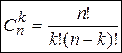 , где
, где 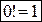 . Свойства сочетаний: 1.
. Свойства сочетаний: 1. 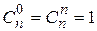 . 2.
. 2. 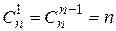 . 3.
. 3. 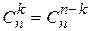 . 4.
. 4. 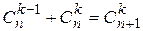 .
. 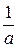 ,
, 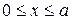
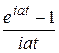
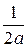 ,
, 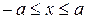
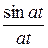
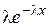 ,
,