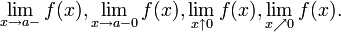Расстояние от точки до плоскости
· Пусть плоскость П задана уравнением AX+BY+CZ+D=0 и дана точка M0(X0;Y0;Z0) . Тогда расстояниеp от точки M0 до плоскости П определяется по формуле
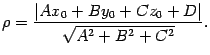 |
Доказательство. Расстояние от точки M0 до плоскости  -- это, по определению, длина перпендикуляра
-- это, по определению, длина перпендикуляра  , опущенного из точки на плоскость
, опущенного из точки на плоскость 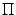 .
.  Рис.11.9.Расстояние от точки до плоскости
Рис.11.9.Расстояние от точки до плоскости
Вектор KM0 и нормальный вектор n плоскости 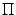 параллельны, то есть угол
параллельны, то есть угол 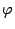 между ними равен 0 или
между ними равен 0 или 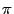 , если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому
, если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому
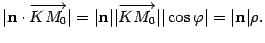
Откуда
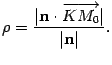 |
Координаты точки  , которые нам неизвестны, обозначим X1,Y1,Z1 . Тогда
, которые нам неизвестны, обозначим X1,Y1,Z1 . Тогда  . Так как
. Так как 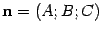 , то
, то 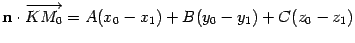 . Раскрыв скобки и перегруппировав слагаемые, получим
. Раскрыв скобки и перегруппировав слагаемые, получим
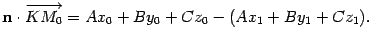 | (11.9) |
Точка  лежит на плоскости
лежит на плоскости 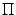 , поэтому ее координаты удовлетворяют уравнению плоскости:
, поэтому ее координаты удовлетворяют уравнению плоскости: 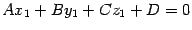 . Отсюда находим, что
. Отсюда находим, что 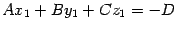 . Подставив полученный результат в формулу (11.9), получим
. Подставив полученный результат в формулу (11.9), получим 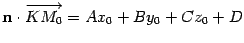 . Так как
. Так как 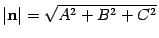 , то из формулы (11.8) следует формула (11.7).
, то из формулы (11.8) следует формула (11.7).
12. Е- окрестности точки и символов +и- бесконечности. Понятие предела функции в точке и на бесконечности. Бесконечно малые и бесконечно большие функции.
ε-окре́стность множества в функциональном анализе и смежных дисциплинах — это такое множество, каждая точка которого удалена от данного множества менее, чем на ε.
Определения
§ Пусть 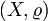 есть метрическое пространство,
есть метрическое пространство, 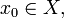 и ε > 0. ε-окрестностью x0 называется множество
и ε > 0. ε-окрестностью x0 называется множество
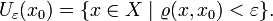
§ Пусть дано подмножество 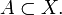 Тогда ε-окрестностью этого множества называется множество
Тогда ε-окрестностью этого множества называется множество
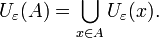
Замечания
§ ε-окрестностью точки x0 таким образом называется открытый шар с центром в x0 и радиусом ε.
§ Прямо из определения следует, что
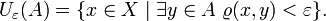
§ ε-окрестность является окрестностью и, в частности, открытым множеством.
[Примеры
Пусть есть вещественная прямая 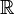 со стандартной метрикой
со стандартной метрикой 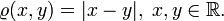 Тогда
Тогда
§ U2(1) = ( − 1,3);
§ U1([5,7]) = (4,8).
Пределы функций.
Определим понятие окрестности точки х0 как множество значений х, являющихся решениями неравенства 0<|x - x0| < δ, где δ > 0 — некоторое число. Само значение х0 может включаться в окрестность или не включаться в нее (в этом случае окрестность называется проколотой).
Пусть функция у = f(x) определена в некоторой окрестности точки х0.
Определение 13.7. Число А называется пределом функции у = f(x) при х, стремящемся к х0, если такое, что |f(x) - A| < ε при |x - x0| < δ.
ОКРЕСТНОСТЬЮ ТОЧКИ Хо называется любой интервал, содержащий эту точку.
ПРОКОЛОТОЙ ОКРЕСТНОСТЬЮ т. Хо называется окрестность т. Хо, из которой выброшена сама точка.
ОКРЕСТНОСТЬЮ "+" БЕСКОНЕЧНОСТИ называется любой полубесконечный промежуток вида (а;+) .
ОКРЕСТНОСТЬЮ "-" БЕСКОНЕЧНОСТИ называется любой полубесконечный промежуток вида (- ;b) .
ОКРЕСТНОСТЬЮ БЕСКОНЕЧНОСТИ называется объединение двух любых окрестностей + и - . Функция f(х) называется бесконечно малой в окрестности т. Хо, если для любого числа >0 существует проколотая окр. т. Хо такая, что для любого числа Х, принадлежащего прокол. окр. т. Хо выполняется неравенство іf(х) і<. >0 U U => іf(x) і< Число А называется пределом ф-ции f(х) в т. Хо, если в некоторой прок. окр. этой точки ф-цию f(х) можно представить в виде f(х) =А+ (х) , где (х) -бесконечно малое в окрестности т. Хо. limf(x) =А Ф-ция f(х) называется непрерывной в т. Хо, если в некоторой окр. т. Хо эту ф-цию можно представить в виде: f(х) =f(х) + (х) , где (х) -б. м. в окр. т. Хо.
Иными словами, f(х) -непрерывна в т. Хо, если она в этой точке имеет предел и он равен значению ф-ции.
ТЕОРЕМА: Все элементарные ф-ции непрерывны в каждой точке области определения.
Схема: 1. ф-я элементарна 2. определена 3. непрерывна 4. предел равен значению ф-ции 5. значение ф-ции равно 0 6. можно представить в виде б. м.
СВОЙСТВА БЕСКОНЕЧНО МАЛЫХ:
Теорема#1: Единственная константа, явл-ся б. м. Теорема#2: Если (х) и (х) -б. м. в окр. т. Хо, то их сумма тоже б. м. в этой окр.
Ф-ция f(х) называется ограниченной в окр. т. Хо, если сущ.
проколотая окр. т. Хо и сущ. число М>0, такие что іf(х) і<М в каждой точке прок. окр. т. Хо.
U M>0: іf(x) і Теорема#3: Если (х) -б. м. в окр. т. Хо, то она ограничена в этой окр.
Теорема#4: О произведении б. м. на ограниченную: Если ф-ция (х) -б. м., а f(х) -ограниченная в окр. т. Хо, то (х) *f(х) -б. м. в окр. т. Хо.
Теорема#5: О промежуточной б. м.: Если (х) и (х) -б. м. в окр. т. Хо и (х) < (х) < (х) - 2 в окр. т. Хо U, то (х) -б. м. в окр. т. Хо. Две б. м. называются сравнимыми, если существует предел их отношения. Б. м. (х) и (х) в окр. т. Хо называются одного порядка, если предел их отношений есть число не равное 0.
Две б. м. в окр. т. Хо называются эквивалентными, если предел их отношения равен 1.
Теорема#1: Если и -эквивалентные б. м., то их разность есть б. м. более высокого порядка, чем и чем.
Теорема#2: Если разность двух б. м. есть б. м. более высокого порядка, чем и чем, то и есть
эквивалентные б. м.
Пределы на бесконечности
Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим (по абсолютной величине).
Определения, аналогичное "ε−δ"
§ Пусть задана числовая функция с неограниченной сверху областью определения, то есть f:M⊂R→R, и supM=∞. Число A∈R называется пределом функции f при x→+∞(предел в плюс-бесконечности), если
∀ε>0∃T∈R∀x∈M∩(T,∞)|f(x)−A|<ε.
Пишут:
limx→∞f(x)=A.
§ Аналогично пусть f:M⊂R→R, и infM=∞. Число A∈R называется пределом функции f при x→−∞ (предел в минус-бесконечности), если
∀ε>0∃T∈R∀x∈M∩(−∞,T)|f(x)−A|<ε.
Пишут:
- limx→−∞f(x)=A.
13. Полуокресности, односторонние пределы. Графическая иллюстрация.
Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственнолевосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (или преде́лом спра́ва).
Определения
Пусть задана числовая функция 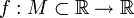 и
и 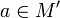 — предельная точка области определения M.
— предельная точка области определения M.
§ Число 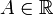 называется правосторонним пределом функции f при x стремящемся к a, если
называется правосторонним пределом функции f при x стремящемся к a, если 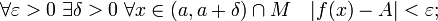
§ Число 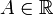 называется левосторонним пределом функции f при x стремящемся к a, если
называется левосторонним пределом функции f при x стремящемся к a, если
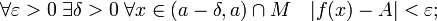
Обозначения
§ Правосторонний предел принято обозначать любым из нижеследующих способов:
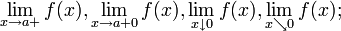
§ Аналогичным образом для левосторонних пределов приняты обозначения: