Лабораторная работа м 8

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТРЕНИЯ КАЧЕНИЯ

Цель работы:

– экспериментальная проверка зависимостей между физическими величинами, характеризующими колебания установки;

– экспериментальное определение коэффициента трения качения.

Приборы и принадлежности:

– установка для определения коэффициента трения качения, 3 пары съёмных направляющих из различного материала, конструкция из сплошных цилиндров, съёмные магниты.

Описание установки

Рисунок 1 – Общий вид установки

Общий вид установки показан на рисунке 1. На основании (1) крепится пара съёмных направляющих (2), на которые устанавливается конструкция из сплошных цилиндров (3). Конструкция может быть выведена из положения равновесия на заданный угол и может совершать колебания.

На установке, располагая секундомером, и измеряя время t_k, за которое совершится k полных колебаний, можно найти период колебаний 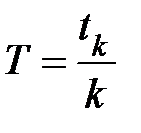конструкции из сплошных цилиндров.

Если использовать наручные часы, то погрешность отсчёта составит примерно 1 с. При достаточной в данном случае относительной погрешности определения периода на уровне 5% можно взять n = 20. Установка позволяет также осуществлять прямые измерения угловой амплитуды колебаний. Шкала позволяет отсчитывать угол с точностью примерно 1^о, т. е. радиан, так что для сохранения приемлемой точности не следует измерять угловые амплитуды, которые меньше 10^о. При такой относительной погрешности даже угол может считаться малым, ибо замена в выражении для потенциальной энергии выражение 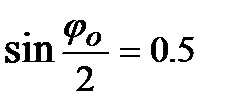на 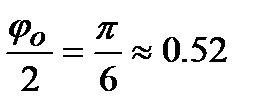даёт относительную погрешность на уровне 4%.

Краткая теория работы.

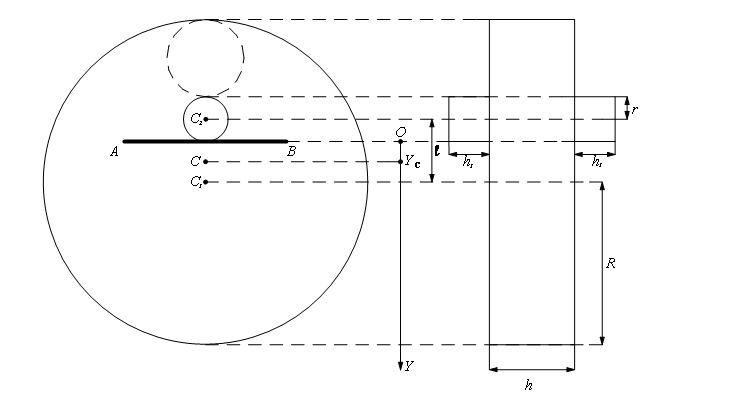
Рисунок 2

Рассмотрим конструкцию (см. рис. 2), состоящую из трёх сплошных цилиндров, показанную на рисунке (заштрихованный цилиндр – съёмный). Пусть ρ – плотность материала цилиндров. Тогда массы цилиндров и масса системы равны

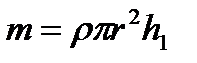, , . (1)

Если систему поставить на две горизонтальные направляющие АВ и отклонить от положения равновесия, в котором центр масс С системы занимает самое низкое положение, то предоставленная самой себе система начнёт совершать колебания. Координата y_сцентра масс системы (см. рисунок) определяется соотношением

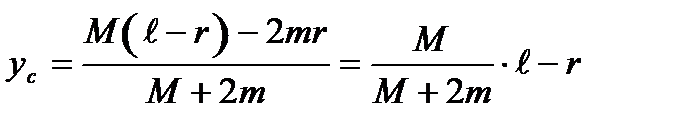(2)

Момент инерции системы относительно оси, проходящей через центр масс Снаходится по теореме Гюйгенса-Штейнера:

и (3)

Полная механическая энергия системы равна сумме кинетической и потенциальной энергий. Кинетическая энергия системы при качении по направляющим АВ находится по теореме Кёнига:

,

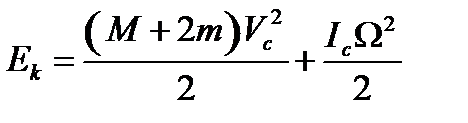где – угловая скорость вращения системы. Если качение происходит без проскальзывания, то скорость точки контакта системы с опорой равна нулю. Поэтому скорость центра масс связана с угловой скоростью соотношением 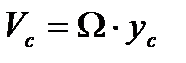. Таким образом,

(4)

Потенциальная энергия системы определяется высотой поднятия центра масс системы над положением равновесия. При повороте на угол φ центр масс системы поднимается на высоту . Считая угол отклонения малым, имеем 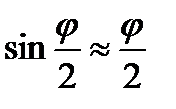и тогда, считая потенциальную энергию равной нулю в положении равновесия, получим для потенциальной энергии в отклонённом положении выражение:

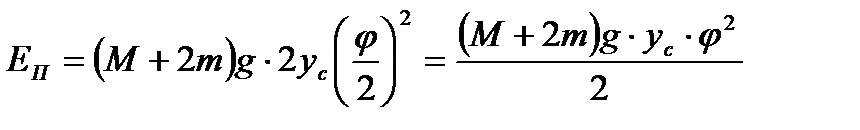(5)

Учитывая, что угловая скорость связана с углом отклонения соотношением 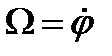, получим для полной механической энергии выражение:

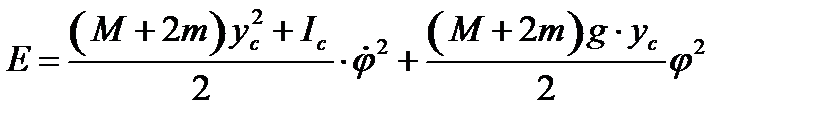(6)

Если пренебречь всеми силами трения, то полная механическая энергии системы сохраняется, т. е. энергия постоянна. Поэтому дифференцируя (6) по времени и отбрасывая тривиальное решение 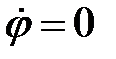, получим дифференциальное уравнение гармонических колебаний:

(7)

Циклическая частота ω и период T этих колебаний равны соответственно

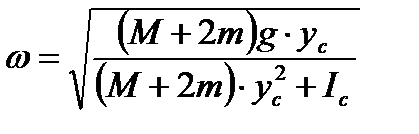, . (8)

Реально на рассматриваемую конструкцию при колебаниях действуют две диссипативные силы: сила вязкого трения о воздух и сила трения качения (см. рис. 3).

Влияние силы вязкого трения сказывается тем меньше, чем больше масса конструкции и меньше её угловая скорость , т. е. угловая амплитуда колебаний. Для данной установки, как показывают расчёты, влиянием силы вязкого трения можно пренебречь. Трение качения возникает вследствие того, что при качении деформации опоры и катящегося тела не вполне симметричны и упруги (на рисунке показана только деформация опоры в сильно преувеличенном виде). При этом сила нормальной реакции N = mg оказывается вынесенной вперёд относительно центра цилиндра Сна отрезок, длина которого S называется коэффициентомтре­ния качения. Смысл этого названия состоит в следующем. Сила трения (F_ТР), направленная против скорости , момент которой относительно оси, проходящей через центр масс,

Рисунок 3

практически равен F_ТР ∙r (деформа­ция цилиндра реально очень мала!), увеличивает угловую скорость вращения диска, но одновременно уменьшает скорость центра масс. Если, однако, что обычно подразумевается, проскальзывание при качении отсутствует, то , так что тормозит вращение диска именно сила реакции опоры (N), момент которой относительно оси, проходящей через центр масс, равен NS. Опыт показывает, что сила трения качения обычно очень мала, т. е. можно считать, что

F_ТРr ≈NS = mgS,

так что

В, принципе,для сохранения аналогии с силой сухого трения скольжения можно было бы величину 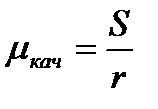называть коэффициентом трения качения, тогда ,однако как сказано выше, исторически сложилось так, что коэффициентом трения качения называется величина S.Поэтому при наличии трения качения вместо уравнения (7) мы имеем следующее уравнение

где знак соответствует движению центра масс направо (поворот системы по часовой стрелке) и знак «минус» соответствует повороту против часовой стрелки. Поскольку постоянная правая часть в дифференциальном уравнении не изменяет величину ω, то она по-прежнему выражается формулой (8). Колебания при этом, однако, затухают, и если обозначить 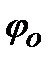начальный угол отклонения ( 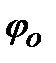> 0, т. е. система при t = 0 повёрнута против часовой стрелки), то спустя период Т отклонение составит

,

а спустя n периодов:

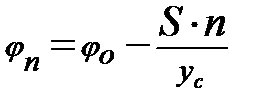(9)

Измеряя, таким образом, 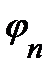,можно определить коэффициент трения качения S.Зависимость 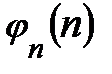линейная, поэтому лучшим способом определения S является метод наименьших квадратов, который в данном случае даёт

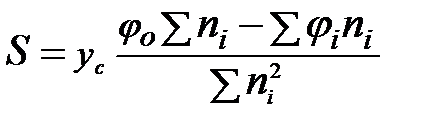(10)

При этом подразумевается, конечно, что угол измеряется в радианах (по шкале прибора он отсчитывается в градусах: рад)