Нечувствительность стеганосообщения к сжатию и формальные достаточные условия ее обеспечения
Любое преобразование информационной системы, в частности, стеганопреобразование (СП) контейнера, формально представимо в виде совокупности определенных возмущений СНЧ и СНВ соответствующих матриц. Разные элементы полного набора параметров реагируют по-разному на одно и тоже возмущающее воздействие.
Выясним, как и какие из полного набора формальных параметров, определяющих ЦИ, реагируют на сжатие, и выберем из них наименее чувствительные к этому виду возмущения. Очевидно, что если СП будет проводиться таким образом, что его формальным выражением будет возмущение именно этих параметров, то естественно ожидать, что при сжатии заполненного контейнера погруженная в него ДИ не пострадает (или пострадает незначительно), что и является основной идеей для получения последующих результатов.
Будем анализировать часть полного набора параметров – совокупность СНВ матриц, отвечающих ЦИ.
Пусть матрица изображения  имеет размеры
имеет размеры  . Предварительным шагом при организации сжатия является разбиение
. Предварительным шагом при организации сжатия является разбиение  на блоки. Обозначим
на блоки. Обозначим  - матрицу отдельного стандартного
- матрицу отдельного стандартного  блока. Для каждого блока возможно построение нормального сингулярного разложения:
блока. Для каждого блока возможно построение нормального сингулярного разложения:
 , (1)
, (1)
где 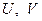 ― ортогональные матрицы размера
― ортогональные матрицы размера  , столбцы
, столбцы 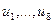 матрицы
матрицы  , называемые левыми СНВ, лексикографически положительны;
, называемые левыми СНВ, лексикографически положительны; 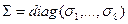 ,
, 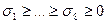 - СНЧ.
- СНЧ.
Результат СП, как и сжатия, формализуем в виде совокупностей возмущений СНЧ и СНВ множества блоков, но анализировать будем только возмущения СНВ. Выделим из СНВ 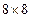 -блоков наименее чувствительные к сжатию, возмущения которых в результате СП обеспечат нечувствительность к сжатию получаемого СС (с учетом требования его надежности восприятия).
-блоков наименее чувствительные к сжатию, возмущения которых в результате СП обеспечат нечувствительность к сжатию получаемого СС (с учетом требования его надежности восприятия).
СНЧ  (как и любой другой матрицы) являются хорошо обусловленными:
(как и любой другой матрицы) являются хорошо обусловленными:
 ,
,
где 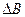 - матрица возмущающего воздействия (в частности, матрица возмущения блока
- матрица возмущающего воздействия (в частности, матрица возмущения блока  при сжатии). Наиболее ярко особенности возмущений при сжатии проявляются для наименьших СНЧ: их значения становятся сравнимы друг с другом и близки к нулю.
при сжатии). Наиболее ярко особенности возмущений при сжатии проявляются для наименьших СНЧ: их значения становятся сравнимы друг с другом и близки к нулю.
Чувствительность СНВ любой матрицы, в том числе и матрицы  блока ЦИ, различна, в отличие от чувствительности СНЧ, и в соответствии с соотношением
блока ЦИ, различна, в отличие от чувствительности СНЧ, и в соответствии с соотношением
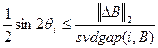 при условии
при условии 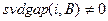 , (2)
, (2)
где  — угол между соответствующими исходным и возмущенным сингулярными векторами
— угол между соответствующими исходным и возмущенным сингулярными векторами  и
и  , мерой этой чувствительности является отделенность соответствующего сингулярному вектору СНЧ. Необходимо отметить, что
, мерой этой чувствительности является отделенность соответствующего сингулярному вектору СНЧ. Необходимо отметить, что 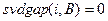 тогда и только тогда, когда
тогда и только тогда, когда  имеет кратные СНЧ, что для ЦИ, не подвергавшихся никакой обработке, не характерно.
имеет кратные СНЧ, что для ЦИ, не подвергавшихся никакой обработке, не характерно.
СНВ, которые отвечают СНЧ с малой отделенностью, являются настолько чувствительными к любым возмущающим воздействиям, что качественно их возмущения не содержат практически никакой информации о реальной величине этого воздействия. Из этого вытекает, что такие СНВ не имеет смысла задействовать при погружении ДИ: если процесс СП будет формализован совокупностью возмущений таких векторов, то полученное СС окажется чувствительным к любому возмущающему воздействию, в частности, к сжатию. Таким образом, погружение ДИ имеет смысл проводить так, чтобы формальным представлением процесса СП была совокупность возмущений СНВ блоков матрицы ОС, соответствующие СНЧ которых имеют значительные отделенности, приводящие к малой чувствительности векторов (следовательно, и СС) к любому возмущающему воздействию, а значит и к сжатию.
По известной теореме Фробениуса любая неразложимая неотрицательная матрица  всегда имеет положительное собственное значение
всегда имеет положительное собственное значение  , являющееся простым корнем характеристического уравнения. Модули всех других собственных значений не превосходят
, являющееся простым корнем характеристического уравнения. Модули всех других собственных значений не превосходят  . Собственному значению
. Собственному значению  соответствует собственный вектор
соответствует собственный вектор 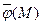 с положительными координатами.
с положительными координатами.
Для матрицы  блока контейнера с нормальным сингулярным разложением (1) матрица
блока контейнера с нормальным сингулярным разложением (1) матрица 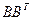 является симметричной неотрицательной матрицей, для которой имеет место соотношение:
является симметричной неотрицательной матрицей, для которой имеет место соотношение:
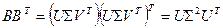 ,
,
которое в силу ортогональности матрицы  и лексикографической положительности ее столбцов, а также диагональности матрицы
и лексикографической положительности ее столбцов, а также диагональности матрицы  представляет собой нормальное спектральное разложение
представляет собой нормальное спектральное разложение 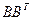 , определяемое однозначно, при этом собственные значения матрицы
, определяемое однозначно, при этом собственные значения матрицы 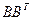 равны квадратам СНЧ
равны квадратам СНЧ  , в частности,
, в частности, 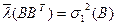 , а левые СНВ
, а левые СНВ  - ортонормированные лексикографически положительные собственные векторы
- ортонормированные лексикографически положительные собственные векторы 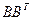 . По теореме Фробениуса собственному значению
. По теореме Фробениуса собственному значению  отвечает собственный вектор
отвечает собственный вектор  с положительными координатами, являющийся одновременно левым СНВ
с положительными координатами, являющийся одновременно левым СНВ 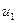 , отвечающим максимальному СНЧ
, отвечающим максимальному СНЧ 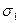 блока
блока  .
.
Аналогичное утверждение будет следовать для правого СНВ  блока, отвечающего
блока, отвечающего 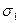 , поскольку для симметричной матрицы
, поскольку для симметричной матрицы 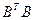 имеет место равенство:
имеет место равенство:
 .
.
Таким образом, в любой неразложимой неотрицательной матрице, какой и является  , левый и правый СНВ, отвечающие максимальному СНЧ, имеют положительные координаты. Необходимо отметить, что левый (правый) СНВ, все компоненты которого положительны, единственный для
, левый и правый СНВ, отвечающие максимальному СНЧ, имеют положительные координаты. Необходимо отметить, что левый (правый) СНВ, все компоненты которого положительны, единственный для  в силу ортонормированности СНВ. Важно, что независимо от возмущающего воздействия, которое претерпевает ЦИ, матрицы его блоков остаются неразложимыми неотрицательными, а значит и обсуждаемые СНВ должны после возмущения (даже сильного) иметь все положительные координаты, поэтому эти векторы является не только устойчивыми, но и sign-устойчивыми (sign-нечувствительніми) к любому возмущающему воздействию,
в силу ортонормированности СНВ. Важно, что независимо от возмущающего воздействия, которое претерпевает ЦИ, матрицы его блоков остаются неразложимыми неотрицательными, а значит и обсуждаемые СНВ должны после возмущения (даже сильного) иметь все положительные координаты, поэтому эти векторы является не только устойчивыми, но и sign-устойчивыми (sign-нечувствительніми) к любому возмущающему воздействию,
Ортонормированные СНВ  - матрицы
- матрицы 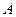 , являясь элементами пространства
, являясь элементами пространства  , лежат на
, лежат на 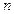 - мерной единичной сфере с центром в начале координат. Знаки координат каждого СНВ определяются координатным ортантом в
- мерной единичной сфере с центром в начале координат. Знаки координат каждого СНВ определяются координатным ортантом в 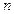 -мерном пространстве, содержащим этот СНВ. Классическое понятие нечувствительности определяется
-мерном пространстве, содержащим этот СНВ. Классическое понятие нечувствительности определяется 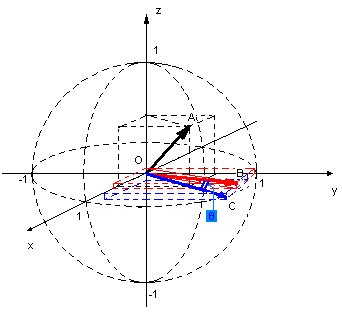 малым углом поворота СНВ от своего первоначального положения при малом возмущении исходных данных, при этом направление поворота никак не учитывается. Если поворот, пусть даже очень малый, выведет СНВ за границы первоначального координатного ортанта, это приведет к изменению знаков его элементов. Конечно, чем меньше угол отклонения, т.е. чем устойчивее вектор в классическом смысле, тем меньше вероятность выхода за границы исходного координатного ортанта. Однако возможны ситуации, когда даже малое возмущение
малым углом поворота СНВ от своего первоначального положения при малом возмущении исходных данных, при этом направление поворота никак не учитывается. Если поворот, пусть даже очень малый, выведет СНВ за границы первоначального координатного ортанта, это приведет к изменению знаков его элементов. Конечно, чем меньше угол отклонения, т.е. чем устойчивее вектор в классическом смысле, тем меньше вероятность выхода за границы исходного координатного ортанта. Однако возможны ситуации, когда даже малое возмущение
СНВ приведет его к переходу через координатную плоскость.
В случае n=3 геометрическая интерпретация сказанного представлена на рисунке. СНВ  находится в первом октанте, является нечувствительным к возмущающим воздействиям, все его координаты положительны, но при этом аппликата близка к нулю, вектор практически лежит в плоскости ХОУ. Это приводит к тому, что даже малый угол отклонения
находится в первом октанте, является нечувствительным к возмущающим воздействиям, все его координаты положительны, но при этом аппликата близка к нулю, вектор практически лежит в плоскости ХОУ. Это приводит к тому, что даже малый угол отклонения 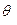 , внутренность которого пересекает ХОУ, выведет
, внутренность которого пересекает ХОУ, выведет  за пределы первого октанта (на рис. – вектор
за пределы первого октанта (на рис. – вектор 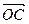 ), изменяя знак аппликаты. Для сравнения на рисунке представлен вектор
), изменяя знак аппликаты. Для сравнения на рисунке представлен вектор 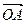 : даже если предположить, что он является чувствительным к возмущающим воздействиям, за пределы первого октанта его сможет вывести лишь сравнительно большой угол отклонения.
: даже если предположить, что он является чувствительным к возмущающим воздействиям, за пределы первого октанта его сможет вывести лишь сравнительно большой угол отклонения.
Определение. Вектор 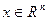 будем называть sign-чувствительным к возмущающим воздействиям (ВВ), если даже малые ВВ могут привести к изменению знаков координат вектора
будем называть sign-чувствительным к возмущающим воздействиям (ВВ), если даже малые ВВ могут привести к изменению знаков координат вектора 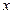 , и sign-нечувствительным в противном случае.
, и sign-нечувствительным в противном случае.
Очевидно, что вектор 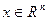 является sign-чувствительным, если составляет малый угол с координатной плоскостью (координатными плоскостями), о чем свидетельствует малость модулей его некоторых координат по сравнению с другими координатами. Однако, в отличие от классического понятия чувствительности, sign-чувствительный вектор может не отреагировать изменением знака координат даже на большой угол поворота (т.к. здесь важно направление этого поворота).
является sign-чувствительным, если составляет малый угол с координатной плоскостью (координатными плоскостями), о чем свидетельствует малость модулей его некоторых координат по сравнению с другими координатами. Однако, в отличие от классического понятия чувствительности, sign-чувствительный вектор может не отреагировать изменением знака координат даже на большой угол поворота (т.к. здесь важно направление этого поворота).
Из вышесказанного вытекает истинность следующей теоремы.
Теорема.Достаточным условием sign-нечувствительности нормированного вектора 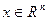 является сравнимость между собой значений модулей всех его координат (малый разброс значений модулей координат в сегменте [0,1]), что геометрически соответствует сравнимости углов между вектором и его проекциями на координатные плоскости. Достаточным условием sign-чувствительности нормированного вектора
является сравнимость между собой значений модулей всех его координат (малый разброс значений модулей координат в сегменте [0,1]), что геометрически соответствует сравнимости углов между вектором и его проекциями на координатные плоскости. Достаточным условием sign-чувствительности нормированного вектора 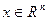 является наличие сравнительно малых по модулю координат (или достаточно большой разброс модулей координат в сегменте [0,1]).
является наличие сравнительно малых по модулю координат (или достаточно большой разброс модулей координат в сегменте [0,1]).
Заметим, что из классической нечувствительности вектора 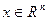 sign-нечувствительность, вообще говоря, не следует. Верно и обратное: из sign-нечувствительности вектора не следует его нечувствительность. Поэтому сделать какие-то выводы об одном виде нечувствительности по наличию или отсутствию другого вида, вообще говоря, нельзя.
sign-нечувствительность, вообще говоря, не следует. Верно и обратное: из sign-нечувствительности вектора не следует его нечувствительность. Поэтому сделать какие-то выводы об одном виде нечувствительности по наличию или отсутствию другого вида, вообще говоря, нельзя.
Свойство sign-устойчивости присуще левому и правому СНВ, отвечающим максимальному СНЧ, как до, та и после возмущающего воздействия, которое оставляет матрицу блока неразложимой неотрицательной. Очевидно, что это возможно лишь в том случае, когда обсуждаемые СНВ будут близки к n-оптимальному 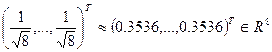 . Проведенный вычислительный эксперимент подтверждает полученное теоретическое заключение. Иллюстрацией этому являются левый, правый СНВ, отвечающие максимальному СНЧ одного случайно выбранного блока случайно выбранного ЦИ (табл.5). ЦИ брались различными для каждого примера табл.5.
. Проведенный вычислительный эксперимент подтверждает полученное теоретическое заключение. Иллюстрацией этому являются левый, правый СНВ, отвечающие максимальному СНЧ одного случайно выбранного блока случайно выбранного ЦИ (табл.5). ЦИ брались различными для каждого примера табл.5.
Таблица 5 –
Сингулярные векторы блоков матриц изображений, отвечающие максимальным сингулярным числам, при разном качестве сжатия
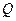 | Сингулярный вектор |
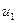 : 0.3898 0.4007 0.4079 0.3960 0.3679 0.3193 0.2678 0.2351 : 0.3898 0.4007 0.4079 0.3960 0.3679 0.3193 0.2678 0.2351 | |
 : 0.2370 0.1812 0.1695 0.2714 0.3965 0.4957 0.4691 0.4309 : 0.2370 0.1812 0.1695 0.2714 0.3965 0.4957 0.4691 0.4309 | |
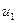 : 0.3107 0.3273 0.3497 0.3656 0.3701 0.3675 0.3659 0.3667 : 0.3107 0.3273 0.3497 0.3656 0.3701 0.3675 0.3659 0.3667 | |
 : 0.4020 0.3885 0.3673 0.3462 0.3318 0.3265 0.3273 0.3299 : 0.4020 0.3885 0.3673 0.3462 0.3318 0.3265 0.3273 0.3299 | |
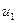 : 0.2438 0.2435 0.2574 0.3268 0.3926 0.4206 0.4375 0.4310 : 0.2438 0.2435 0.2574 0.3268 0.3926 0.4206 0.4375 0.4310 | |
 : 0.3482 0.3504 0.3539 0.3566 0.3570 0.3561 0.3537 0.3525 : 0.3482 0.3504 0.3539 0.3566 0.3570 0.3561 0.3537 0.3525 | |
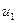 : 0.3542 0.3506 0.3499 0.3521 0.3534 0.3528 0.3556 0.3598 : 0.3542 0.3506 0.3499 0.3521 0.3534 0.3528 0.3556 0.3598 | |
 : 0.3485 0.3427 0.3544 0.3468 0.3570 0.3568 0.3599 0.3618 : 0.3485 0.3427 0.3544 0.3468 0.3570 0.3568 0.3599 0.3618 | |
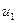 : 0.3416 0.3487 0.3585 0.3620 0.3562 0.3487 0.3528 0.3595 : 0.3416 0.3487 0.3585 0.3620 0.3562 0.3487 0.3528 0.3595 | |
 : 0.3409 0.3448 0.3452 0.3519 0.3484 0.3525 0.3708 0.3724 : 0.3409 0.3448 0.3452 0.3519 0.3484 0.3525 0.3708 0.3724 | |
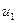 : 0.4059 0.3903 0.3917 0.3908 0.3880 0.3545 0.2663 0.1718 : 0.4059 0.3903 0.3917 0.3908 0.3880 0.3545 0.2663 0.1718 | |
 : 0.2991 0.2064 0.2047 0.3272 0.4022 0.4039 0.4614 0.4256 : 0.2991 0.2064 0.2047 0.3272 0.4022 0.4039 0.4614 0.4256 | |
| TIF-изображение | 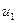 : 0.3527 0.3513 0.3512 0.3534 0.3535 0.3525 0.3558 0.3580 : 0.3527 0.3513 0.3512 0.3534 0.3535 0.3525 0.3558 0.3580 |
 : 0.3462 0.3462 0.3517 0.3505 0.3553 0.3587 0.3589 0.3606 : 0.3462 0.3462 0.3517 0.3505 0.3553 0.3587 0.3589 0.3606 |
Таким образом, при организации СП погружение ДИ должно происходить так, чтобы возмущение обсуждаемого (обсуждаемых) СНВ блоков в ходе СП оставляло его (их) близким к n-оптимальному.
Из всего вышесказанного вытекает, что достаточным условием обеспечения нечувствительности (малой чувствительности) СС к сжатию является такая организация процесса СП, формальным представлением которого является совокупность возмущений левых и/или правых СНВ блоков матрицы контейнера, полученных после ее стандартного разбиения, отвечающих (отвечающего) максимальным СНЧ ( 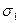 ) блоков.
) блоков.
Замечание 1. Возмущение СНВ, отвечающего максимальному СНЧ блока нельзя рассматривать обособленно от возмущений остальных СНВ, поскольку в силу ортормированности всех СНВ блока возмущение 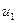 (
(  ) необходимо приведет к возмущению всех остальных, что увеличит величину
) необходимо приведет к возмущению всех остальных, что увеличит величину 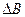 (и это уже произойдет безотносительно к процессу СП). Поэтому при организации процесса СП необходимо будет для конкретных разрабатываемых СА обеспечить приведение всех СНВ к ортонормированному виду так, чтобы за счет этого приведения величина
(и это уже произойдет безотносительно к процессу СП). Поэтому при организации процесса СП необходимо будет для конкретных разрабатываемых СА обеспечить приведение всех СНВ к ортонормированному виду так, чтобы за счет этого приведения величина 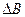 возросла незначительно.
возросла незначительно.
