Постановка задачи и метод решения.

Задача Дирихле для уравнения Лапласа с данными граничными условиями: найти функцию 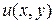, определенную на прямоугольнике 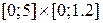, для которой выполнены следующие условия:

.

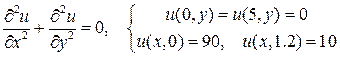Такая функция существует и единственна. В силу симметрии условий относительно прямой 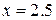(вертикальная ось симметрии прямоугольника), решение, в силу своей единственности, также должно быть симметрично: .

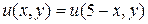Аппроксимационные данные:

· по оси абсцисс прямоугольник разбивается на 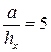интервалов

· по оси ординат прямоугольник разбивается на 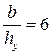интервалов

Разностная схема строится для чисел 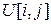, аппроксимирующих точное решение в точках с координатами , , .

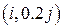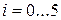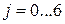Граничные условия:

.

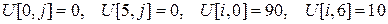То есть в точках границы прямоугольника все значения в узловых точках известны. Трехслойная схема «крест» во внутренних точках сетки выглядит следующим образом:

.

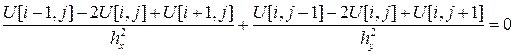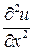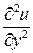Слагаемые аппроксимируют вторые производные и точного решения задачи в точке с координатами 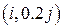. Таким образом, мы имеем дело с разностной схемой.

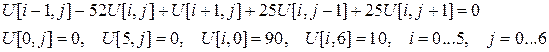
Рассмотрим уравнения схемы в точках 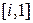как СЛУ относительно :

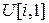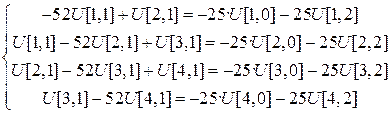
В силу упомянутой симметрии решения, для любого 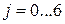выполняются равенства.

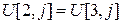и .

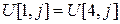Таким образом, данная СЛУ сводится к

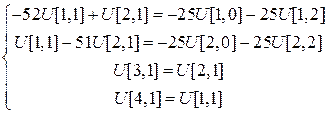
Решив эту систему относительно 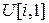,мы выразим величины 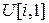через величины 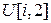линейно.

Теперь, для 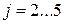, запишем соответствующие уравнения разностной схемы.

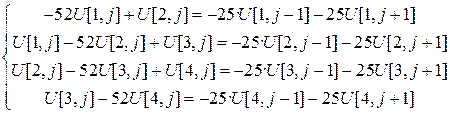
Согласно равенствам 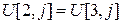и 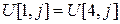, данная система принимает вид.

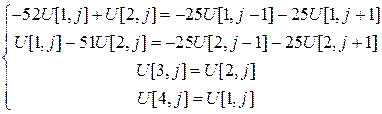
Перейдем к векторным обозначениям ( ):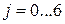

.

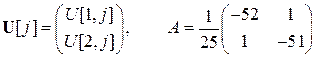В этих обозначениях полученные системы уравнений имеют вид.

.

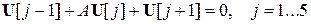При этом из граничных условий следует, что

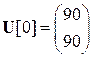и .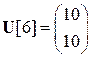

То есть мы имеем пять линейных векторных уравнений с пятью неизвестными векторами:

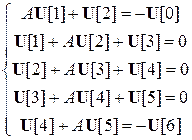
К подобным системам применим формализм метода прогонки.

Именно, предположим, что имеется последовательность матриц 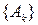и векторов 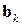( 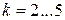), для которой выполнятся равенства.

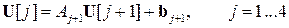
Подставляя данное равенство во второе, третье и четвертое уравнение системы, получим.

,

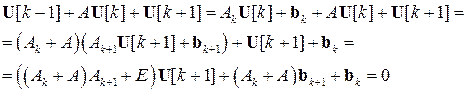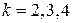
Как и в выводе формул метода прогонки, полагаем.

Откуда следует, что .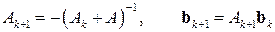

Подставляя равенство 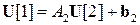в первое уравнение системы, получим 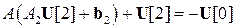. Откуда, как и в классическом методе прогонки, можно заключить, что 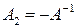и .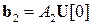

Итак, последовательности матриц 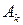и векторов 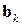( 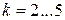) определены следующей рекурсией

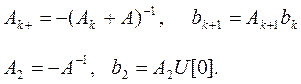
Эти последовательности легко вычисляются на ЭВМ.

Подставляя равенство 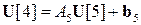в последнее уравнение системы, получим 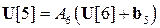. Таким образом, обратный ход прогонки задается формулами.

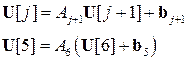
Таблица 2 - реализуя этот алгоритм на ЭВМ, мы получим следующий результат

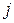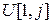		71.86	56.43	43.01	31.08	20.19
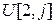		76.16	62.49	49.06	35.88	22.89

Таким образом, решение разностной схемы имеет вид.

Таблица 3- решение разностной схемы

	20.19	22.89	22.89	20.19
	31.08	35.88	35.88	31.08
	43.01	49.06	49.06	43.01
	56.43	62.49	62.49	56.43
	71.86	76.16	76.16	71.86

(началу координат отвечает левая нижняя клетка таблицы).

Листинг программы (матрицы 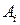обозначены как )

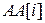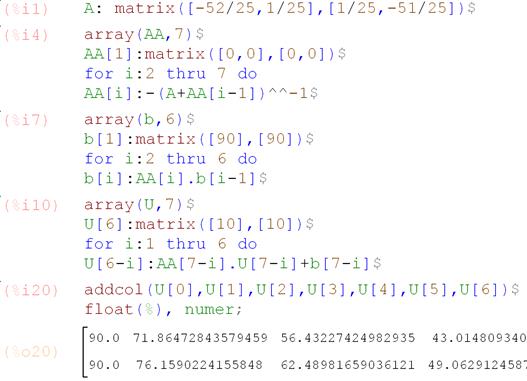
Вывод

Выполнено подробное решение задачи Коши аналитическим методом, а так же методом прогонки:

1. Постановка задачи и метод решения.

2. Аналитическое решение.

3. Результаты решения: массивы 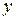и и величина .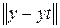

4. Листинг программы и окно результатов.

Выполнено подробное решение задачи Дирихле для уравнения Лапласа на прямоугольнике методом конечных разностей:

1. Постановка задачи и метод решения.

2. Исследование аппроксимации и устойчивости.

3. Листинг программы и окно результатов