Рычков С. П. MSC.Visual NASTRAN для Windows С.П. Рычков М: НТ-пресс 2004 г. 552 с

Содержание разделов дисциплины

Типовые задачи анализа, синтеза и оптимизации на этапе конструкторского проектирования РЭС. Организация математического и программного обеспечения для их решения.

Классификация задач математических моделей и методов топологического проектирования РЭС.

Математические модели конструкций РЭС, используемые в задачах топологического проектирования.

Методы и алгоритмы решения задачи компоновки.

Модели и алгоритмы размещения элементов РЭС на коммутационном поле.

Алгоритмы трассировки соединений в РЭС.

Основные задачи анализа и верификации конструкций РЭС. Математические модели процессов и полей различной физической природы в конструкциях РЭС. Оптимизация параметров и характеристик РЭС.

Методы, модели и алгоритмы решения задач учета статистического разброса параметров при проектировании РЭС.

Основные направления и тенденции развития и повышения эффективности современных САПР РЭС.

Конспект лекций по дисциплине

Лекция 1.

РАЗДЕЛ 1 /1, с. 5-30, 150-157/.. Введение. Цель и задачи дисциплины. Основные понятия и определения. Современное состояние автоматизированного проектирования РЭС. Состав и возможности современных САПР РЭС. Наиболее распространенные программные комплексы конструкторско-топологического и схемотехнического проектирования РЭС. CALS -технология. Техническая база современных САПР РЭС. Телекоммуникационные технологии и развитие автоматизированного проектирования. Экономические аспекты применения современных САПР РЭС.

Целью дисциплины является овладение теоретическими знаниями, практическими навыками и умениями решения задач проектирования РЭС с помощью методов и средств автоматизации проектных работ, использующих современные информационные технологии, методы математического моделирования и оптимизации. Основными задачами при освоении дисциплины являются изучение возможностей и особенностей применения и развития современных САПР РЭС, методов, математического обеспечения и процедур синтеза, анализа, оптимизации конструкций и технологических процессов производства РЭС, верификации и принятия проектных решений.

С точки зрения содержания решаемых задач процесс проектирования можно разбить на следующие этапы:

1. Системотехническое проектирование, при котором выбираются и формулируются цели проектирования, обосновываются исходные данные и определяются принципы построения систе­мы. При этом формируется структура проектируемого объек­та, его составных частей, которыми обычно являются функ­ционально завершенные блоки, определяются энергетические и информационные связи между составными частями. В резуль­тате формулируются частные технические задания на проек­тирование отдельных составных частей объекта.

2. Функциональное проектирование, применительно к РЭС называемое также схемотехническим, имеет целью аппаратурную реализацию составных частей системы (комплексов, устройств, узлов). При этом выбирают элементную базу, принципиаль­ные схемы и оптимизируют параметры (осуществляют структурный и параметрический синтез схем) с точки зрения обеспечения наилучшего функционирования и эффективного производства. При выборе элементной базы и синтезе схем стремятся учитывать конструкторско-технологические требования.

3. Конструирование, называемое также техническим проек­тированием, решает задачи компоновки и размещения элемен­тов и узлов, осуществления печатных и проводных соединений для РЭС всех уровней (модулей, ячеек, блоков, шкафов), а также задачи теплоотвода, электрической прочности, защиты от внешних воздействий и т.п. При этом стремятся оптимизи­ровать принимаемые решения по конструктивно-технологи­ческим, экономическим и эксплуатационным показателям.

На этом этапе проектирования разрабатывают техническую документацию, необходимую для изготовления и эксплуатации РЭС.

4. Технологическая подготовка производства обеспечивает разработку технологических процессов изготовления отдельных блоков и всей системы в целом. На этом этапе проектирова­ния создается технологическая документация на основе пред­шествующих результатов.

Каждый этап проектирования сво­дится к формированию описаний проектируемого РЭС, относя­щихся к различным иерархическим уровням и аспектам его создания и работы. Этапы проектирования состоят из отдельных проектных процедур, которые заканчиваются частным проектным реше­нием. Типичными для проектирования РЭС процедурами являются анализ и синтез описаний различных уровней и ас­пектов.

Процедура синтеза заключается в создании проектного ре­шения (описания) по заданным требованиям, свойствам и ог­раничениям. Например, широко используются при проектиро­вании РЭС процедуры синтеза электронных схем по их задан­ным характеристикам в частотной или временной области. При этом в процессе синтеза могут создаваться структура схемы (структурный синтез) либо определяться параметры элементов заданной схемы, обеспечивающие требуемые харак­теристики (параметрический синтез).

Процедура анализа состоит в определении свойств задан­ного (или выбранного) описания. Примерами такой процеду­ры могут служить расчет частотных или переходных характе­ристик электронных схем, определение реакции схемы на за­данное воздействие и др. Анализ позволяет оценить степень удовлетворения проектного решения заданным требованиям и его пригодность. Процедуры синтеза и анализа в процессе проектирования тесно связаны между собой, поскольку обе они направлены на создание приемлемого или оптимального проектного решения.

Типичной проектной процедурой является оптимизация, которая приводит к оптимальному (по определенному крите­рию) проектному решению. Например, широко используется оптимизация параметров электронных схем с целью наилуч­шего приближения частотных характеристик к заданным. Процедура оптимизации состоит в многократном анализе при целевом изменении параметров схемы до удовлетворительного приближения к заданным характеристикам. В сущности, оптимизация обеспечивает создание (синтез) проектного решения, но включает поэтапную оценку характеристик (анализ).

Проектные процедуры состоят из отдельных проектных операций. Например, в процессе анализа математических мо­делей РЭС приходится решать дифференциальные и алгебраи­ческие уравнения, осуществлять операции с матрицами и т.п. Такие операции могут иметь обособленный характер, но в це­лом они образуют единую проектную процедуру.

Проектные процедуры и операции выполняются в опреде­ленной последовательности, называемой маршрутом проекти­рования.

Маршруты проектирования могут начинаться с нижних ие­рархических уровней описаний (восходящее проектирование) либо с верхних (нисходящее проектирование).

САПР создаются в проектных, конструкторских, технологи­ческих организациях и на предприятиях с целью повышения качества, технико-экономической эффективности проектируе­мых и выпускаемых РЭС, уменьшения затрат на их создание и эксплуатацию, сокращения сроков и трудоемкости проекти­рования, а также повышения качества проектной документа­ции.

Системы автоматизированного проектирования состоят из совокупности средств методического, математического, лингвистического, программного, технического, информационного и организационного обеспечений.

Методическое обеспечение (МО) САПР включает в себя теорию процессов, происходящих в схемах и конструкциях РЭС, методы анализа и синтеза схем и конструкций радиоэлект­ронных устройств, систем и их составных частей, их математи­ческие модели, математические методы и алгоритмы численно­го решения систем уравнений, описывающих схемы и констру­кции РЭС. Указанные компоненты МО составляют ядро САПР. В методическое обеспечение САПР входят также алго­ритмические специальные языки программирования, термино­логия, нормативы, стандарты и другие данные. Очевидно, что разработка методического обеспечения САПР РЭС требует глубоких специальных знаний в областях радиотехники, эле­ктроники, в частности системотехники, схемотехники и микроэлект­роники, конструирования и технологии производства РЭС. От­сюда вытекает, что разработка методического обеспечения САПР РЭС — прерогатива специалистов в области радиотех­ники и электроники.

Обычно в качестве обособленных блоков в методическом обеспечении выделяются математическое и лингвистическое обеспечения.

Математическое обеспечение — это совокупность матема­тических моделей, методов и алгоритмов для решения задач автоматизированного проектирования.

Лингвистическое обеспечение представляет собой сово­купность языков, используемых в САПР для представления ин­формации о проектируемых объектах, процессе и средствах проектирования и для осуществления диалога между проекти­ровщиками и ЭВМ.

Если математическое и лингвистическое обеспечения яв­ляются полностью самостоятельными в составе САПР, под ме­тодическим обеспечением понимается совокупность докумен­тов, описывающих состав, правила отбора и эксплуатации средств автоматизированного проектирования.

Компоненты МО создаются на основе перспективных мето­дов проектирования, поиска новых принципов действия и тех­нических решений, эффективных математических и других мо­делей проектируемых объектов, применения методов многова­риантного проектирования и оптимизации, использования типовых и стандартных проектных процедур, стандартных вы­числительных методов.

Программное обеспечение (ПО) включает в себя документы с текстами программ, программы на машинных носителях (магнитных лентах, дисках и др.) и эксплуатационные докумен­ты, обеспечивающие функционирование САПР.

Программное обеспечение подразделяется на общесистем­ное и прикладное. Компонентами общесистемного ПО являют­ся, например, операционные системы, трансляторы с алгоритмических языков, супервизоры и т.п., то есть совокупность программ, которая осуществляет управление вводом и обрабо­ткой информации в ЭВМ, диалоговый режим работы и другие обслуживающие функции независимо от объекта проектирования. Прикладное ПО включает программы и пакеты прикладных программ, предназначенные непосредственно для получе­ния проектных решений. Прикладное ПО разрабатывается обычно совместно специалистами в области проектируемых РЭС и системного программирования.

Техническое обеспечение (ТО) САПР включает в себя устройства вычислительной и организационной техники, средства передачи данных, измерительные и другие устройства или их сочетания.

Информационное обеспечение (ИО) САПР состоит из описа­ния стандартных проектных процедур, типовых проектных ре­шений, типовых элементов РЭС, комплектующих изделий и их моделей, материалов, числовых значений параметров и других данных. Эти данные в закодированной форме записываются на машинных носителях: магнитных лентах и магнитных дисках. Основное назначение информационного обеспечения САПР— это уменьшение объемов информации, требуемой в процессе проектирования от разработчика РЭС, и исключение дубли­рования данных в прикладном ПО и ТО САПР.

Данные ПО обычно группируются в отдельные массивы, каждый из которых относится к определенному объекту описа­ния. Такие массивы называются файлами. Вся совокупность файлов образует базу данных, которую можно многократно использовать при проектировании различных РЭС для различ­ных этапов и уровней. Для создания, расширения, корректи­ровки и коллективного использования данных создаются спе­циальные системы управления базами данных (СУБД). Сово­купность баз данных, систем управления ими, а также относящихся к ним программных, языковых, технических и ор­ганизационных средств называется банком данных.

Организационное обеспечение САПР включает методичес­кие и руководящие материалы, положения, приказы, инструк­ции, штатные расписания, квалификационные требования и другие документы, обеспечивающие необходимую деятельность и взаимодействие различных подразделений организации и от­дельных пользователей при создании, эксплуатации и разви­тии САПР.

Основными структурными звеньями САПР являются подси­стемы. Подсистемой называется выделенная по некоторым признакам часть САПР, обеспечивающая получение закончен­ных проектных решений и соответствующих проектных доку­ментов. Различают объектно-ориентированные (объектные) и объектно-независимые (инвариантные) подсистемы.

Объектные подсистемы осуществляют непосредственное проектирование. Применительно к САПР, осуществляющим комп­лексное проектирование РЭС, объектными являются, например, подсистемы схемотехнического и конструкторского проектирова­ния. Для конструкторских САПР объектными являются подсис­темы компоновки, размещения, трассировки и т.п.

Инвариантные подсистемы выполняют функции управле­ния и обработки информации, не зависящие от объекта проек­тирования. Таковыми являются, например, подсистемы управ­ления САПР, диалоговых процедур, оптимизации, подсистемы ввода, обработки и вывода графической информации, подсис­темы информационно-поисковых процедур и др.

РАЗДЕЛ 2 /1, с. 34-64, 72-92/. Типовые задачи анализа, синтеза и оптимизации на этапе конструкторского проектирования РЭС. Организация математического обеспечения для их решения. Топологическое проектирование РЭС (компоновка, размещение, трассировка) как задача синтеза и структурной оптимизации. Задачи моделирования основных физических процессов и полей в РЭС как задачи анализа. Обеспечение характеристик РЭС как задача параметрической оптимизации.

Математическое описание проектируемого объекта назы­вают математической моделью. Математическая модель - это совокупность математических элементов (чисел, переменных, векторов, множеств и т.п.) и отношений между ними, которые с требуемой для проектирования точностью описывают свойст­ва проектируемого объекта. На каждом этапе проектирования используется свое математическое описание проектируемого объекта, сложность которого должна быть согласована с воз­можностями анализа на ЭВМ, что приводит к необходимости иметь для одного объекта несколько моделей различного уров­ня сложности.

В общей теории математического моделирования математи­ческую модель любого объекта характеризуют внутренними, внешними, выходными параметрами и фазовыми переменны­ми. Внутренние параметры модели определяются характерис­тиками компонентов, входящих в проектируемый объект, на­пример номиналы элементов принципиальной схемы. Если проектируемый объект содержит n элементарных компонентов, то и его математическая модель будет определяться парамет­рами 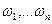, которые образуют вектор внутренних параметров 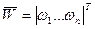. Каждый из параметров 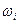в свою очередь, может быть функцией, вектором или еще более сложным ма­тематическим функционалом в зависимости от объекта проек­тирования.

Выходные параметры модели - это показатели, характери­зующие функциональные, эксплуатационные, конструкторско-технологические, экономические и другие характеристики проекти­руемого объекта. К таким показателям могут относиться коэффициенты передачи, масса и габариты проектируемого объекта, надежность, стоимость и т.п. Понятия внутренних и выходных параметров инвариантны, при моделировании на более сложном уровне выходные параметры могут стать внутр­енними и наоборот. Например, сопротивление резистора яв­ляется внутренним параметром при моделировании усилительного устройства, компонентом которого он является, но это сопротивление будет выходным параметром при моделировании самого резистора, что требуется при пленочном его исполнении. Вектор выходных параметров модели будем обозначать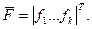

Внешние параметры модели - это характеристики внешней по отношению к проектируемому объекту среды, а также рабочие управляющие воздействия. Вектор внешних параметров в общем случае содержит множество самых различных соста­вляющих, к его составляющим с полным правом можно отнести все, что говорилось ранее о составляющих вектора внутренних параметров. Будем обозначать его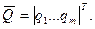

Уравнения математической модели могут связывать некоторые физические характеристики компонентов, которые полнос­тью характеризуют состояние объекта, но не являются выходными или внутренними параметрами модели (например, токи и напряжения в радиоэлектронных устройствах, внутренними параметрами которых являются номиналы элементов электри­ческих схем, а выходными параметрами - выходная мощность, коэффициент передачи и т.п.). Такие характеристики называют фазовыми переменными. Минимальный по размерности вектор фазовых переменных 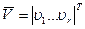, полностью характеризующий работу объекта проектирования, называют базисным вектором. Например, при составлении уравнений математической модели радиоэлектронных устройств в качестве базисного вектора 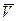можно использовать вектор узловых потенциа­лов либо вектор напряжений на конденсаторах и токов в индуктивностях - переменные состояния. Использование вектора фазовых переменных позволяет упростить алгоритмическую реализацию программ, составляющих уравнения математической модели устройства.

РАЗДЕЛ 3 /1, с. 31-34/. Классификация задач, математических моделей и методов топологического проектирования РЭС.

Задачи компоновки, размещения и трассировки. Основные типы алгоритмов их решения. Коммутационная схема. Применение теории графов и множеств при проектировании топологии.

Задача компоновки заключается в распределении модулей низшего уровня по конструктивным модулям высшего уровня. При этом считается, что каждый модуль является конструк­тивно неделимым компонентом по отношению к модулю более высокого уровня и, как правило, функционально и конструктивно унифицированным. Среди задач компоновки можно выделить два характерных класса. К первому из них относятся задачи, в которых осуществляется разбиение схемы устройств на конструктивные модули с учетом таких ограничений, как количество компонентов в модуле, число внешних выводов на модуле, суммарная площадь, занимаемая компонентами и соединениями, и т.п. Главными критериями оптимальности компоновки в этом случае являются минимум числа образующихся в результате компоновки модулей высшего уровня, минимум числа межсоединений между модулями и др. К от­меченным выше критериям и ограничениям могут быть до­бавлены и другие, например условия электромагнитной совмес­тимости в модуле, нормального теплообмена, минимизации задержек в распространении сигналов. Эти условия должны быть выяснены до начала компоновки либо проверяются по окончании компоновки.

Такие задачи возникают при разбиении схемы устройства на узлы большой степени сложности, к которым не предъявле­ны строгие требования в отношении их схемной и функциона­льной унификации. Примером таких задач являются задачи разбиения схемы на большие интегральные схемы частного применения, распределения микросхем по печатным платам, отдельных печатных плат по панелям и т. п. Подводя итог вы­шесказанному, отметим, что к первому классу задач компо­новки относятся такие, в которых критерии оптимизации и ог­раничения могут быть сведены к определенным конструктив­ным параметрам расположения отдельных компонентов в мо­дуле и их межсоединений.

Ко второму классу задач компоновки относятся задачи, в которых помимо конструктивных характеристик модулей суще­ственны и их функциональные характеристики. Эти задачи возникают, например, на этапе перехода от функциональных схем цифровых устройств к принципиальным электрическим схемам и состоят в выборе элементов логической схемы для типовых модулей (микросхем) из заданного конструктивного набора. Каждый из типовых модулей может включать неско­лько логических элементов или их функциональных групп, в общем случае соединенных между собой. Иногда эти задачи выделяют в отдельный класс и называют задачами покрытия функциональной схемы заданным набором конструктивных модулей. Эти задачи более трудны в формализации, их реше­ние до настоящего времени представляет значительные труд­ности.

Задачи размещения и трассировки являются тесно связан­ными, так как в процессе размещения определяются условия для трассировки межсоединений. Совместное решение этих за­дач представляет значительные трудности, и при алгоритми­ческом подходе к их решению эти задачи рассматриваются, как правило, раздельно. Сначала осуществляется размещение модулей низшего уровня в модуле высшего, например микро­схем на печатной плате, а затем осуществляется трассировка межсоединений. Если трассировка оказывается неудовлетвори­тельной, то процесс размещения повторяется с учетом недос­татков предыдущего варианта размещения.

Лекция 2.

РАЗДЕЛ 4 /1, с. 41-49/. Математические модели конструкций РЭС, используемые в задачах топологического проектированиям. Представление коммутационных схем в виде графа, мультиграфа и гиперграфа. Матричное представление графов. Графовые и матричные модели монтажно-коммутационного пространства.

В большинстве случаев для решения задач конструкторско­го проектирования радиоустройство представляется множест­вом конструктивных модулей, функциональное назначение ко­торых не конкретизируется и группы контактов которых свя­заны эквипотенциальными электрическими соединениями. Такое представление устройства называют коммутационной схемой.

В общем виде задачу размещения модулей низшего уровня в модуле высшего можно описать следующим образом: задана коммутационная схема устройства, требуется разместить мо­дули в некотором коммутационном пространстве таким обра­зом, чтобы обеспечить оптимальное значение некоторого функ­ционала.

Коммутационным пространством конструктивного модуля какого-либо уровня называют область, ограниченную габари­тами этого модуля, в которой располагаются модули предыду­щего уровня и осуществляются электрические соединения кон­тактов модулей низшего уровня. Различают регулярные и не­регулярные коммутационные пространства. Регулярные прост­ранства характеризуются конечным числом позиций для раз­мещения модулей низшего уровня и числом слоев, в которых располагаются трассы соединительных проводников. В нерегу­лярных пространствах нельзя заранее указать координаты по­зиций и число слоев проводников, так как размещаемые моду­ли имеют различные размеры и форму.

Вариантами регулярного коммутационного пространства могут быть панель с межсоединениями, печатная плата. Ти­пичными нерегулярными пространствами являются подложка; микросборки, кристалл интегральной схемы. Критерием оптимальности размещения в большинстве случаев является критерий минимума суммарной длины соединений, который интегральным образом учитывает многочисленные требования к расположению модулей и трасс их межсоединений, так как уменьшение длин соединений улучшает электрические характеристики устройства, упрощает трассировку межсоединений и трудоемкость изготовления платы, кроме того, данный кри­терий прост с точки зрения формализации.

Для измерения длин межсоединений с коммутационным пространством связывают некоторую систему координат (для плоского коммутационного пространства XOY). Расстояние между соединяемыми контактами модулей с координатами x_i, x_j и y_i, y_j соответственно можно определить одним из следующих способов:

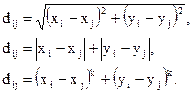
Первый способ соответствует прокладке проводных соедине­ний по кратчайшему расстоянию между соединяемыми контак­тами модулей — эвклидова метрика (рис. 3.2, а).Второй способ предполагает проведение трасс межсоединений по направле­ниям, параллельным координатным осям (сторонам пла­ты),— ортогональная метрика (рис. 1, б). Третий способ при­меняется, когда одновременно необходимо минимизировать сум­марную длину межсоединений и их максимальную длину. Действительно, при использовании этой формулы длинные сое­динения будут давать максимальный вклад в суммарную длину и критерий минимума суммарной длины межсоединений косвен­ным образом будет минимизировать и максимальные из них.

Результатом решения задач размещения является опреде­ление точного расположения на коммутационном пространстве центров модулей и координат их контактов, что совместно с принципиальной электрической схемой является основой для решения задачи трассировки.

а) б)

Рис. 1. Виды монтажных соединений.

Задачи трассировки можно разделить на две группы: трассировка проводного монтажа и трассировка печатных соединений. Трассировка проводных соединений относительно более проста, так как отдельные соединения электрически изолированы друг от друга. Поэтому в большинстве случаев она может быть сведена к задаче минимизации длины отдельных электрических цепей, если не возникает задача совместной оптимизации соединений монтажных схем, например, для обеспечения электромагнитной совместимости.

Задача трассировки печатного монтажа представляется го­раздо более сложной и решается в несколько этапов, которые включают определение требуемого числа слоев печати (рас­слоение монтажа), определение порядка трассировки каждого слоя печати, при котором обеспечи­вается отсутствие пересечений и ми­нимальная длина проводников, и соб­ственно трассировку соединений. Точная математическая формулиров­ка этих задач зависит от применяе­мой технологии изготовления печат­ного модуля, используемых методов трассировки проводников.

Постановка и решение перечисленных конструкторских за­дач на ЭВМ невозможны без определения математических мо­делей коммутационного пространства и принципиальной элек­трической схемы проектируемого устройства. Модели схем и коммутационного пространства, используемые для решения задач автоматизации конструкторского проектирования, мож­но условно разделить на несколько видов: модели, использую­щие аппарат теории симметрических графов; модели, исполь­зующие аппарат теории гиперграфов и ультраграфов; модели, использующие аппарат теории множеств; эвристические моде­ли.

Монтажно-коммутационное пространство (МКП) предназначено для размещения конструктивных модулей и трассировки соединений между их контактами, которые должны быть соединены электрическими цепями. Форма и, естественно, ма­тематическая модель МКП зависят от уровня модуля, для которого в данный момент решаются задачи конструирования (базовый матричный кристалл, печатная плата, панель и т.д.). В дальнейшем ограничимся только плоским монтажно-коммутационным пространством, соответствующим конструктивному модулю типа печатной платы. Без потери общности будем считать, что пространство имеет прямоугольную форму, так как введением областей, в которых запрещается размещение конструктивных модулей более низкого уровня или трассировки соединений, можно придать пространству произвольную форму. Так как МКП служит для решения двух задач — раз­мещения модулей и трассировки, то модели МКП, используе­мые для решения каждой задачи, будут иметь отличия.

Наибольшее распространение для решения задач размеще­ния конструктивных модулей в плоском МКП получили эврис­тические дискретные модели. Такие модели (будем их называть МКП1) строятся следующим образом (рис. 2, а): МКП раз­бивается на элементарные площадки (дискреты), каждая из которых предназначена для размещения одного конструктивного модуля более низкого уровня, например микросхемы на пе­чатной плате. Эти площадки в дальнейшем будем называть ди­скретами рабочего поля (ДРП). Каждый дискрет в процессе решения задачи размещения может находиться в одном из следующих состояний: свободен для размещения, занят, имеет определенный вес, запрещающий размещение в нем модуля, и т.д. Такая модель МКП отличается простотой и удобством для использования в эвристических алгоритмах размещения, однако она не является полностью формализованной [8,9].

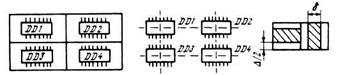а) б) в)

Рис. 2. Дискретные модели МКП.

Одной из разновидностей модели МКП 1 является модель с ортогональной сеткой, в узлах которой могут размещаться модули низкого уровня (рис. 3.4, б). Шаг сетки выбирается из условия возможности размещения модулей в соседних узлах сетки.

При размещении разногабаритных компонентов часто размер ДРП выбирают равным наибольшему общему делителю линейных размеров размещаемых модулей либо линейным размерам установочного места для наименьшего из модулей, если размеры всех модулей кратны. Заметим, что выбор шага дискретизации представляется весьма важным, так как при малых размерах ДРП увеличивается время решения задачи, зато повышается плотность заполнения МКП модулями низшего уровня.

Аналогичные дискретные модели используются и для решения задач трассировки. В этом случае дискрет является квадратом со сторонами, равными ширине проводника плюс зазор между ними (рис. 24, в). При этом считается, что проводник из каждого дискрета может быть проведен только в соседний ДРП.

Наибольшее распространение для решения задач разме­щения получили модели МКП в виде взвешенного графа VG(S, V), которые будем обозначать МКП2. Взвешенный граф VG представляет собой симметрический граф, в котором мно­жество вершин S соответствует множеству установочных позиций в коммутационном пространстве для модулей низ­шего уровня, а множество ветвей интерпретирует множество связей между соответствующими установочными позициями. Каждой ветви графа υ_ij присваивается вес p_ij, который равен числу условных единиц расстояния между центрами устано­вочных позиций s_i и s_j, интерпретируемых вершинами, инци­дентными данной ветви. Вес ветви p_ij определяется в зави­симости от метрики пространства по одной из формул.

Для описания взвешенного графа VG удобно использовать матрицу смежностей Q, строки и столбцы которой соответст­вуют вершинам графа, т.е. множеству установочных позиций в МКП, а элементы q_ij равны весу ветви, инцидентной i-й и j-й вершинам графа. Элементы, лежащие на главной диагонали матрицы смежностей Q, прини­маются равными нулю. Так, для МКП, показанного на рис. 3.5, а, модель в виде взвешен­ного графа при ортогональной метрике пространства приведена на рис. 3, б, а матрица смежностей Q имеет вид

		s1	s2	s3	s4
	s1
Q=	s2
	s3
	s4

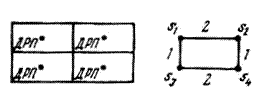а) б)

Рис. 3. Графовые модели МКП для решения задачи размещения

Для решения задач размещения применяются и другие графовые модели.

Большими возможностями для формализации процесса трассировки обладают комбинированные дискретно-графовые модели МКП3. В этом случае МКП моделируется симметрическим графом G(S, V), в котором каждому ДРП ставится в соответствие вершина графа. Вершины s_i и s_j соединяются ветвью, если они соответствуют соседним дискретам, через которые может проходить проводник. Трассы проводников могут проходить только по ветвям графа, а длина трасс определяется в соответствии с выбранной метрикой пространства. На рис. 4, а показаны модели МКП2 для трассировки

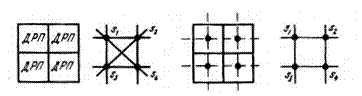по ортогональным направлениям и при допущении трассировки под углом в 45° (трассировка по шести направлениям).

а) б)

Рис. 4. Графовые модели МКП для решения задачи трассировки.

Симметрический граф G(S, V) с множеством вершин S и множеством ветвей V может быть описан в ЭВМ матрицей инциденций А, элемент которой a_ij = 1, если вершина s_i инцидентна ветви υ_ij,и a_ij = 0 в противном случае. Для графа, показанного на рис. 3.6, а, при допущении трассировки по восьми направлениям матрица инциденций имеет вид

Модель МКП3 очень широко распространена и позволяет при трассировке получить все множество кратчайших путей в отличие от МКП1, в которой обычно получают лишь один из возможных путей из этого множества. Кроме того, вводя вес для вершин и ветвей графа, можно регулировать скорость распространения числовой волны по определенным направле­ниям в волновых алгоритмах трассировки за счет введения соответствующих задержек.

Аналогична МКП3 и графовая модель пространства МКП4, также используемая для решения задач трассировки. Модель МКП4 представляет симметрический граф G(S,V),вершины которого s_i соответствуют узлам координатной сетки, нанесенной на плоское МКП, а ветви графа υ_ij— элементар­ным отрезкам координатной сетки, соединяющим две соседние точки (рис. 3.6, б). Особенностью модели МКП4 по сравне­нию с МКП3 является интерпретация ветви графа G(S, V)как элементарного отрезка проводника, который может быть проложен в этом месте МКП. По своим возможностям модель МКП4 эквивалентна МКП3.

Для моделирования коммутационного пространства при решении задач трассировки можно использовать модели в виде мультиграфа, т. е. симметрического графа, у которого существует хотя бы одна пара вершин, соединенных несколь­кими ветвями. Ветви, соединяющие одну и ту же пару вер­шин, называют кратными, а их максимальное число— мультичислом графа.

Одна из таких моделей МКП5 представляет мультиграф MG(S, V),в котором множество вершин графа S соответст­вует множеству установочных позиций в коммутационном про­странстве для модулей низшего уровня, а множество ветвей V — множеству взаимно независимых непосредственных пере­ходов между установочными позициями, т.е. множеству облас­тей, допускающих трассировку соединений между этими пози­циями без пересечений.

Мультиграф MG(S, V)может быть описан с помощью матрицы смежности Q, в которой, как и для взвешенного графа, элементы q_ij, лежащие на главной диагонали, при­нимаются равными нулю, а внедиагональные элементы а_и равны числу кратных ветвей, инцидентных i-й и j-й вершинам графа. Для примера на рис. 5, апоказаны фрагмент коммутационного пространства с установочными позициями и его модель в виде мультиграфа при допущении трассировки без пересечений трех проводников между соседними пози­циями.

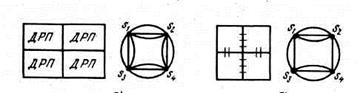а) б)

Рис. 5. Модели КПМ в виде мультиграфа

Матрица смежностей такого мультиграфа имеет вид