Линейные дифференциальные уравнения произвольного порядка
4.1 Линейное однородное дифференциальное уравнение
§ Линейное однородное дифференциальное уравнение имеет вид
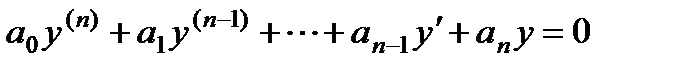 ,
,
где коэффициенты аk являются непрерывными функциями от х (в частности они могут быть постоянными или нулями). Полагая коэффициент а0(х) не равным нулю в некотором интервале 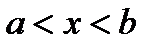 , мы можем разделить уравнение на него и получим
, мы можем разделить уравнение на него и получим
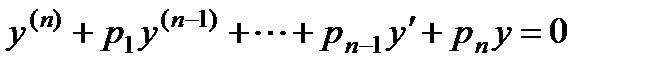 . (1)
. (1)
В дальнейшем говоря о линейном однородном уравнении мы будем подразумевать, что оно приведено к виду (1) с коэффициентом при старшей производной равным единице.
§ Для уравнения (1) справедливы следующие теоремы:
Т е о р е м а 1. Если у1 и у2 суть два (частных) решения уравнения (1), то у1 + у2
есть также решение этого уравнения.
Т е о р е м а 2. Если у1 есть решение уравнения (1), то С у1 есть также решение этого уравнения (С – любая постоянная).
Следствие. Если у1, у2,…,уп суть частные решения линейного однородного уравнения п – гопорядка, то выражение 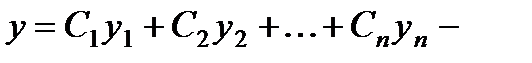 есть решение.
есть решение.
§ Вопрос о том, каким условиям должны удовлетворять частные решения, чтобы это
выражение являлось общим решением однородного уравнения, разрешается в связи с понятием линейной зависимости функций. Функции 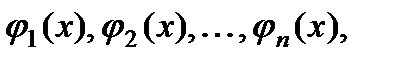 определенные в интервале (а,b) , называются линейно зависимыми в этом интервале, если существуют постоянные
определенные в интервале (а,b) , называются линейно зависимыми в этом интервале, если существуют постоянные 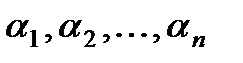 , не все равные нулю, такие, что для всех значений х в рассматриваемом интервале выполняется тождественно соотношение:
, не все равные нулю, такие, что для всех значений х в рассматриваемом интервале выполняется тождественно соотношение:
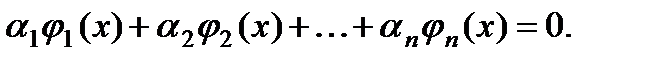
Если не существует таких постоянных 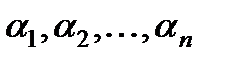 , чтобы это равенство имело место для всех рассматриваемых значений х (причем предполагается, что не все
, чтобы это равенство имело место для всех рассматриваемых значений х (причем предполагается, что не все 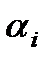 равны нулю), то функции называются линейно независимыми (в данном интервале). В последующем мы часто будем иметь дело с интервалом
равны нулю), то функции называются линейно независимыми (в данном интервале). В последующем мы часто будем иметь дело с интервалом 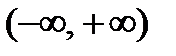 .
.
§ Пусть мы имеем п функций от х, имеющих непрерывные производные до
(п – 1)-го порядка:
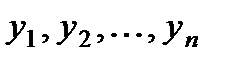 .
.
Определитель
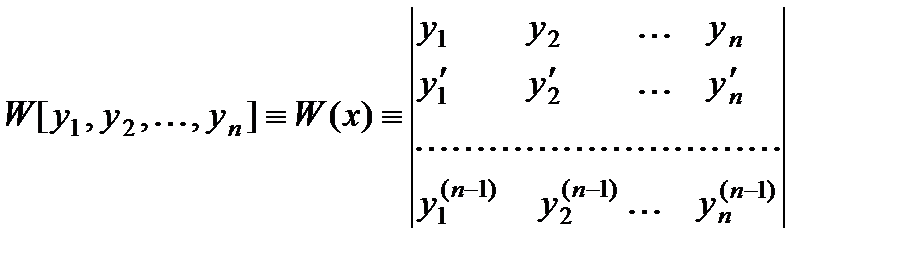
называется определителем Вронского этих функций.
Т е о р е м а 3. Если функции у1 , у2 , … , уп линейно зависимы, то определитель
Вронского тождественно равен нулю.
Т е о р е м а 4. Если решения у1 , у2 , … , уп линейно независимы [в интервале
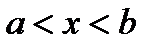 ], то
], то 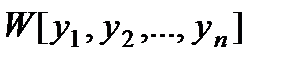 не обращается в нуль ни в одной точке рассматриваемого интервала.
не обращается в нуль ни в одной точке рассматриваемого интервала.
Теоремы 3 и 4 можно объединить в следующей формулировке: определитель
Вронского, составленный для системы п решений линейного уравнения п-го порядка (1), или тождественно равен нулю, или не обращается в нуль ни в одной точке того интервала, где коэффициенты уравнения непрерывны.
Любая система из п линейно независимых частных решений линейного однород-
ного уравнения (1) называется фундаментальной системой.
Т е о р е м а 5. Для всякого линейного однородного дифференциального уравнения
существует фундаментальная система.
Т е о р е м а 6. Если у1 , у2 , … , уп образуют фундаментальную систему решений
уравнения 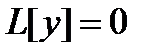 , то общее решение дается формулой:
, то общее решение дается формулой:
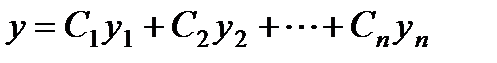 .
.
П р и м е р 13. Уравнение 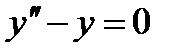 имеет, как легко проверить, два частных решения:
имеет, как легко проверить, два частных решения: 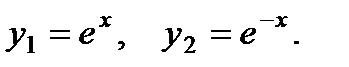 Для выяснения вопроса об их линейной зависимости или независимости составляем определитель Вронского:
Для выяснения вопроса об их линейной зависимости или независимости составляем определитель Вронского:
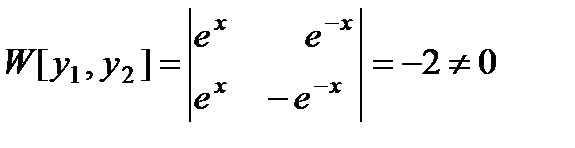 .
.
Следовательно, 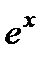 и
и 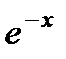 составляют фундаментальную систему, и общее решение напишется так:
составляют фундаментальную систему, и общее решение напишется так: 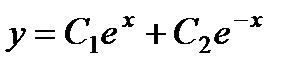 .
.
Т е о р е м а 7. Если мы имеем п + 1 частных решений уравнения (1)
у1 , у2 , … , уп+1,
то между ними необходимо существует линейная зависимость.
Т е о р е м а 8. Фундаментальная система вполне определяет линейное
однородное уравнение со старшим коэффициентом, равным единице.
Решим теперь такую задачу:
Дана фундаментальная система (в интервале 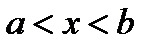 ): у1 , у2 , … , уп ; построить
): у1 , у2 , … , уп ; построить
соответствующее дифференциальное уравнение.
Для этой цели приравниваем нулю следующий определитель, в котором у обозна-
чает искомую функцию:
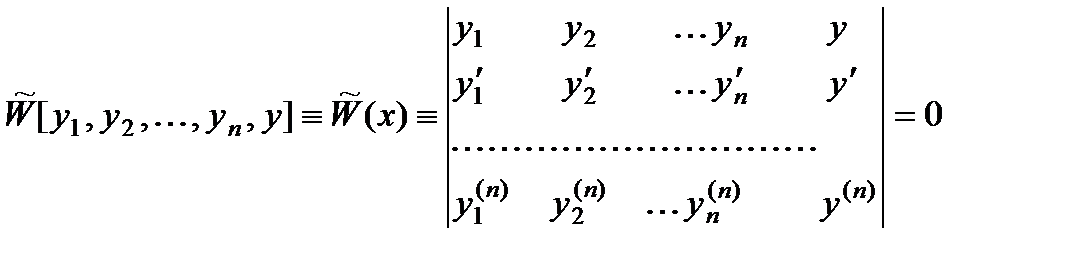 . (2)
. (2)
Разлагая его по элементам последнего столбца, мы убеждаемся в том, что равенство (2) представляет собой однородное дифференциальное уравнение п-го порядка относительно функции у. При подстановке вместо у функций уi (i = 1, 2, …, п) мы получаем определитель с двумя равными столбцами. Он тождественно равен нулю; следовательно, уравнение (2) допускает частные решения у1 , у2 , … , уп .
П р и м е р 14. Построить уравнение, имеющее в качестве фундаментальной системы функции х, х2, х3. Строим уравнение по формуле (2):
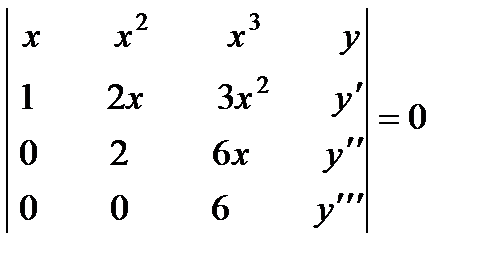 .
.
Раскрывая определитель по элементам последнего столбца, получаем:
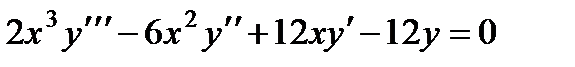 .
.
Здесь 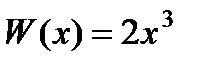 и не обращается в нуль в интервалах
и не обращается в нуль в интервалах 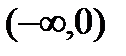 и
и 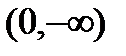 . Для этих интервалов имеем дифференциальное уравнение:
. Для этих интервалов имеем дифференциальное уравнение:
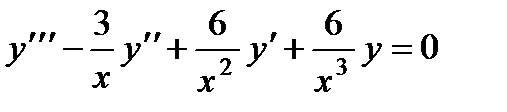 .
.
§ Понижение порядка линейного однородного уравнения
1. Для линейного однородного уравнения (1) справедлива формула Остроградского –
Лиувилля:
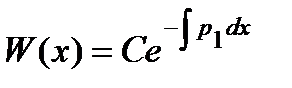 .
.
Применим ее к нахождению общего решения уравнения второго порядка:
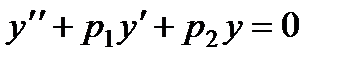 ,
,
у которого нам известно одно частное решение у1.
Пусть у есть любое решение этого уравнения, отличное от у1. Составляем
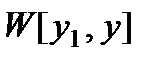 и записываем его значение по формуле Остроградского – Лиувилля:
и записываем его значение по формуле Остроградского – Лиувилля:
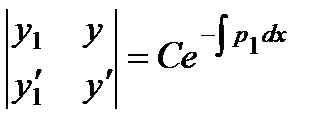 .
.
Раскрывая определитель, имеем линейное уравнение первого порядка:
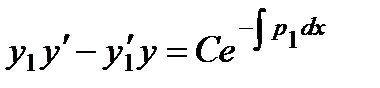 ;
;
делим обе части на 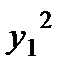 , находим:
, находим:
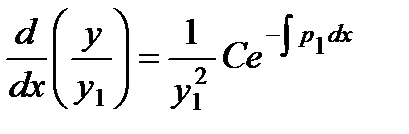 ,
,
откуда у определяется квадратурой:
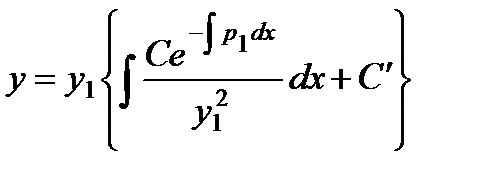 .
.
Полученное решение содержит два произвольных постоянных и, следовательно, является общим.
Итак, если известно одно частное решение линейного однородного уравнения
второго порядка, общее решение находится квадратурами.
Примечание. При решении задач пользоваться готовой квадратурой не рекоменду-
ется. Следует повторить ход решения.
П р и м е р 15. Проинтегрировать уравнение 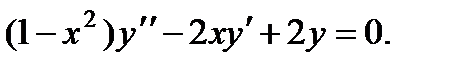
Легко убедиться, что частным решением этого уравнения является у1 = х. В нашем случае 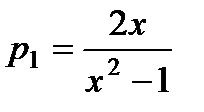 . Применяем формулу Остроградского – Лиувилля:
. Применяем формулу Остроградского – Лиувилля:
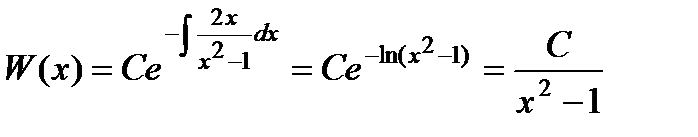 .
.
Теперь раскрываем выражение 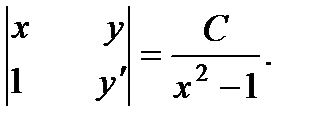 Откуда
Откуда 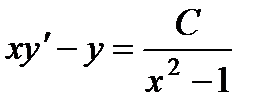 . Получилось линейное уравнение первого порядка, интегрируя которое, находим:
. Получилось линейное уравнение первого порядка, интегрируя которое, находим:
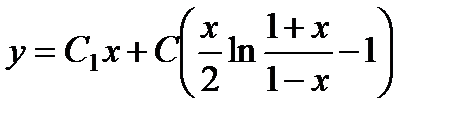 .
.
2. Понижение порядка в уравнении (1) при известном частном решении у1(х) можно
произвести с помощью подстановки у = у1z , где z – новая неизвестная функция.
В результате этой подстановки для z получим опять уравнение порядка п ,
которое не будет содержать неизвестной функции z , и, как следует из раздела 3.1, подстановка 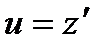 понижает порядок в уравнении для и на единицу.
понижает порядок в уравнении для и на единицу.
П р и м е р 16. Найти общее решение уравнения 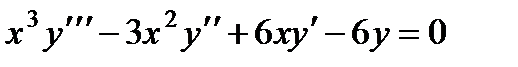 .
.
Легко находим частное решение у1 = х. Подстановка у = хz приводит к уравнению третьего порядка для z : 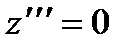 , которое легко интегрируется последовательным понижением порядка, в результате чего находим
, которое легко интегрируется последовательным понижением порядка, в результате чего находим
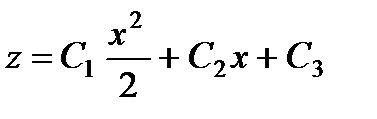 .
.
Так как у = хz , то окончательно 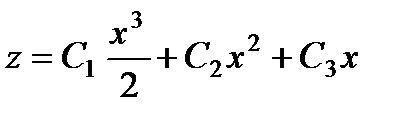 .
.
4.2 Линейное неоднородное дифференциальное уравнение
Рассмотрим неоднородное линейное дифференциальное уравнение вида:
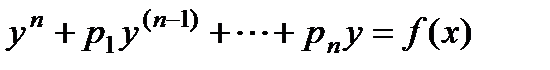 . (3)
. (3)
Однородное линейное уравнение с теми же коэффициентами, но с правой частью,
равной нулю, называется однородным уравнением, соответствующим неоднородному уравнению (3).
Т е о р е м а 1. Если известно какое-нибудь частное решение Y неоднородного уравнения (3), то общее его решение есть сумма этого частного решения и общего решения соответствующего однородного уравнения, т.е. 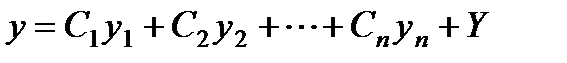 .
.
Здесь 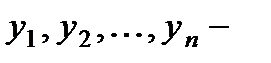 фундаментальная система решений соответствующего однородного уравнения.
фундаментальная система решений соответствующего однородного уравнения.
П р и м е р 17. Найти общее решение уравнения 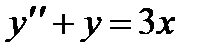 .
.
Легко видеть, что его частным решением будет у = 3х. Соответствующее однородное уравнение 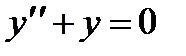 имеет фундаментальную систему решений:
имеет фундаментальную систему решений: 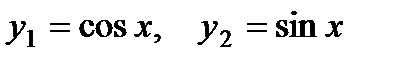 . В силу вышеприведенной теоремы, общим решением исходного уравнения будет
. В силу вышеприведенной теоремы, общим решением исходного уравнения будет
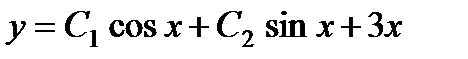 .
.
Т е о р е м а 2. Если известна фундаментальная система решений соответствую-
щего однородного уравнения, то общее решение неоднородного уравнения может быть найдено при помощи квадратур (методом вариации произвольных постоянных).
Решение неоднородного уравнения (3) ищется в виде:
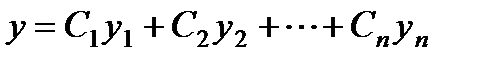 ,
,
где 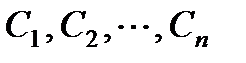 будут функциями независимого переменного х, которые определяются из следующей системы уравнений:
будут функциями независимого переменного х, которые определяются из следующей системы уравнений:
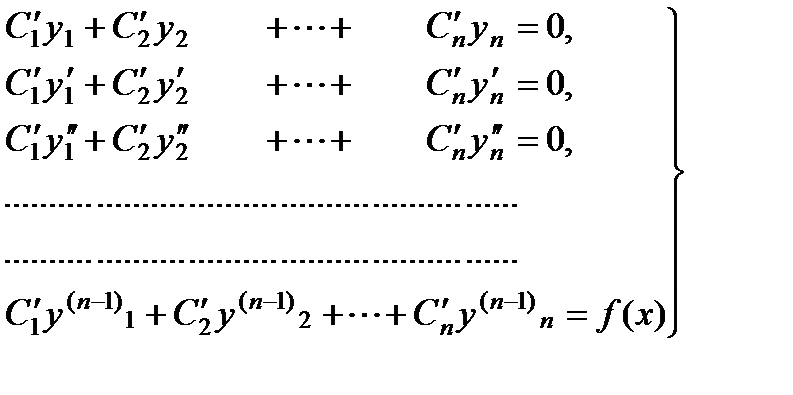 . (4)
. (4)
П р и м е р 18. Решить уравнение 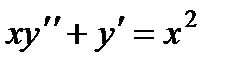 .
.
Решая однородное уравнение 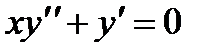 , получим:
, получим: 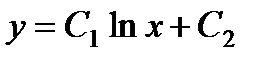 .
.
Следовательно, фундаментальная система решений имеет вид
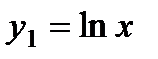 и
и 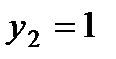 .
.
Составляем систему (4), учитывая, что канонический вид уравнения есть 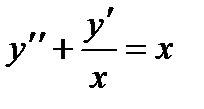 , т.е.
, т.е. 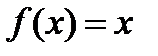 :
:
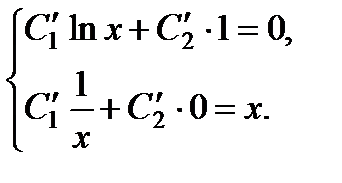
Отсюда
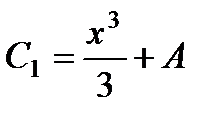 и
и 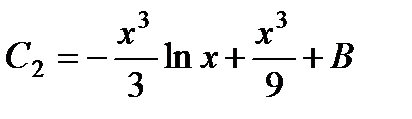
и, следовательно, по формуле 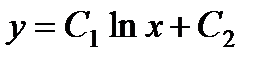 , окончательно находим:
, окончательно находим:
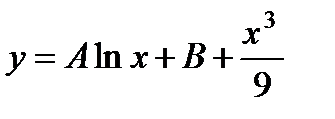 .
.
Последнее слагаемое в правой части есть не что иное, как частное решение исходного неоднородного уравнения.
4.3 Линейные уравнения с постоянными коэффициентами
4.3.1 Линейные однородные уравнения
Линейное однородное дифференциальное уравнение с постоянными
коэффициентами п-го порядка имеет вид
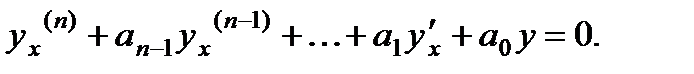 (1)
(1)
Общее решение этого уравнения определяется корнями характеристического уравнения
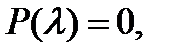 где
где 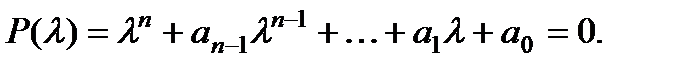 (2)
(2)
Возможны следующие случаи:
§ Все корни 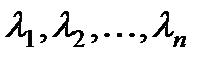 характеристического уравнения (2) действительны и различны. Тогда общее решение линейного однородного дифференциального уравнения (1) имеет вид
характеристического уравнения (2) действительны и различны. Тогда общее решение линейного однородного дифференциального уравнения (1) имеет вид
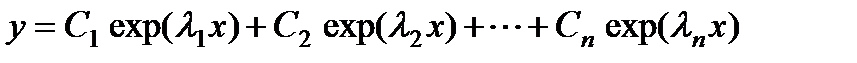 .
.
§ Имеется т равных действительных корней: 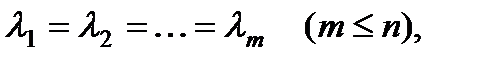 другие корни действительны и различны. В этом случае общее решение определяется формулой
другие корни действительны и различны. В этом случае общее решение определяется формулой
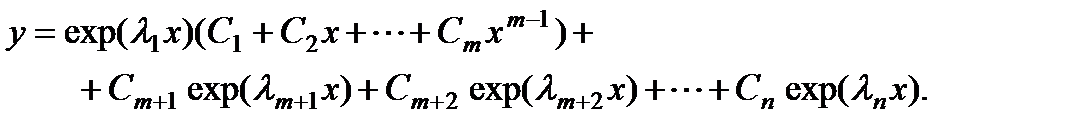
§ Имеется т равных комплексно сопряженных корней: 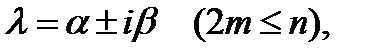 другие корни действительны и различны. В этом случае общее решение имеет вид
другие корни действительны и различны. В этом случае общее решение имеет вид
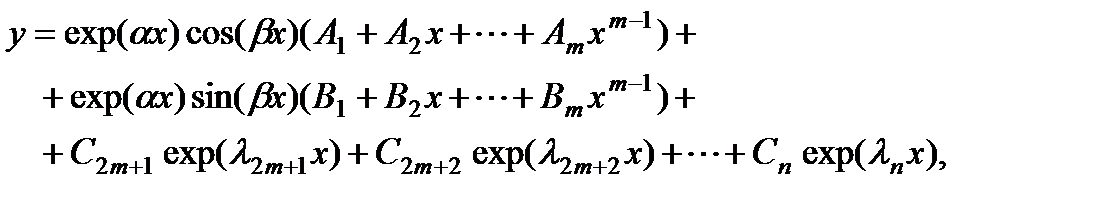
где 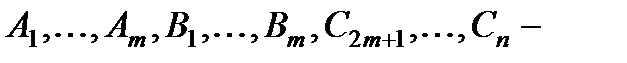 произвольные постоянные.
произвольные постоянные.
§ В общем случае, когда имеются r различных корней 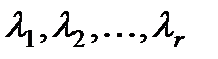 с кратностями
с кратностями 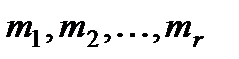 , левую часть характеристического уравнения (2) можно представить в виде произведения:
, левую часть характеристического уравнения (2) можно представить в виде произведения:
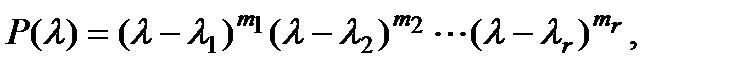
где 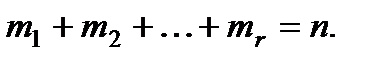 Общее решение исходного уравнения дается формулой
Общее решение исходного уравнения дается формулой
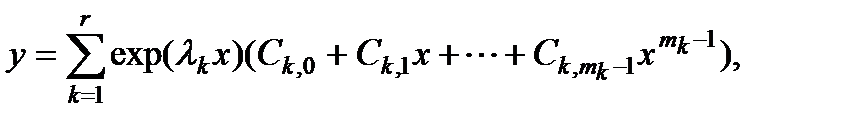
где 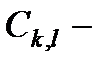 произвольные постоянные.
произвольные постоянные.
Если имеются комплексно сопряженные корни уравнения 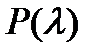 , то в указанном решении следует выделить действительную часть с учетом формулы:
, то в указанном решении следует выделить действительную часть с учетом формулы: 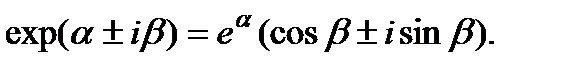
П р и м е р 19. Решить уравнение 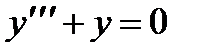 .
.
Его характеристическое уравнение 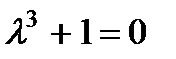 имеет корни
имеет корни
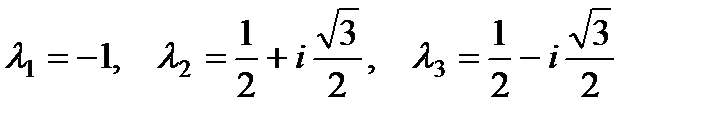 . Следовательно, фундаментальная система решений имеет вид:
. Следовательно, фундаментальная система решений имеет вид: 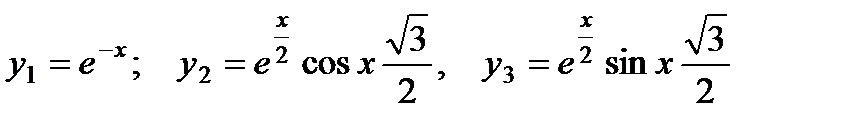 . Теперь записываем общее решение
. Теперь записываем общее решение
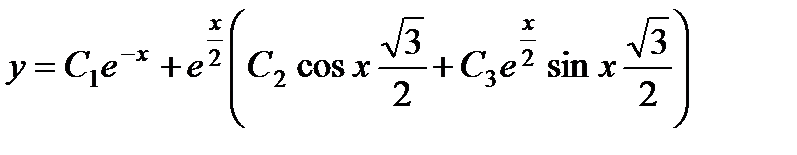 .
.
П р и м е р 20. Решить уравнение 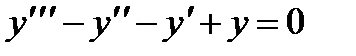 .
.
Его характеристическое уравнение 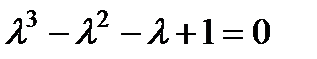 имеет корни
имеет корни 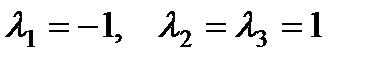 . Следовательно, фундаментальная система решений имеет вид:
. Следовательно, фундаментальная система решений имеет вид: 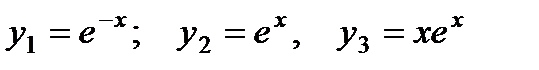 и окончательно общее решение:
и окончательно общее решение:
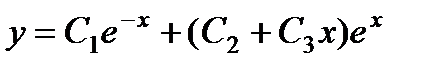 .
.
П р и м е р 21. Решить уравнение 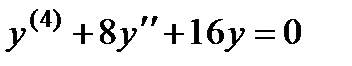 .
.
Его характеристическое уравнение 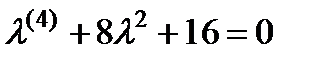 , которое можно переписать в виде
, которое можно переписать в виде 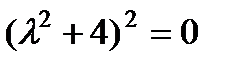 имеет корни
имеет корни 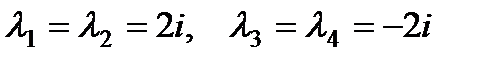 .
.
Общее решение:
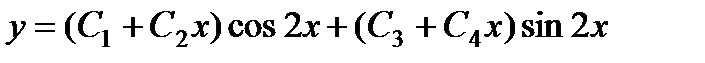 .
.
4.3.2 Линейные неоднородные уравнения
Когда найдено решение соответствующего однородного уравнения, т.е. известна
его фундаментальная система решений, то решение неоднородного уравнения согласно теореме 2 (разд. 4.2) находится в квадратурах.
Если правая часть неоднородного уравнения принадлежит к одному из указанных в
нижеследующей таблице типов, то решение неоднородного уравнения с постоянными коэффициентами может быть найдено вообще без интегрирования методом неопределенных коэффициентов.
В предлагаемой таблице перечислены типы правых частей уравнений и соответст-
вующие типы частных решений.
ТАБЛИЦА
Вид частных решений неоднородного уравнения с постоянными коэффициентами 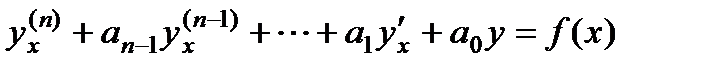 для правой части специального вида
для правой части специального вида
Вид правой части 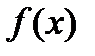 | Корни характеристического уравнения 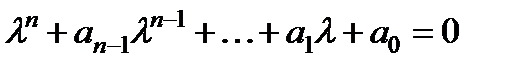 | Вид частного решения 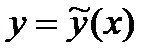 |
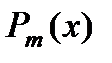 | Число 0 не является корнем характеристического уравнения | 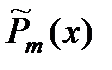 |
| Число 0 является корнем характеристического уравнения (кратности r) | 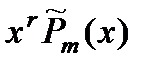 | |
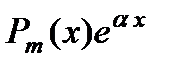 ( ( 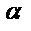 - действительное число) - действительное число) | Число 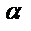 не является корнем характеристического уравнения не является корнем характеристического уравнения | 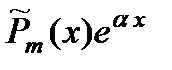 |
Число 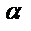 является корнем характеристического уравнения (кратности r) является корнем характеристического уравнения (кратности r) | 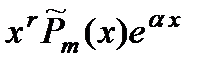 | |
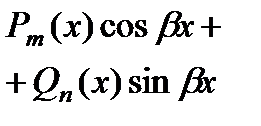 | Число 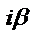 не является корнем характеристического уравнения не является корнем характеристического уравнения | 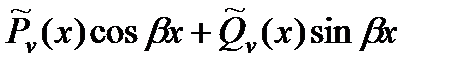 |
Число 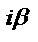 является корнем характеристического уравнения (кратности r) является корнем характеристического уравнения (кратности r) | 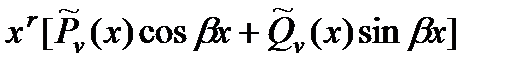 | |
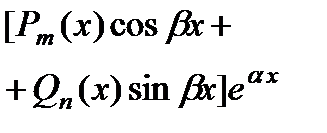  | Число 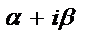 не является корнем характеристического уравнения не является корнем характеристического уравнения | 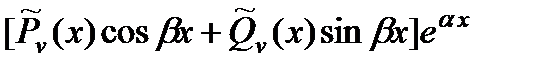 |
Число 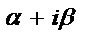 является корнем характеристического уравнения (кратности r) является корнем характеристического уравнения (кратности r) | 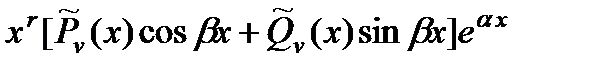 | |
Обозначения: 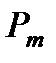 и и 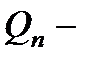 многочлены степени т и п с заданными коэффициентами; многочлены степени т и п с заданными коэффициентами; 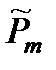 и и 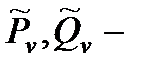 многочлены степени т и v, коэффициенты которых определяются в результате подстановки данного частного решения в исходное уравнение; v = max (m, n). многочлены степени т и v, коэффициенты которых определяются в результате подстановки данного частного решения в исходное уравнение; v = max (m, n). |
П р и м е р 22. Найти частное решение неоднородного уравнения 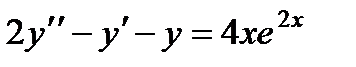 .
.
Характеристическое уравнение 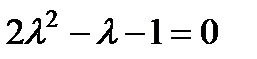 имеет корни
имеет корни 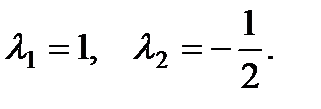 Правая часть уравнения
Правая часть уравнения 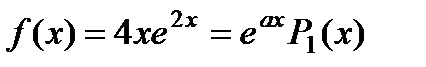 , где а = 2 не совпадает ни с одним из корней. Следовательно,
, где а = 2 не совпадает ни с одним из корней. Следовательно, 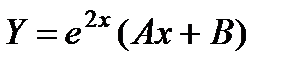 . Дифференцируя Y два раза и подставляя производные в данное уравнение, приравняв друг другу коэффициенты при первых степенях х и свободные члены в левой и правой частях полученного уравнения, имеем
. Дифференцируя Y два раза и подставляя производные в данное уравнение, приравняв друг другу коэффициенты при первых степенях х и свободные члены в левой и правой частях полученного уравнения, имеем 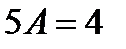 и
и 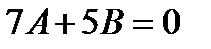 , откуда А = 4/5 и В = -28/25.
, откуда А = 4/5 и В = -28/25.
Таким образом, искомое частное решение 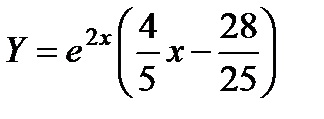 .
.
П р и м е р 23. Найти частное решение неоднородного уравнения 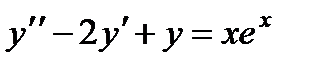 . Характеристическое уравнение
. Характеристическое уравнение 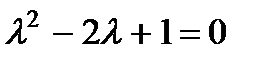 имеет двукратный корень
имеет двукратный корень 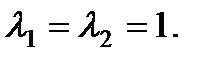 Правая часть уравнения
Правая часть уравнения 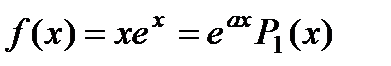 . Здесь а = 1 совпадает с двукратным корнем
. Здесь а = 1 совпадает с двукратным корнем 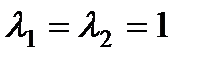 и, следовательно, т = 2. Таким образом, частное решение нужно искать в виде
и, следовательно, т = 2. Таким образом, частное решение нужно искать в виде 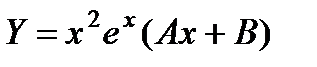 . Повторяя процедуру, описанную в предыдущем примере, А= 1/6 , В = 0. Следовательно, частное решение имеет вид
. Повторяя процедуру, описанную в предыдущем примере, А= 1/6 , В = 0. Следовательно, частное решение имеет вид 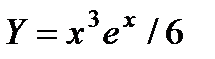 .
.
П р и м е р 24. Найти частное решение неоднородного уравнения 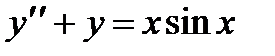 .
.
Характеристическое уравнение 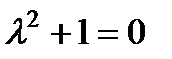 имеет корни
имеет корни 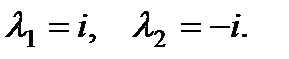 Правая часть уравнения имеет вид, указанный последним в левом столбце таблицы. Следовательно, частное решение нужно искать в виде
Правая часть уравнения имеет вид, указанный последним в левом столбце таблицы. Следовательно, частное решение нужно искать в виде 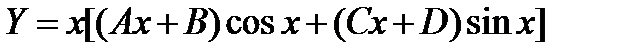 . Дифференцируя эту функцию два раза, подставляя в уравнение и приравнивая коэффициенты в обеих частях равенства при cos x, x cos x, sin x, x sin x получим четыре уравнения:
. Дифференцируя эту функцию два раза, подставляя в уравнение и приравнивая коэффициенты в обеих частях равенства при cos x, x cos x, sin x, x sin x получим четыре уравнения: 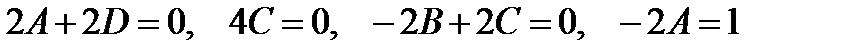 .
.
Отсюда находим 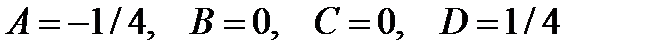 . Поэтому частное решение
. Поэтому частное решение
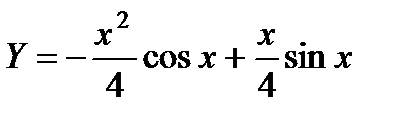 .
.
П р и м е р 25. Теперь рассмотрим пример с комбинированной правой частью:
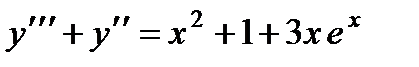 .
.
Обозначим 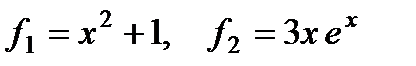 и будем искать частное решение в виде
и будем искать частное решение в виде 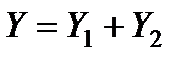 , т.е. находим частное решение двух уравнений:
, т.е. находим частное решение двух уравнений:
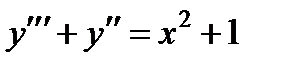 и
и 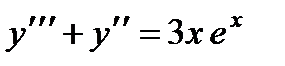 .
.
Характеристическое уравнение 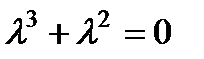 имеет корни
имеет корни 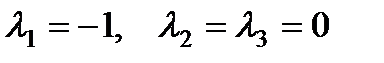 . Рассматривая каждое из последних уравнений изложенными выше методами, получим
. Рассматривая каждое из последних уравнений изложенными выше методами, получим 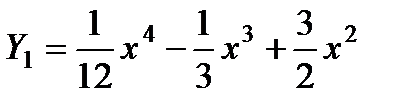 ;
; 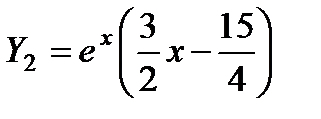 . Окончательно
. Окончательно
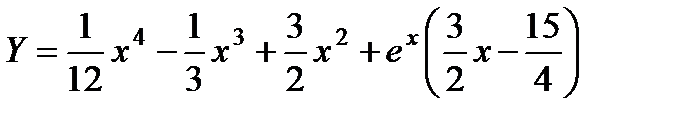 .
.
Если правая часть линейного уравнения с постоянными коэффициентами не имеет вида, приведенного в таблице и не является их линейной комбинацией, то для нахождения частного решения следует применить метод вариации произвольных постоянных.
ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Предлагается 25 вариантов индивидуальных заданий, включающих в себя
различные дифференциальные уравнения и две задачи на составление дифференциальных уравнений. Каждый вариант состоит из 8 заданий. Если в задании не указаны начальные условия, то следует найти общее решение заданного уравнения, а если к уравнению добавлены начальные условия, то следует решить задачу Коши. В седьмом и восьмом задании следует составить дифференциальное уравнение (исходя из условий задачи) и решить его.
Вариант 1
1. 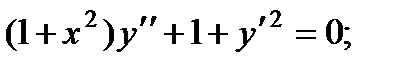
2. 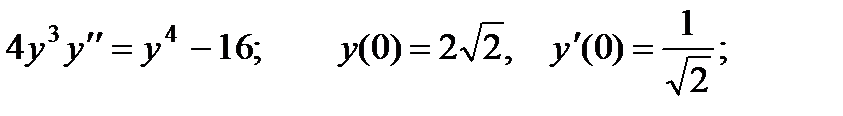
3. 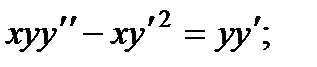
4. 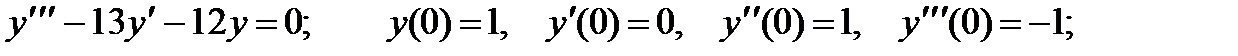
5. 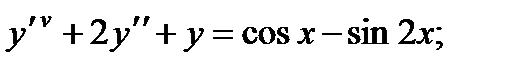
6. 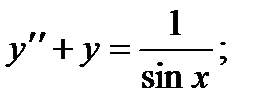
7. Два одинаковых груза подвешены к кольцу пружины. Найти закон движения одного из грузов, если другой оборвется. Дано, что удлинение пружины под влиянием одного из грузов равно а см.
8. Найти кривые, у которых в любой точке радиус кривизны вдвое больше отрезка нормали, заключенного между этой точкой кривой и осью абсцисс, если известно, что кривая обращена выпуклостью к оси ординат.
Вариант 2
1. 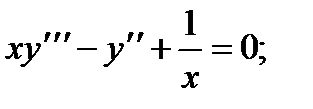
2. 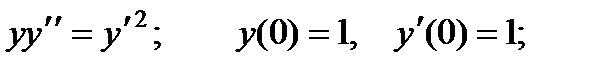
3. 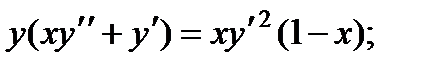
4. 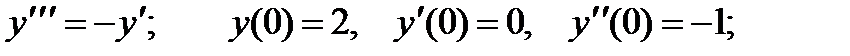
5. 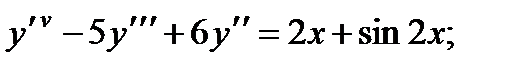
6. 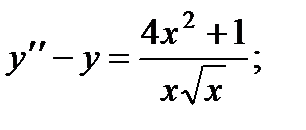
7. Последовательно включены источники тока, напряжение каждого меняется по закону 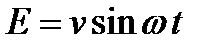 , сопротивление R и самоиндукция L. Найти силу тока в цепи (установившийся режим).
, сопротивление R и самоиндукция L. Найти силу тока в цепи (установившийся режим).
8. Найти плоские кривые, радиус кривизны которых пропорционален кубу длины отрезка нормали.
Вариант 3
1. 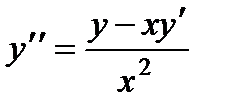
2. 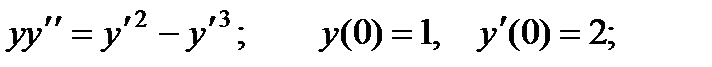
3. 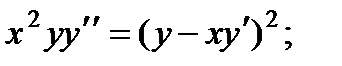
4. 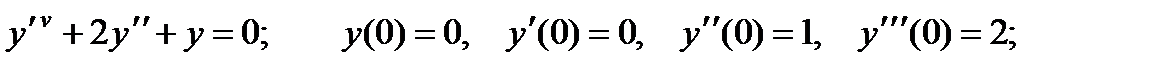
5. 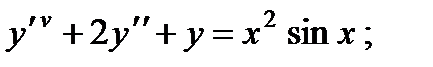
6. 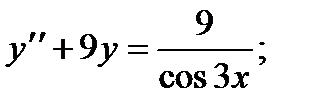
7. Найти кривые, у которых радиус кривизны равен нормали.
8. Материальная точка массы т движется прямолинейно к неподвижному центру, притягивающему ее силой, обратно пропорциональной кубу расстояния от точки до неподвижного центра. В начальный момент точка находится в покое и стоит от центра на расстоянии х0 . Определить время, по истечении которого точка достигает центра.
Вариант 4
1. 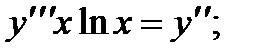
2. 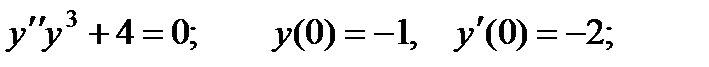
3. 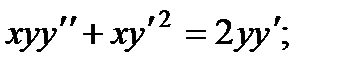
4. 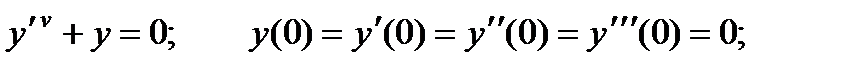
5. 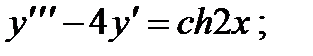
6. 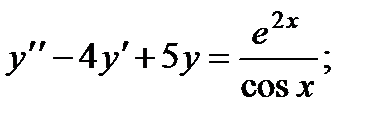
7. Найти линию, длина дуги которой, отсчитываемая от некоторой точки, пропорциональна угловому коэффициенту касательной в конечной точке дуги.
8. Материальная точка массы т движется прямолинейно под действием силы притяжения к неподвижному центру, пропорциональной расстоянию от точки до центра (k1 > 0). Сила сопротивления среды пропорциональна скорости (k2 > 0). В начальный момент времени точка находится на расстоянии а от центра, скорость равна v0 и направлена по прямой, соединяющей точку с центром. Найти закон движения, если (k22 < 4тk1).
Вариант 5
1. 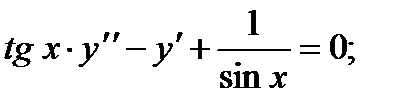
2. 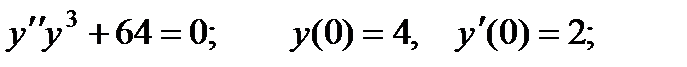
3. 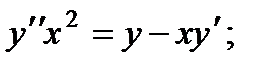
4. 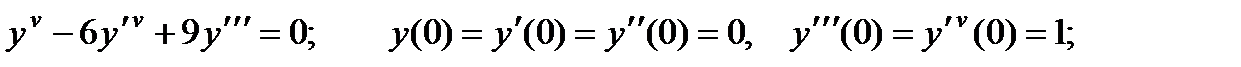
5. 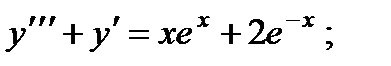
6. 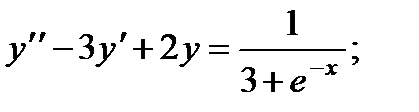
7. Найти кривые, у которых радиус кривизны есть данная функция 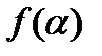 угла
угла 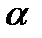 , образуемого касательной осью Ох ;
, образуемого касательной осью Ох ; 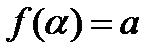 .
.
8. Тело массы т движется прямолинейно под действием постоянной силы F . Найти скорость движения тела и пройденный им путь, если в начальный момент времени они оба равны нулю, а сопротивление среды пропорционально квадрату скорости.
Вариант 6
1. 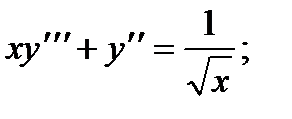
2. 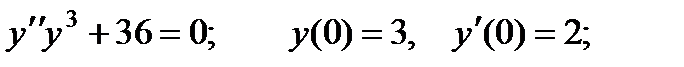
3. 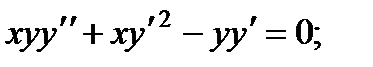
4. 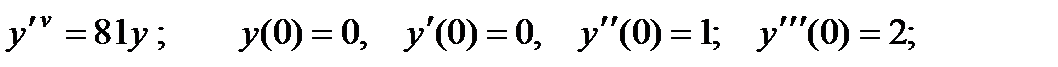
5. 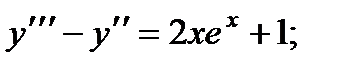
6. 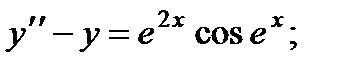
7. Найти кривые, у которых в любой точке радиус кривизны вдвое больше отрезка нормали, заключенного между этой точкой кривой и осью абсцисс, если известно, что кривая обращена выпуклостью к оси абсцисс.
8. Груз в Р кг подвешен на пружине и оттянул ее на а см. Затем пружина оттягивается еще на А см и отпускается без начальной скорости. Найти закон движения пружины, пренебрегая сопротивлением среды.
Вариант 7
1. 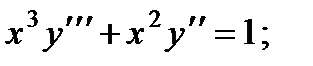
2. 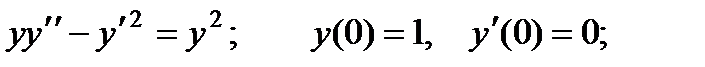
3. 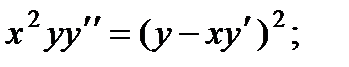
4. 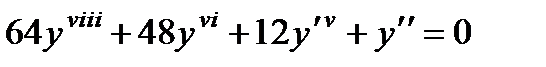
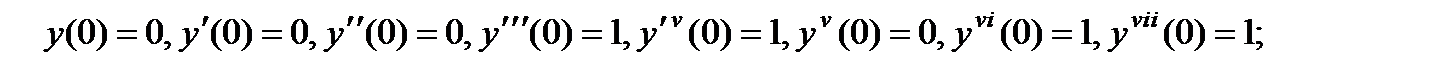
5. 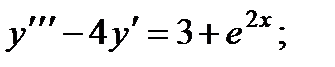
6. 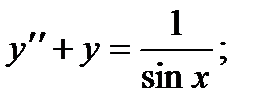
7. Найти интегральную кривую уравнения 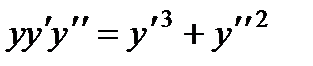 , касающуюся в начале координат прямой х + у =0.
, касающуюся в начале координат прямой х + у =0.
8. Электрическая цепь состоит из последовательно включенных источников постоянного тока, дающего напряжение U, сопротивления R, самоиндукции L и выключателя, который включается при t = 0. Найти зависимость силы тока от времени (при t > 0).
Вариант 8
1. 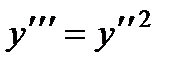 ;
;
2. 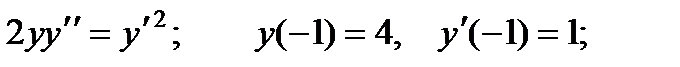
3. 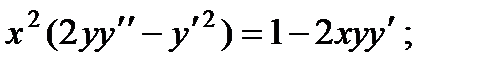
4. 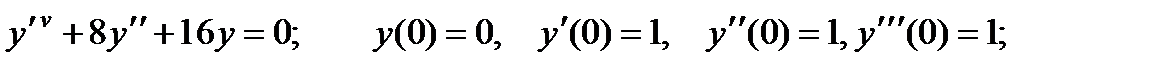
5. 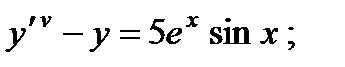
6. 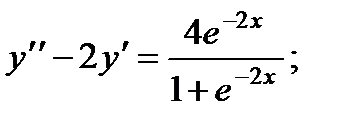
7. Найти кривые постоянного радиуса кривизны.
8. Найти закон прямолинейного движения материальной точка массы т под действием отталкивающей силы, обратно пропорциональной кубу расстояния от точки до неподвижного центра. В начальный момент точка находится в покое и отстоит от центра на расстоянии х0 .
Вариант 9
1. 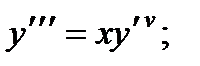
2. 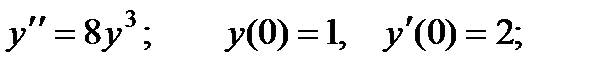
3. 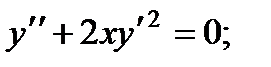
4. 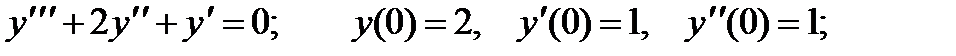
5. 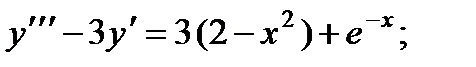
6. 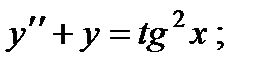
7. Найти линию, для которой проекция радиуса кривизны на ось Оу есть величина постоянная, равная 7.
8. Моторная лодка весом 300 кг движется прямолинейно с начальной скоростью
66 м/с . Сопротивление воды пропорционально скорости и равно 10 кг при скорости 1 м/с. Через какое время скорость лодки будет 8 м/с ?
Вариант 10
1. 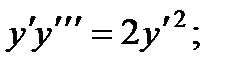
2. 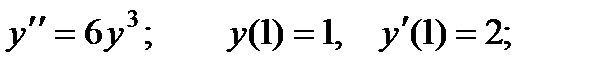
3. 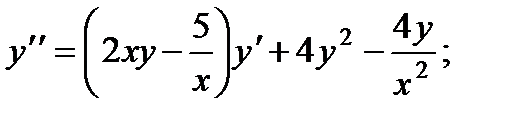
4. 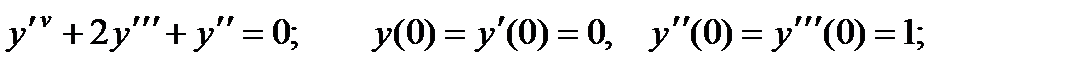
5. 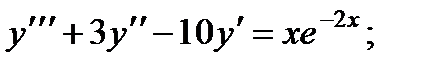
6. 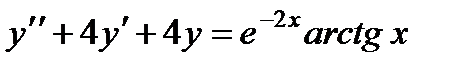 ;
;
7. При каких k и 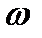 уравнение
уравнение 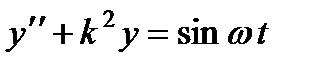 имеет хотя бы одно периодическое решение?
имеет хотя бы одно периодическое решение?
8. Материальная точка массы т движется прямолинейно под действием силы отталкивания от неподвижного центра, пропорциональной расстоянию от точки до центра (k1 > 0). Сила сопротивления среды пропорциональна скорости (k2 > 0). В начальный момент точка находится на расстоянии а от центра, скорость равна v0 и направлена по прямой, соединяющей точку с центром. Найти закон движения точки.
Вариант 11
1. 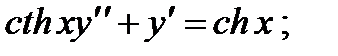
2. 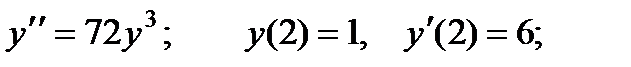
3. 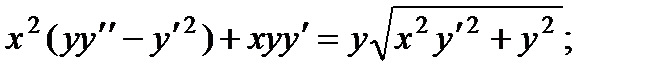
4. 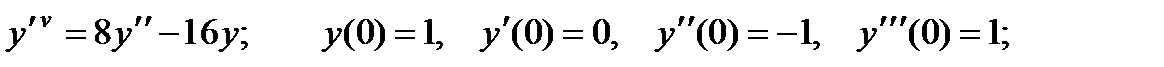
5. 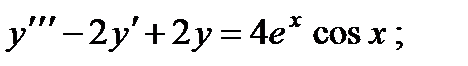
6. 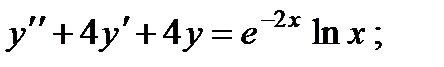
7. Составить дифференциальное уравнение семейства плоских кривых 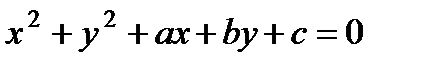 .
.
8. Цепь длиной 6м соскальзывает со стола. В момент начала движения со стола свисал 1м цепи. В течении какого времени со стола соскользнет вся цепь (трением пренебрегаем).
Вариант 12
1. 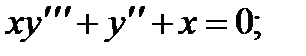
2. 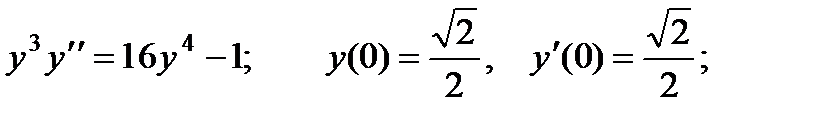
3. 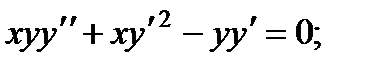
4. 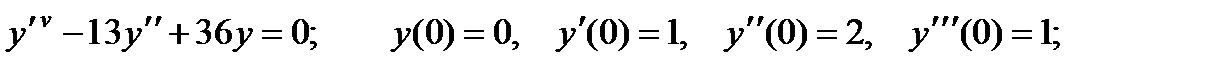
5. 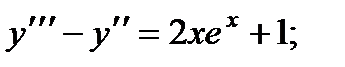
6. 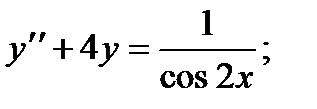
7. Найти интегральную кривую уравнения 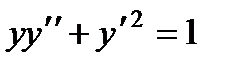 , проходящую через точку (0, 1) и касающуюся в этой точке прямой х + у = 1 (почему получается одна интегральная кривая?).
, проходящую через точку (0, 1) и касающуюся в этой точке прямой х + у = 1 (почему получается одна интегральная кривая?).
8. Частица массы т движется по оси Ох, отталкиваясь от точки х = 0 с силой 3mr0 и притягиваясь к точке х = 1 с силой 4mr1 , где r0 и r1 – расстояние до этих точек. Определить движения частицы с начальными условиями х(0) = 2, v(0) = 0.
Вариант 13
1. 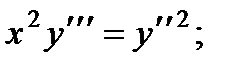
2. 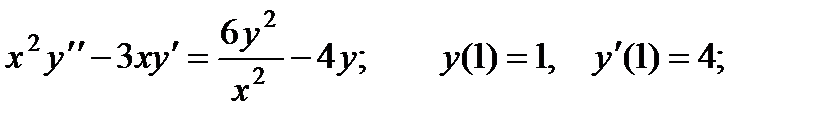
3. 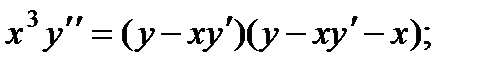
4. 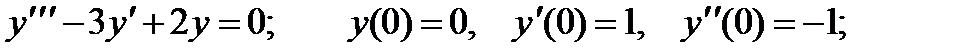
5. 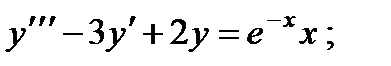
6. 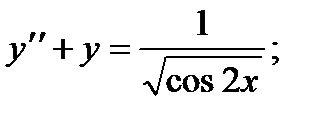
7. Найти уравнение кривых, у которых радиус кривизны в любой точке равен длине отрезка нормали заключенного между этой точкой и осью абсцисс, если кривая вогнута вниз.
8. Тело массы т движется прямолинейно под действием постоянной силы р. Найти скорость движения и пройденный им путь как функцию времени, если в начальный момент они оба равны нулю, а сопротивление среды пропорционально квадрату скорости.
Вариант 14
1. 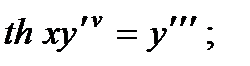
2. 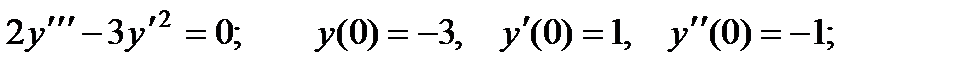
3. 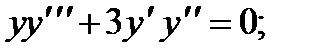
4. 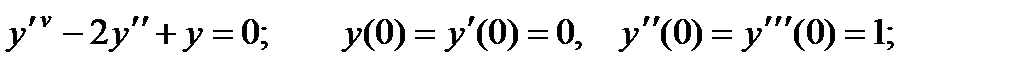
5. 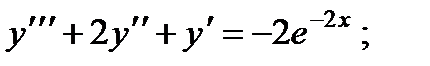
6. 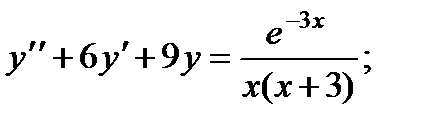
7. Найти кривые, у которых проекции радиуса кривизны на ось постоянны.
8. Тяжелое тело без начальной скорости скользит по наклонной плоскости. Найти закон движения, если угол наклона равен 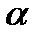 , а коэффициент трения
, а коэффициент трения 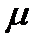 .
.
Указание: сила трения равна 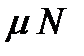 , где N – сила реакции плоскости.
, где N – сила реакции плоскости.
Вариант 15
1. 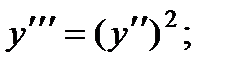
2. 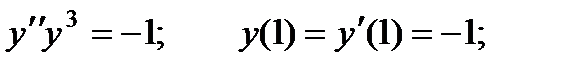
3. 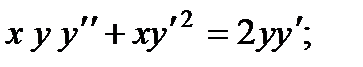
4. 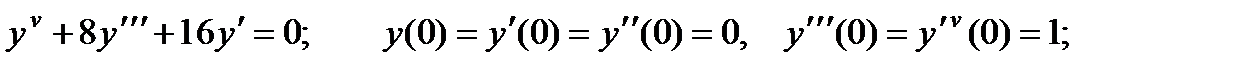
5. 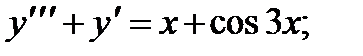
6. 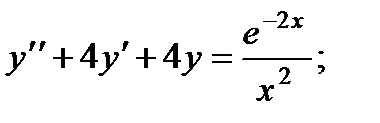
7. При каких а и b изо всех решений уравнения 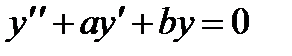 имеется хотя бы одно решение
имеется хотя бы одно решение 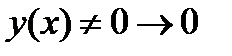 при
при 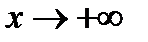 ?
?
8. Груз массой 4кг подвешен на пружине и увеличивает ее длину на 1см . Найти закон движения груза, если верхний конец пружины совершает гармоническое вертикальное колебание 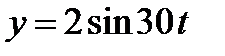 (см) и в начальный момент груз находился в покое (сопротивлением среды пренебречь).
(см) и в начальный момент груз находился в покое (сопротивлением среды пренебречь).
Вариант 16
1. 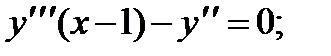
2. 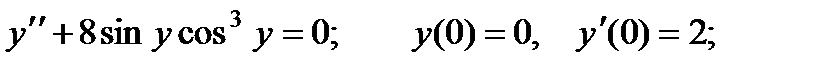
3. 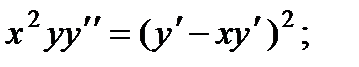
4. 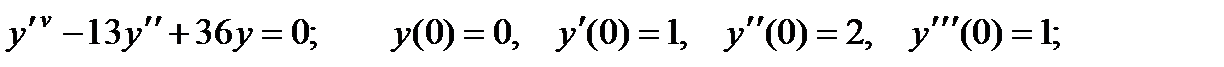
5. 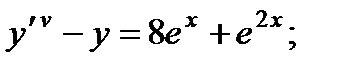
6. 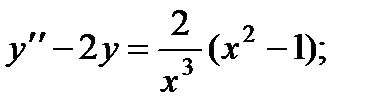
7. Найти форму равновесия однородной нерастяжимой нити под действием силы тяжести (цепная линия).
8. Найти закон движения тела, падающего без начальной скорости. Допуская, что сопротивление воздуха пропорционально квадрату скорости и что скорость имеет своим пределом при 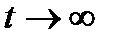 величину 75м/с.
величину 75м/с.
Вариант 17
1. 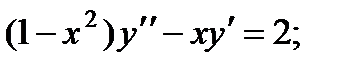
2. 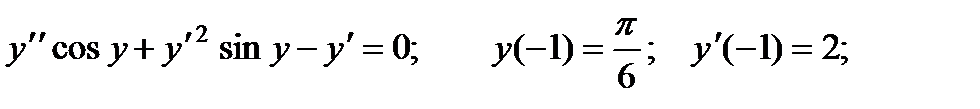
3. 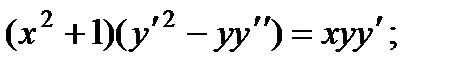
4. 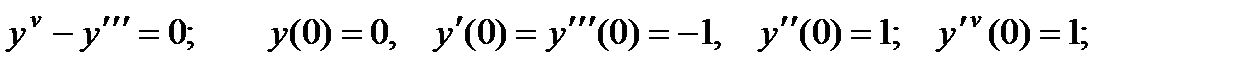
5. 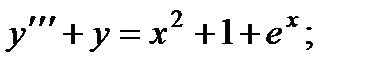
6. 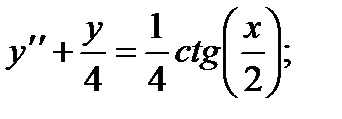
7. Определить формулу равновесия нерастяжимой нити с закрепленными концами, на которую действует нагрузка так, что на каждую единицу длины горизонтальной проекции нагрузка одинакова (цепи цепного листа). Весом самой нити пренебречь.
8. Материальная точка медленно погружается в жидкость. Найти закон движения, считая, что при медленном погружении сопротивление жидкости пропорционально скорости погружения.
Вариант 18
1. 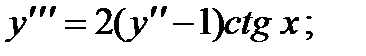
2. 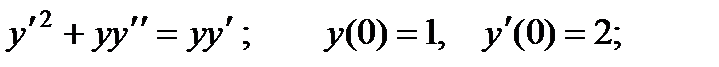
3. 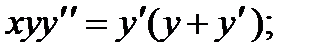
4. 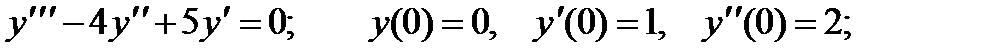
5. 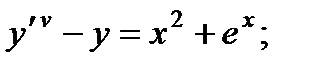
6. 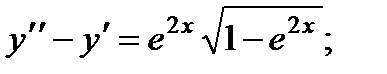
7. Найти уравнения кривых, у которых радиус кривизны в любой точке равен длине отрезка нормали, заключенного между этой точкой и осью абсцисс, если кривая вогнута вверх.
8. Мяч массой 400г падает с высоты 16,7м без начальной скорости. Сопротивление воздуха пропорционально скорости мяча и равно 0,0048Н при скорости 1м/с. Вычислить время падения и скорость мяча в конце падения. Принять g = 10м/с2.
Вариант 19
1. 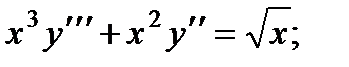
2. 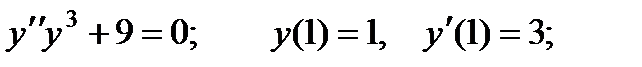
3. 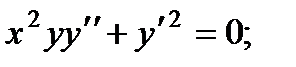
4. 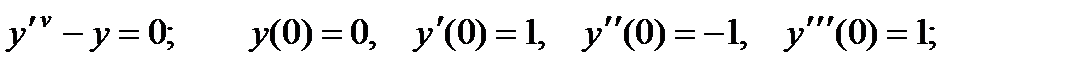
5. 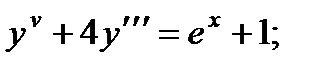
6. 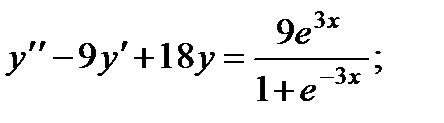
7. Найти кривую, у которой радиус кривизны вдвое больше нормали.
8. Балка длины l , встроенная правым концом в стену, изгибается силой р , приложенной к левому концу и равномерно распределенной нагрузкой q. Найти уравнение изогнутой балки и ее максимальный прогиб.
Вариант 20
1. 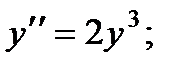
2. 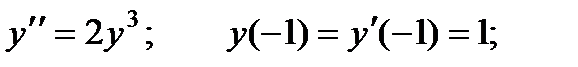
3. 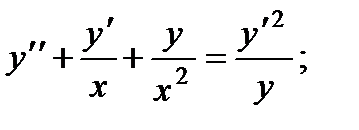
4. 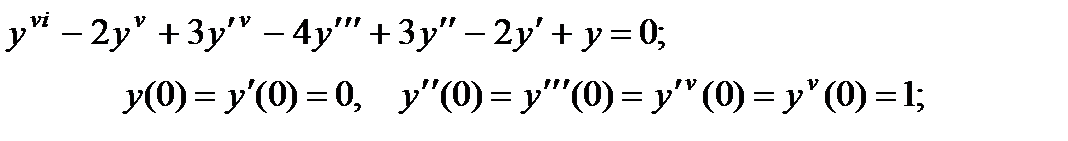
5. 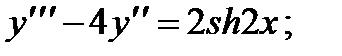
6. 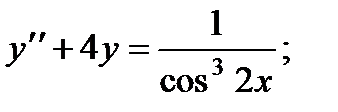
7. При каких а и b все решения уравнения 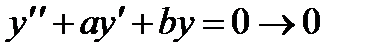 при
при 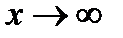 ?
?
8. Если тело медленно погружается в воду, то его скорость v и ускорение w приближенно связаны уравнением 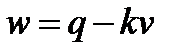 (q и k – const). Установить закон движения тела, если при t = 0, S = 0, v = 0.
(q и k – const). Установить закон движения тела, если при t = 0, S = 0, v = 0.
Вариант 21
1. 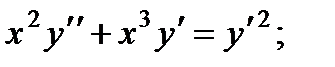
2. 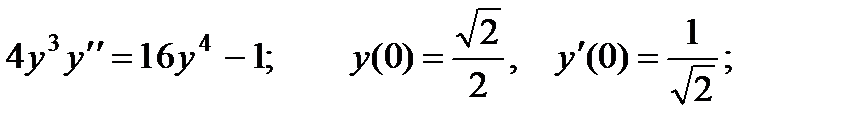
3. 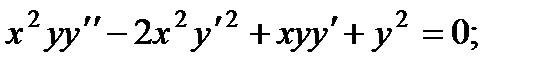
4. 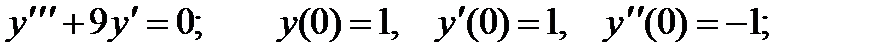
5. 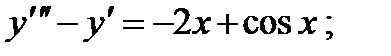
6. 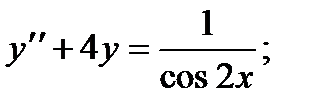
7. Найти плоские кривые, у которых радиус кривизны пропорционален длине отрезка нормали. Рассмотреть случаи, когда коэффициент пропорциональности k равен +1 , +2.
8. Найти скорость, с которой тело падает на поверхность Земли, если считать, что оно падает с бесконечно большой высоты и движение происходит только под влиянием притяжения Земли. Радиус Земли считать равным 6400км.
Вариант 22
1. 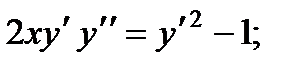
2. 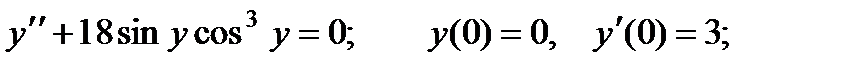
3. 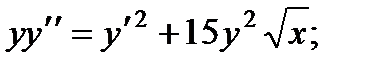
4. 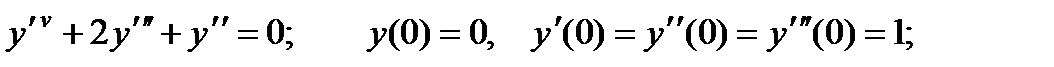
5. 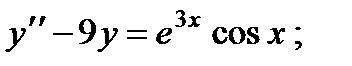
6. 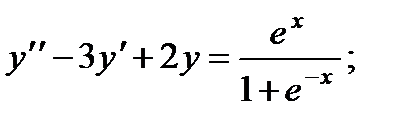
7. Найти кривые, у которых радиус кривизны обратно пропорционален косинусу угла между касательной и осью абсцисс.
8. Материальная точка массы т отталкивается от центра О с силой, пропор-циональной расстоянию. Сопротивление среды пропорционально скорости движения. Найти закон движения.
Вариант 23
1. 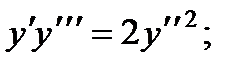
2. 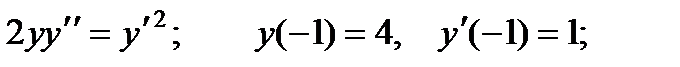
3. 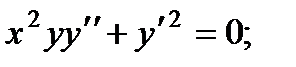
4. 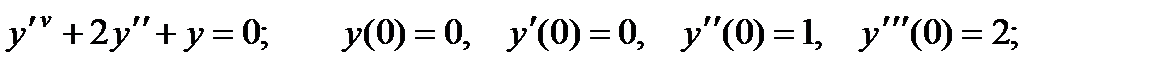
5. 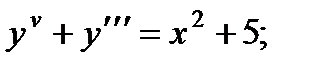
6. 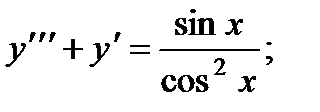
7. Найти уравнение кривой, касающейся оси абсцисс в начале координат, если ее кривизна в любой точке равна 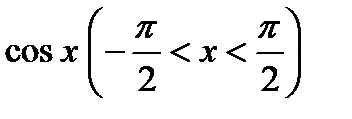 .
.
8. Найти закон движения тела, падающего в воздухе без начальной скорости, считая сопротивление воздуха пропорциональным квадрату скорости.
Вариант 24
1. 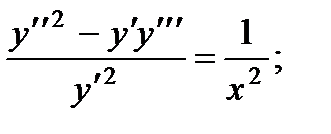
2. 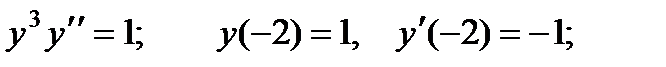
3. 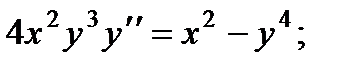
4. 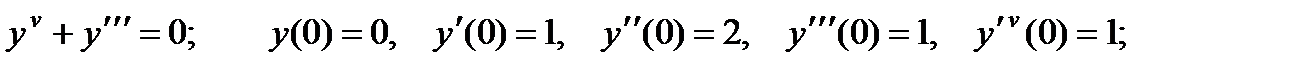
5. 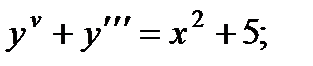
6. 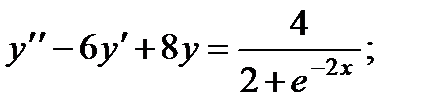
7. Найти кривую, у которой радиус кривизны пропорционален кубу нормали.
8. Балка длины l, лежащая концами на двух опорах, находится под действием равномерно распределенной нагрузки интенсивности q. Найти уравнение прогнутой оси балки и ее максимальный прогиб, выбрав начало координат в середине нагруженной балки.
Вариант 25
1. 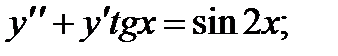
2. 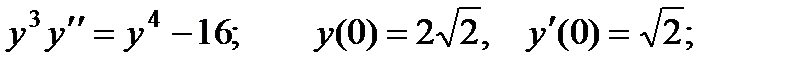
3. 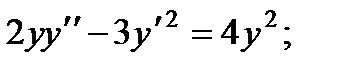
4. 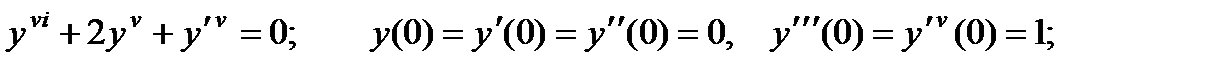
5. 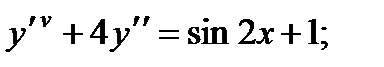
6. 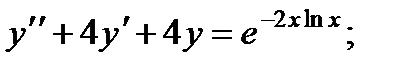
7. Найти кривые, у которых радиус кривизны пропорционален модулю радиус-вектора из начала координат до точки кривой.
8. Груз массы т покоится на упругой рессоре. На груз действуют восстанав-ливающая сила пропорциональная отклонению 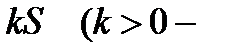 жесткость рессоры) и сила сопротивления, направленная в сторону против движения и пропорциональная скорости движения
жесткость рессоры) и сила сопротивления, направленная в сторону против движения и пропорциональная скорости движения 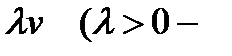 амортизатор). Записать уравнение движения.
амортизатор). Записать уравнение движения.
Список литературы
1. Егоров А.И. Обыкновенные дифференциальные уравнения с приложениями. – Физматлит, 2005.
2. Федорюк М.В. Обыкновенные дифференциальные уравнения. Издание 3 – URSS: 2009.
3. Задачи и упражнения по математическому анализу для ВТУЗов под редакцией Б.П. Демидовича. – М: «Интеграл – пресс», 1997.
4. Бабиков Ю.Н. Курс обыкновенных дифференциальных уравнений. – М: «Высшая школа», 1991.
5. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. – Ижевск: «РХД», 2000.
6. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. – М:Наука, 1980.
7. Арнольд В.И. Обыкновенные дифференциальные уравнения. – «Регулярная и хаотическая динамика», 2000.
Учебное издание
