Дисперсий воспроизводимости опыта

РАСЧЁТНО-ГРАФИЧЕСКОЕ ЗАДАНИЕ № 2

	Оптимизация буровых и горно-разведочных работ и

По дисциплине __________________________________________________________

___________________________планирование эксперимента_____________________

^{(наименование учебной дисциплины согласно учебному плану)}

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Полный факторный эксперимент 23

Тема:

_____________

_____________

Выполнил: студент гр. РТ-09 _____________ /Аллагузин З.Х./

^{(подпись) (Ф.И.О.)}

ОЦЕНКА:_______________

Дата: __________________

ПРОВЕРИЛ:

Руководитель проекта: ___________ /Страупник И.А./

^{(должность) (подпись) (Ф.И.О.)}

Санкт-Петербург

Условие задания

В ходе проведения экспериментальных исследований определялась механическая скорость бурения новой алмазной коронкой при изменении трех факторов: осевой нагрузки х₁, частоты вращения x₂ и расхода промывочной жидкости х₃. В качестве уровней факторов приняты крайние значения интервалов варьирования (табл. 1). Число параллельных опытов равнялось трем.

Таблица 1

Интервалы варьирования и уровни факторов

Факторы	Уровни факторов
–1	+1
x1, кН
x2, об/мин
x3, л/мин

План эксперимента с учетом взаимодействия факторов и его результаты приведены в табл. 2. Требуется построить математическую модель и проверить ее адекватность.

Таблица 2

План и результаты эксперимента

№ опыта	x0	x1	x2	x3	x1x2	x1x3	x2x3	х1x2x3	уIj, м/ч	уIIj, м/ч	уIIIj, м/ч
	+1	–1	–1	–1	+1	+1	+1	–1	0,33	0,4	0,36
	+1	+1	–1	–1	–1	–1	+1	+1	0,65	0,77	0,68
	+1	–1	+1	–1	–1	+1	–1	+1	0,48	0,58	0,5
	+1	+1	+1	–1	+1	–1	–1	–1	0,76	0,89	0,8
	+1	–1	–1	+1	+1	–1	–1	+1	0,38	0,46	0,39
	+1	+1	–1	+1	–1	+1	–1	–1	0,77	0,91	0,81
	+1	–1	+1	+1	–1	–1	+1	–1	0,55	0,67	0,59
	+1	+1	+1	+1	+1	+1	+1	+1	0,88	1,02	0,91

Рабочая матрица экспериментов

Проведем рандомизацию опытов (включая параллельные опыты), и определим возможный вариант рабочей матрицы экспериментов. Сначала введем последовательную нумерацию опытов: первому параллельному опыту первой серии опытов (1.1) присвоим номер 1; второму параллельному опыту первой серии (1.2) – номер 2; …; третьему параллельному опыту восьмой серии (8.3) – номер 24. Затем с использованием таблиц случайных чисел выберем произвольный порядок проведения экспериментов
(табл. 3). Для каждого опыта приведены конкретные значения факторов.

Таблица 3

Рабочая матрица экспериментов

№ п/п	№ опыта	x1, кН	x2, об/мин	x3, л/мин	y, м/ч
	7.2 = 20				0,67
	3.1 = 7				0,48
	5.2 = 14				0,46
	8.2 = 23				1,02
	1.2 = 2				0,4
	8.3 = 24				0,91
	2.2 = 5				0,77
	7.3 = 21				0,59
	4.2 = 11				0,89
	1.1 = 1				0,33
	7.1 = 19				0,55
	6.1 = 16				0,77
	8.1 = 22				0,88
	5.3 = 15				0,39
	2.1 = 4				0,65
	3.2 = 8				0,58
	2.3 = 6				0,68
	4.3 = 12				0,8
	6.3 = 18				0,81
	4.1 = 10				0,76
	5.1 = 13				0,38
	3.3 = 9				0,5
	1.3 = 3				0,36
	6.2 = 17				0,91

Первым проводится второй параллельный опыт седьмой серии экспериментов, вторым – первый параллельный опыт третьей серии и т.д. Результаты эксперимента приведены в правом крайнем столбце.

Определение уравнения регрессии

Найдем среднее значение результатов трех параллельных опытов по каждой строке матрицы планирования следующим образом:

(1)

и приведены в табл. 4.

Общий вид функции при учете взаимодействия факторов имеет следующий вид:

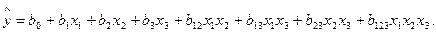(2)

Определим значения коэффициентов этого полинома:

;

;

;

;

;

;

;

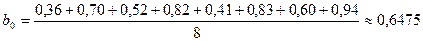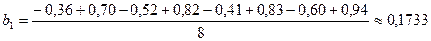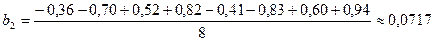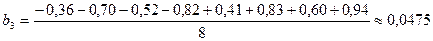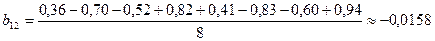
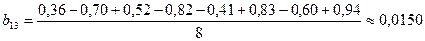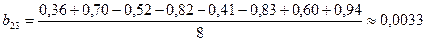Таблица 4

Результаты определения среднего значения параметра и

дисперсий воспроизводимости опыта

№ опыта	x0	x1	x2	x3	x1x2	x1x3	x2x3	x1x2x3	уIj, м/ч	уIIj, м/ч	уIIIj, м/ч	`yj, м/ч	10-3×s2j	y¢j, м/ч	Dy¢j, %
	+1	–1	–1	–1	+1	+1	+1	–1	0,33	0,4	0,36	0,36	1,23	0,3633	2,51
	+1	+1	–1	–1	–1	–1	+1	+1	0,65	0,77	0,68	0,70	3,90	0,6999	0,34
	+1	–1	+1	–1	–1	+1	–1	+1	0,48	0,58	0,5	0,52	2,80	0,5201	1,77
	+1	+1	+1	–1	+1	–1	–1	–1	0,76	0,89	0,8	0,82	4,43	0,8167	0,30
	+1	–1	–1	+1	+1	–1	–1	+1	0,38	0,46	0,39	0,41	1,90	0,4101	2,24
	+1	+1	–1	+1	–1	+1	–1	–1	0,77	0,91	0,81	0,83	5,20	0,8299	0,31
	+1	–1	+1	+1	–1	–1	+1	–1	0,55	0,67	0,59	0,60	3,73	0,6033	1,51
	+1	+1	+1	+1	+1	+1	+1	+1	0,88	1,02	0,91	0,94	5,43	0,9367	0,27

С учетом вычисленных коэффициентов математическая модель примет вид:

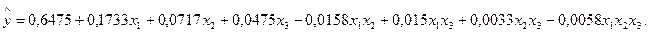
Проверка воспроизводимости результатов экспериментов

Для каждой строки плана рассчитаем дисперсию воспроизводимости опыта следующим образом:

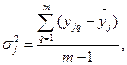(3)

ее значения также приведены в табл. 4.

Затем просуммируем дисперсии:

Выберем среди дисперсий наибольшую и определим G-критерий Кохрена:

( 4)

Табличное значение G-критерия Кохрена равно

G_{a=0,05, f1=2, f2=8}=0,5157.

Так как G<G_a,f1,f2, то можно сделать вывод о том, что с доверительной вероятностью 0,95 дисперсии опытов однородны, и гипотеза о воспроизводимости результатов экспериментов принимается.

Определяем дисперсию воспроизводимости всего эксперимента:

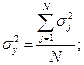. (5)

.

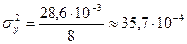Проверка значимости коэффициентов уравнения регрессии

Определяем общее количество опытов

L=8×3=24,

и находим дисперсию коэффициентов уравнения:

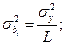(6)

.

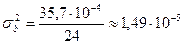Затем определяем среднеквадратичную ошибку, взяв квадратный корень из дисперсии коэффициентов уравнения:

.

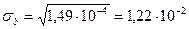Табличное значение t-критерия Стьюдента равно

t_{a=0,05; f=16}=2,119.

Тогда, доверительный интервал для коэффициентов уравнения определяется:

(7)

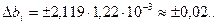
Коэффициенты уравнения являются незначимыми, если они находятся внутри доверительного интервала. Определяем, что незначимыми в полиноме являются b₂₃=0,0033 и b₁₂₃=–0,0058. Тогда уравнение, состоящее из значимых коэффициентов, имеет вид:

Вычислим по этому уравнению значения параметра, и занесем его в соответствующие строки табл. 4. Затем определим относительное отклонение вычисленных значений параметра по следующей формуле:

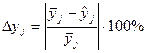(8)

и занесем результаты в табл. 4.

Максимальное относительное отклонение вычисленных значений параметра составляет 2,51 %.

Проверка адекватности модели

Рассчитаем дисперсию адекватности:

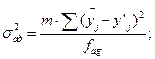(9)

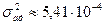
Число степеней свободы при этом f_ад=8-6=2, так как из восьми коэффициентов исходного уравнения значимых оказалось шесть.

Поскольку 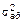£ 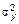, то можно сделать вывод об адекватности модели без проверки по F-критерию Фишера.

Анализ полученных результатов

Основное влияние на механическую скорость бурения оказывает осевая нагрузка, далее частота вращения, а затем расход промывочной жидкости. Увеличение всех факторов ведет к росту механической скорости бурения. Так как коэффициенты являются незначимыми, то при взаимодействие факторы х₂ и х₃ ; х₁ , х₂ и х₃ практически не влияют друг на друга. Факторы х₁ и х₂ ; х₁ и х₃ при взаимодействии оказывают друг на друга влияние.