Нижегородская (III открытая) городская математическая олимпиада школьников

г. Нижний Новгород, НФ ГУ ВШЭ, 18 декабря 2005 года

Класс

1. Решите уравнение sin x + cos x = tg x + ctg x. (К.Голубев, 11 кл., лицей №165, г.Н.Новгород) Ответ: данное уравнение корней не имеет. Решение: Заметим, что из свойств тангенса и неравенства Коши следует, что 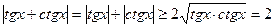. В то же время 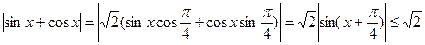. Получаем, что множество значений функции sin(x)+cos(x) по модулю не превосходит 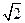, в то время, как множество значений tg(x)+ctg(x) по модулю не менее 2, значит, уравнение не имеет решений.

2. Новая шахматная фигура «лягушка» поочерёдно делает ходы на 1, 2, 3, 1, 2, 3, … клетки (по горизонтали или вертикали). Какое наибольшее количество клеток лягушка может посетить на доске 8´8 (без учёта исходной клетки), если ей нельзя вставать на клетки, на которых она уже была? (А.Смирнов, 1 курс, НФ ГУ ВШЭ &K)

3. Сколько решений имеет ребус 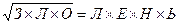? (одинаковые буквы – одинаковые цифры, разные буквы – разные цифры) (Д.Костерин, 11 кл., лицей №82, г.Н.Новгород)(Д.Костерин)

Ответ: 15120 решений. Решение: Если ни одна из букв не равна 0, то 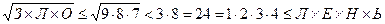,т.е. уравнение не имеет решений. Значит, уравнение имеет решение только тогда, когда обе части равны нулю, а это возможно только при Л=0, следовательно, остальные пять букв могут быть выбраны из 9 ненулевых цифр 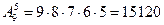способами.

4. AA₁, BB₁ и СC₁ – высоты остроугольного треугольника ABС. Точка D – проекция точки C₁ на высоту BB₁. Оказалось, что точки A₁, B₁, C₁, D лежат на одной окружности. Какие значения может принимать величина угла ВАС? (А.Куликов, 3 курс, НФ ГУ ВШЭ)

5. В стране 100 городов и не менее 1000 дорог между городами. Докажите, что туристическая компания имеет возможность организовать не менее 10 непересекающихся по дорогам циклических маршрутов. (Д.Васильев, 11 кл., гимназия №39, г.Уфа)

Нижегородская (III открытая) городская математическая олимпиада школьников

г. Нижний Новгород, НФ ГУ ВШЭ, 18 декабря 2005 года

Класс

1. За круглым столом сидят n³3 математиков (некоторые из которых смотрят внутрь, а некоторые – наружу), среди которых нет родившихся в один день. Каждый из них назвал 2 числа, равных 12d+31m, где d и m – соответственно день и месяц рождения каждого из его соседей. Можно ли по их ответам гарантированно определить день рождения каждого сидящего? (А.Маслов, 10 кл., шк. 85, г.Н.Новгород, Д.Мосунова, 8 кл., лицей №15, г.Саров)

2. Даны пять различных чисел а₁, а₂, а₃, а₄, а₅. Доказать, что для некоторых i и j выполняется неравенство: 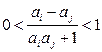. (П.Борискин, 10 кл., лицей №3, г.Саров)(П.Борискин)Решение: введём новые переменные 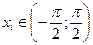такие, что a_i=tgx_i. Тогда данное нам выражение равно tg(x_i–x_j). Если упорядочить данные нам пять чисел, то среди четырёх промежутков между соседними числами по принципу Дирихле найдётся отрезок длиной, меньшей 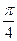, а тогда он и даст нам тангенс разности двух чисел, удовлетворяющий нужному нам неравенству.

3. Могло ли сохраниться множество простых делителей натурального числа n>10 после того, как в его десятичной записи поменяли местами две различные ненулевые цифры? (Е.Чернышов, 3 курс, ННГУ)

В треугольнике АВС ÐА=60°. Докажите, что 2ВС+АС>2АВ. (В.Шмаров, 10 кл., лицей №15, г.Саров) 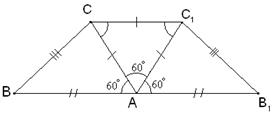Решение 1: Очевидно (см. рис.).

Решение 2: обозначим ВС=a, CA=b, AB=c, тогда по теореме косинусов a²=b²+c²–bc (*). Тогда нужное нам неравенство (2a+b>2c)Û(4a²+4ab+b²>4c²)Û (4b²+4c²–4bc+4ab+b²>4c²) с учётом (*) Û( 5b²–4bc+4ab>0)Û(5b+4a>4c), а это верное неравенство, т.к. следует из неравенства треугольника (a+b>c).

4. Существуют ли такие два многочлена ненулевых степеней P(x) и Q(x), что P(Q(x))+Q(P(x))=P(x)×Q(x)? (Е.Чернышов, 3 курс, ННГУ)

5. Фигура «лягушка» поочерёдно делает ходы на 1, 2, 3, 1, 2, 3, … клетки (по горизонтали или вертикали). Может ли лягушка обойти бесконечную клетчатую плоскость, побывав на каждой клетке ровно 1 раз? (А.Смирнов, 1 курс, НФ ГУ ВШЭ &K)