Приложение. Абсолютно упругий удар

При абсолютно упругом ударе выполняются законы сохранения импульса и механической энергии (E = const). Опыт показывает, что время удара очень мало, поэтому перемещением соударяющихся тел за это время можно пренебречь. Поэтому потенциальная энергия этих тел во внешнем силовом поле за время удара не изменяется, и суммарная кинетическая энергия тел до и после удара одинакова. В данной работе рассматривается прямой удар двух шаров, являющихся в силу их однородности центральным.

Рассмотрим процесс соударения. При сближении шаров, начиная с момента их первоначального соприкосновения, возрастают силы деформации, соответственно, возрастают и упругие силы, препятствующие деформациям. Скорости тел при этом изменяются, пока не станут равными. В этот момент деформации максимальны, максимальны и упругие силы взаимодействия. В системе отсчёта, где центр масс шаров покоится, полная кинетическая энергия шаров равна нулю, т. е. кинетическая энергия, которой обладали шары до соударения, полностью переходит в потенциальную энергию упругих деформаций шаров. Затем силы деформации расталкивают шары до тех пор, пока они не разойдутся. При этом потенциальная энергия деформаций шаров переходит обратно в их кинетическую энергию, шары восстанавливают свою форму и оказываются недеформированными. Реально процесс удара намного сложнее, так как при соударении в шарах возбуждаются упругие волны, распространяющиеся в шарах и после удара, поэтому кинетическая энергия шаров после удара меньше, чем до удара, на величину энергии этих волн. Ввиду малости энергии волн, как показывают расчёты, учитывать её не будем.

Запишем закон сохранения механической энергии для абсолютно упругого, прямого, центрального удара двух шаров:

(П-1)

h = 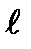(1 - cosα) , тогда

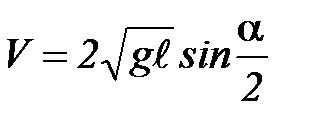(П-2)

При установлении связи между скоростью V и кинетической энергией (W_к) следует иметь в виду следующее. Движение шара является наложением поступательного движения по окружности и вращения вокруг оси, перпендикулярной плоскости движения и проходящей через центр шара с угловой скоростью ω. В этом случае кинетическая энергия складывается из энергии поступательного движения 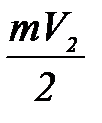и энергии вращательного движения 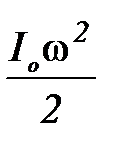, где I_o – момент инерции шара относительно оси, проходящей через его центр. Расчёт, однако, показывает, что неучёт энергии вращения даёт ошибку, не превышающую 1%, поэтому формула (П-1) достаточно верна.

Закон сохранения импульса для абсолютно упругого удара:

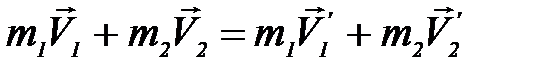
В нашем случаеV₂ = 0; m₁ = m₂ = m.

Найдём среднюю по времени силу, действующую на один из шаров.

По определению средняя сила равна:

,

где t_o – момент начала соударения;

t₁ – момент времени конца соударения;

– мгновенная сила взаимодействия шаров.

Согласно второму закону Ньютона:

, тогда ,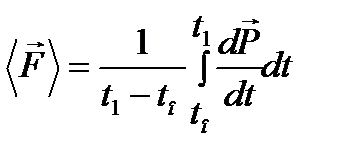

откуда

,

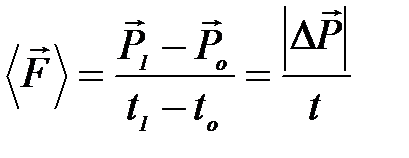здесь 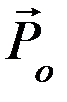– импульс шара до удара; – импульс шара после удара; – время соударения. Тогда модуль средней силы равен:

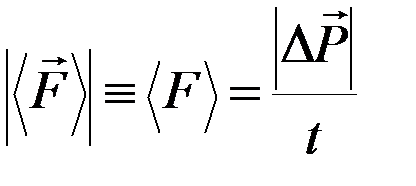
Если шары одинаковы и один из них до удара покоился, то можно показать, что налетающий шар после удара останавливается, а ранее покоящийся начинает движение с той скоростью, какую имел налетающий шар в момент начала удара. В этом случае для первоначально покоящегося шара имеем:

P_о = 0, P₁ = mV, где m – масса шара. Тогда

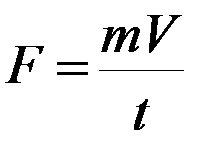(П-3)

Контрольные вопросы

1. Опишите упругий удар с точки зрения закона сохранения и превращения энергии.

2. Законы сохранения импульса и энергии требуют, чтобы налетающий шар остановился, а отскочивший имел ту же скорость, что и налетающий шар. Так ли это? Почему?

3. Почему шары подвешиваются так, что они должны соприкасаться и нити подвесов должны быть параллельны?

4. Могут ли скорости шаров после прямого центрального абсолютно упругого удара стать равными между собой?

5. Найти максимальную энергию упругой деформации шаров в данном случае.

6. Если шары имеют разные радиусы, но сделаны из одного и того же материала, то как зависит время соударения от большего радиуса.

7. Запишите законы сохранения для косого удара гладких шаров.