Тема 1. Множества, функции, отношения
Множества – основные понятия. Диаграммы Венна. Операции над множествами: объединение, пересечение, дополнение. Кортежи и прямое (декартово) произведение множеств. Соответствия и их свойства. Взаимно однозначные соответствия. Мощности бесконечных множеств. Принципы включений – выключений. Понятие функции. Обратные функции. Суперпозиции и формулы. Способы задания функций. Общее понятие отношения. Бинарные отношения и их свойства (рефлексивность, симметричность, транзитивность). Отношение эквивалентности и классы эквивалентности. Отношение порядка. Линейный порядок и частичный порядок. ([1, часть 2, кроме § 5, 6]; [2, разд. 1.1‒1.3]; [3, § 5.1, 13.1 – 13.3]).
Понятие множества относится к числу первичных, под которым понимается некоторая совокупность элементов, объединенных по каким-либо признакам. С множествами, их графическим изображением на диаграммах Венна студенты встречались ранее в курсах математического анализа и теории вероятностей. Там же рассматривались понятия подмножества В (части данного множества А: 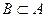 ), пустого множества
), пустого множества 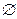 (не содержащего ни одного элемента), дополнения
(не содержащего ни одного элемента), дополнения 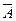 множества А (состоящего из всех элементов некоторого универсального множества[2] U, не входящих в множество А). Определялись основные операции над множествами А и В: объединение
множества А (состоящего из всех элементов некоторого универсального множества[2] U, не входящих в множество А). Определялись основные операции над множествами А и В: объединение 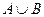 (множество, состоящее из всех элементов множества А и В), пересечение
(множество, состоящее из всех элементов множества А и В), пересечение 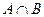 (множество, состоящее из всех общих элементов А и В), разность
(множество, состоящее из всех общих элементов А и В), разность 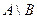 (множество, состоящее из всех элементов множества А, не входящих в множество В).
(множество, состоящее из всех элементов множества А, не входящих в множество В).
В данном курсе вводится понятие прямого, или декартова, произведения множеств А и В, т.е. множество 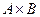 , элементы которого представляют всевозможные упорядоченные пары элементов множеств А и В (например, декартово произведение координатных осей Ох и Оу есть плоскость Оху).
, элементы которого представляют всевозможные упорядоченные пары элементов множеств А и В (например, декартово произведение координатных осей Ох и Оу есть плоскость Оху).
Множество называется конечным, если содержит конечное число элементов и – бесконечным в противном случае.
Если между множествами А и В имеет место взаимно однозначное соответствие (т.е. каждому элементу 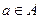 соответствует определенный элемент
соответствует определенный элемент 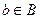 (
( 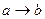 ) и наоборот (
) и наоборот ( 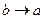 )), то говорят что множества А и В имеют одинаковую мощность или эквивалентны:
)), то говорят что множества А и В имеют одинаковую мощность или эквивалентны: 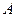 ~
~ 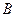 . Для конечных множеств это означает, что в них одинаковое число элементов. В случае бесконечного множества мощность является обобщением понятия «число элементов». В этом смысле счетные[3] множества являются «самыми маленькими» из бесконечных множеств.
. Для конечных множеств это означает, что в них одинаковое число элементов. В случае бесконечного множества мощность является обобщением понятия «число элементов». В этом смысле счетные[3] множества являются «самыми маленькими» из бесконечных множеств.
Пример 1. Даны множества чисел 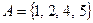 ,
, 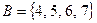 ,
, 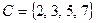 и универсальное множество
и универсальное множество 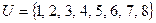 . Найти множества чисел:
. Найти множества чисел: 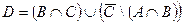 ;
; 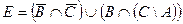 . Являются ли множества Е и D равными? эквивалентными? включающими одно в другое (
. Являются ли множества Е и D равными? эквивалентными? включающими одно в другое ( 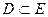 или
или 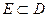 )? пересекающимися, но не включающими одно в другое? непересекающимися (
)? пересекающимися, но не включающими одно в другое? непересекающимися ( 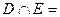
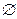 )?
)?
Р е ш е н и е. Для нахождения множества D вначале найдем: пересечения множеств 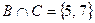 ,
, 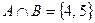 , дополнение множества С (до множества U)
, дополнение множества С (до множества U) 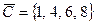 , разность множеств
, разность множеств 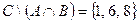 . Теперь
. Теперь 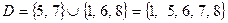 .
.
Для нахождения множества Е вначале найдем: 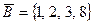 ,
, 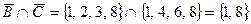 ,
, 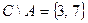 ,
, 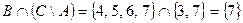 . Теперь
. Теперь 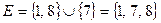 . Множества D и Е – не равные (так как не состоят из одинаковых элементов), не эквивалентные (так как имеют разные мощности (число элементов)), причем множество Е включается в множество D (
. Множества D и Е – не равные (так как не состоят из одинаковых элементов), не эквивалентные (так как имеют разные мощности (число элементов)), причем множество Е включается в множество D ( 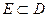 ). ►
). ►
Бинарным (двухместным) отношением множеств А и В называется любое подмножество R декартова множества 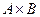 , т.е.
, т.е. 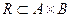 . Это означает, что если элементы х и у связаны бинарным отношением R (записываемым в виде xRy), то пара (х, у) является элементом R, т.е.
. Это означает, что если элементы х и у связаны бинарным отношением R (записываемым в виде xRy), то пара (х, у) является элементом R, т.е. 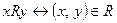 . Среди свойств бинарных отношений выделяют рефлексивность, симметричность, транзитивность ([1, часть 2, § 10]; [3, §13.3]). Бинарное отношение, для которого выполнены указанные три свойства, называется отношением эквивалентности, являющееся обобщением понятия равенства. Подмножества элементов, эквивалентные данному, называется его классом эквивалентности. Если бинарное отношение R на множестве Х рефлексивно, транзитивно и антисимметрично, то оно называется отношением порядка (отношением частичного порядка). Отношение частичного порядка называется линейным порядком, если для любых значений х и у имеет место либо xRy, либо уRх.
. Среди свойств бинарных отношений выделяют рефлексивность, симметричность, транзитивность ([1, часть 2, § 10]; [3, §13.3]). Бинарное отношение, для которого выполнены указанные три свойства, называется отношением эквивалентности, являющееся обобщением понятия равенства. Подмножества элементов, эквивалентные данному, называется его классом эквивалентности. Если бинарное отношение R на множестве Х рефлексивно, транзитивно и антисимметрично, то оно называется отношением порядка (отношением частичного порядка). Отношение частичного порядка называется линейным порядком, если для любых значений х и у имеет место либо xRy, либо уRх.
Соответствие 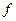 , сопоставляющее каждому элементу х множества Х один и только один элемент у множества Y, называется отображением множества Х на множество Y.
, сопоставляющее каждому элементу х множества Х один и только один элемент у множества Y, называется отображением множества Х на множество Y.
Функцией называется бинарное отношение 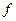 , если из
, если из 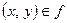 и
и 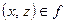 , следует, что
, следует, что 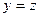 . Если область определения и область значений функции соответственно Х и Y, то говорят, что функция
. Если область определения и область значений функции соответственно Х и Y, то говорят, что функция 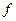 отображает множество Х на множество Y, т.е.
отображает множество Х на множество Y, т.е. 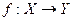 . Это означает, что для любого элемента
. Это означает, что для любого элемента 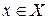 существует единственный элемент
существует единственный элемент 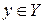 такой, что
такой, что 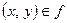 .
.
Подробнее о функциях говорилось в курсе «Математического анализа».
Важное значение в теории множеств имеет формула включений-выключений (принцип включений-выключений), позволяющая определить мощность объединения конечного числа конечных множеств. В простейших случаях (для двух или трех множеств) эта формула имеет вид:
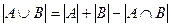 , (1)
, (1)
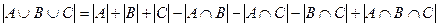 . (2)
. (2)
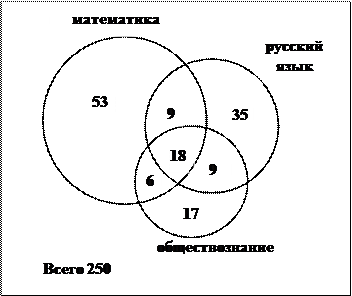
Пример 2. Из 250 абитуриентов экономического вуза, сдававших вступительные экзамены, отметку «3» получили: по математике 86 чел, по русскому языку – 71, обществознанию – 50, по математике или русскому языку – 130, по математике или обществознанию – 112, по русскому языку или обществознанию– 94, по всем трем предметам – 18 чел. Сколько абитуриентов сдали вступительные экзамены: а) без троек; б) с одной тройкой по математике; в) с одной тройкой.
Р е ш е н и е. а) Пусть 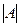 ,
, 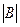 ,
, 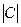 – число абитуриентов, получивших отметку «3» соответственно по математике, русскому языку и обществознанию. По условию
– число абитуриентов, получивших отметку «3» соответственно по математике, русскому языку и обществознанию. По условию 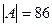 ,
,  ,
, 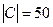 ,
, 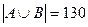 ,
, 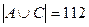 ,
, 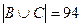 ,
, 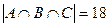 . Вначале найдем число абитуриентов, получивших оценку «3» по математике и русскому языку, т.е.
. Вначале найдем число абитуриентов, получивших оценку «3» по математике и русскому языку, т.е. 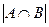 . Из формулы (1)
. Из формулы (1) 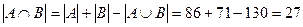 . Аналогично
. Аналогично 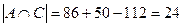 ,
, 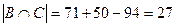 .
.
Теперь найдем число, абитуриентов, получивших оценку «3» хотя бы по одному из трех предметов, т.е. 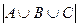 . По формуле (2)
. По формуле (2) 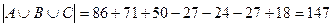 . Следовательно, число абитуриентов, сдавших вступительные экзамены без троек, равно 250–147=103 (чел).
. Следовательно, число абитуриентов, сдавших вступительные экзамены без троек, равно 250–147=103 (чел).
 б) Вначале найдем число абитуриентов, имеющих только две тройки – по математике и русскому языку:
б) Вначале найдем число абитуриентов, имеющих только две тройки – по математике и русскому языку: 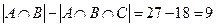 , по математике
, по математике
и обществознанию: 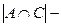 Следовательно, только одну тройку по математике имеют 86– –9–6–18=53 (чел).
Следовательно, только одну тройку по математике имеют 86– –9–6–18=53 (чел).
в) Аналогично п. б) найдем число абитуриентов, имеющих только одну тройку по русскому языку: 71– (27–18) –(27–18) –18=35 (чел) и по обществознанию:50–(24– –18) – (27–18) –18=17 (чел). Всего абитуриентов, имеющих только одну тройку, равно 53+35+17=105
(чел). Решение задачи легко иллю-
Рис. 1 стрируется на диаграмме Венна. (рис.1)►
Тема 2. Комбинаторика
Предмет комбинаторики. Правило суммы и правило произведения. Размещения, перестановки, сочетания без повторений и с повторениями. Биномиальные коэффициенты и соотношения для них. Задачи перечисления. Подсчет числа функций с конечными областями определения. ([1, часть 3]; [2, разд. 3.1]); [3, § 1.5]).
Комбинаторика – раздел математики, изучающий методы решения задач, связанных с выбором и расположением частей конечного множества, в частности, комбинаторных задач на подсчет числа различных комбинаций.
Студенты должны четко знать правила комбинаторики:
- правило суммы: если объект 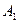 может быть выбран
может быть выбран 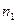 способами,
способами, 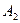 – другими
– другими 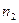 способами, то выбор одного из объектов
способами, то выбор одного из объектов 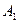 или
или 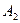 может быть осуществлен
может быть осуществлен 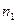 +
+ 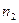 способами;
способами;
- правило произведения: если объект 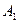 может быть выбран
может быть выбран 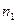 способами, после каждого такого выбора объект
способами, после каждого такого выбора объект 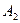 может быть выбран
может быть выбран 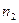 способами, то выбор всех объектов
способами, то выбор всех объектов 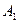 ,
, 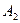 в указанном порядке может быть осуществлен
в указанном порядке может быть осуществлен 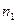
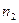 способами.
способами.
Из множества 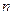 различных элементов могут быть образованы подмножества (комбинации) из
различных элементов могут быть образованы подмножества (комбинации) из 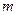 элементов
элементов 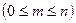 .
.
Если комбинации из 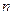 элементов по
элементов по 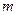 отличаются, либо составом элементов, либо порядком их расположения (либо и тем и другим), то их называют размещениями. Число размещений из
отличаются, либо составом элементов, либо порядком их расположения (либо и тем и другим), то их называют размещениями. Число размещений из 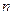 элементов по
элементов по 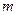 находятся по формуле:
находятся по формуле:
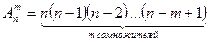 или
или 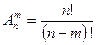 .
.
(где 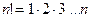 ).
).
Если комбинации из 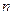 элементов по
элементов по 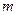 отличаются только составом элементов, то их называют сочетаниями. Число сочетаний из
отличаются только составом элементов, то их называют сочетаниями. Число сочетаний из 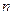 элементов по
элементов по 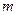 находятся по формуле:
находятся по формуле:
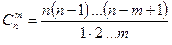 или
или 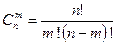 .
.
Свойства числа сочетаний:
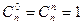 (ибо
(ибо 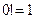 ),
), 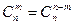 .
.
Если комбинации из 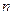 элементов отличаются только порядком элементов, то их называют перестановками. Число перестановок из
элементов отличаются только порядком элементов, то их называют перестановками. Число перестановок из 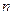 элементов находится по формуле:
элементов находится по формуле:
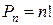
Пример 3.В первом туре конкурса участвуют 16 человек. Сколько существует различных исходов этого тура, при которых совпадают участники, занявшие призовые 1-е, 2-е и 3-е места, а также два участника, занявшие 15-е и 16-е места и выбывающие из дальнейшего участия в конкурсе?
Р е ш е н и е. Способы распределения участников, занявших 1-е, 2-е и 3-е места (из 16), отличаются как составом участников, так и их порядком; их число – число размещений 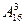 . Из оставшихся
. Из оставшихся 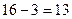 участников два выбывают из конкурса (порядок этих участников значения не имеет); их число – число сочетаний
участников два выбывают из конкурса (порядок этих участников значения не имеет); их число – число сочетаний 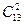 . По правилу произведения (см. с. 8) получаем, что число различных исходов первого тура конкурса, удовлетворяющих условию задачи, есть
. По правилу произведения (см. с. 8) получаем, что число различных исходов первого тура конкурса, удовлетворяющих условию задачи, есть
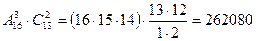
(или 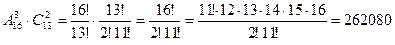 ).
).
Другой способ решения состоит в том, что общее число различных исходов первого тура с 16-ю участниками (без учета распределения тех или иных мест) равно числу перестановок 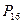 . Перестановки участников, занявших места с 4-го по 14-е (т.е. 11 мест), а также 15-е и 16-е места (2 места) приводят к совпадающему в соответствии с условием исходу первого тура; их число (по правилу произведения) равно
. Перестановки участников, занявших места с 4-го по 14-е (т.е. 11 мест), а также 15-е и 16-е места (2 места) приводят к совпадающему в соответствии с условием исходу первого тура; их число (по правилу произведения) равно 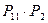 . Значит, число различных исходов первого тура конкурса, удовлетворяющих условию, есть
. Значит, число различных исходов первого тура конкурса, удовлетворяющих условию, есть
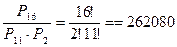 . ►
. ►
Если в комбинациях из 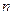 элементов часть элементов (или все) являются одинаковыми, то их называют комбинациями (размещениями, сочетаниями, перестановками) с повторениями.
элементов часть элементов (или все) являются одинаковыми, то их называют комбинациями (размещениями, сочетаниями, перестановками) с повторениями.
Соответствующие формулы таких комбинаций с повторениями, приведены в пособии ([1, часть 3]; [3, § 1.5]). Там же рассматриваются задачи на подсчет различных комбинаций [1, 1-ое практическое занятие]; [3, примеры 1.11 – 1.15].
