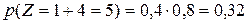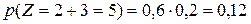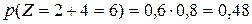Свойство 1.Характеристическая функция определена для любой случайной величины. При этом 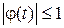 ,
, 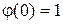 .
.
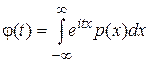 .
.
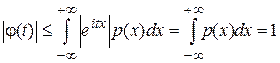 .
.
Поскольку 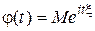 , то
, то 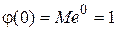
Свойство 2.Характеристическая функция случайной величины 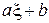 , где a, b—некоторые числа.
, где a, b—некоторые числа.
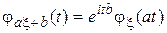 .
.
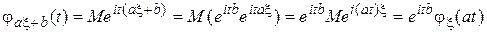 .
.
Если случайные величины
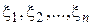
—независимы, то характеристическая функция суммы
§ 5. Геометрические вероятности. Предположим, что на числовой оси имеется некоторый отрезок [a,b] и на этот отрезок наудачу бросается точка. Найти вероятность того, что эта точка попадет на 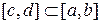 . . 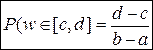 —геометрическая вероятность на прямой. Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания точки в фигуру g определяется равенством: —геометрическая вероятность на прямой. Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания точки в фигуру g определяется равенством: 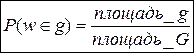 —геометрическая вероятность на плоскости. Пусть в пространстве имеется фигура v, составляющая часть фигуры V. На фигуру V наудачу брошена точка. Вероятность попадания точки в фигуру v определяется равенством: —геометрическая вероятность на плоскости. Пусть в пространстве имеется фигура v, составляющая часть фигуры V. На фигуру V наудачу брошена точка. Вероятность попадания точки в фигуру v определяется равенством: 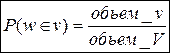 —геометрическая вероятность в пространстве. Недостатком классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным числом исходов. Для устранения этого недостатка и вводят геометрические вероятности. § 6. Свойства вероятности. —геометрическая вероятность в пространстве. Недостатком классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным числом исходов. Для устранения этого недостатка и вводят геометрические вероятности. § 6. Свойства вероятности. | |
| 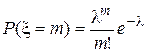 , m=0,1,2,… , m=0,1,2,…
Если 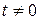 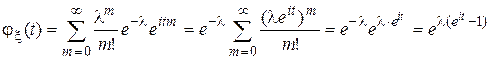 . t=0, . t=0, 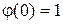 . .
Производящая функция 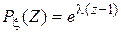 . . Таблица 1. Производящие функции. | Название распределения | Формула для 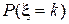 | Производящая функция 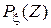 | | Геометрическое | 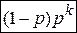 , k=0,1,2,… pqk , k=0,1,2,… pqk | 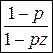 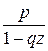 | | Биномиальное | 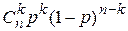 , k=0,1,2…,n. , k=0,1,2…,n. | 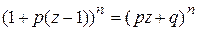 | | Пуассоновское | 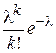 , k=0,1,… , k=0,1,… | 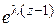 | Таблица 2. Характеристические функции. | Название распределения | Формула для 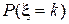 или плотности или плотности | Характеристическая функция 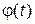 | | Биномиальное | 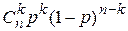 , k=0,1,2… , k=0,1,2… | 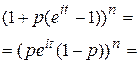 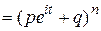 | | Пуассоновское | 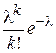 , k=0,1,2,.. , k=0,1,2,.. | 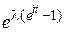 | | | | |
Свойство 1.Вероятность невозможного события равна 0, т.е. 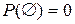 . . 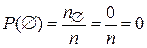 . Свойство 2.Вероятность достоверного события равна 1, т.е. . Свойство 2.Вероятность достоверного события равна 1, т.е. 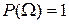 , , 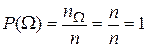 . Свойство 3.Для любого события . Свойство 3.Для любого события 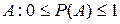 . . 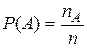 , т.к. , т.к. 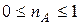 , то , то 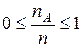 и следовательно и следовательно 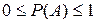 . Свойство 4.Если события А и В несовместимы, то вероятность суммы равна сумме вероятностей: . Свойство 4.Если события А и В несовместимы, то вероятность суммы равна сумме вероятностей: 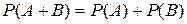 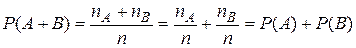 Свойство 5. (обобщенная теорема сложения вероятностей) Свойство 5. (обобщенная теорема сложения вероятностей) 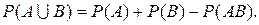 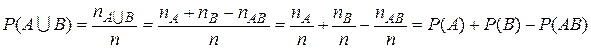 . Свойство 6. (теорема сложения k слагаемых) Если события А1, А2,…, Аk попарно несовместимы, то . Свойство 6. (теорема сложения k слагаемых) Если события А1, А2,…, Аk попарно несовместимы, то 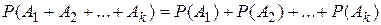 . Свойство 7.Если . Свойство 7.Если 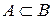 (А влечет В), то (А влечет В), то 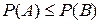 . . 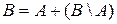 , тогда , тогда | |
| 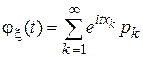 . .
Случай 2. Пусть 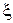 —целочисленная случайная величина с плотностью —целочисленная случайная величина с плотностью 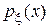 . Тогда характеристическая функция . Тогда характеристическая функция 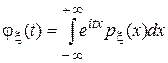 . . Пример 1. Пусть 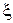 —целочисленная случайная величина с производящей функцией —целочисленная случайная величина с производящей функцией 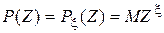 . Тогда характеристическая функция случайной величины . Тогда характеристическая функция случайной величины 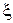 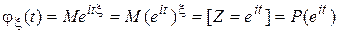 —производящая функция от аргумента —производящая функция от аргумента 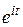 . . Пример 2. Пусть случайная величина 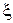 имеет биномиальное распределение с параметрами (n,p), т.е. имеет биномиальное распределение с параметрами (n,p), т.е. 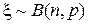 . Найти характеристическую функцию . Найти характеристическую функцию 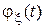 . . 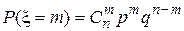 , m=0,1,2…,n. , m=0,1,2…,n. 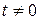 . .
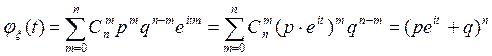 . .
Если t=0, то 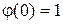 . . Из примера 1, § 12 найдена производящая функция случайной величины 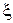 , , 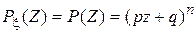 , если , если 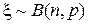 . .
Пример 3. Пусть случайная величина 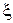 имеет пуассоновское распределение с параметром λ, т.е. имеет пуассоновское распределение с параметром λ, т.е. 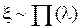 . Найти характеристическую и производящую функции. . Найти характеристическую и производящую функции. | |
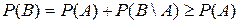 . Свойство 8.Если . Свойство 8.Если 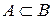 , то , то 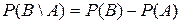 . . 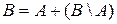 . Следовательно, . Следовательно, 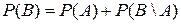 . Тогда . Тогда 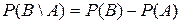 . Свойство 9. . Свойство 9. 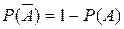 . . 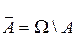 , , 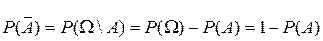 . Свойство 10.Если события Н1, Н2,…,Нk образуют полную группу, то . Свойство 10.Если события Н1, Н2,…,Нk образуют полную группу, то 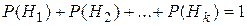 . Т.к. . Т.к. 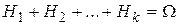 , то по свойству 6: , то по свойству 6: 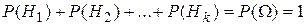 § 7. Условная вероятность. Независимость. o Условной вероятностьюсобытия B при условии A называется вероятность события B в предположении, что событие A наступило. Обозначение § 7. Условная вероятность. Независимость. o Условной вероятностьюсобытия B при условии A называется вероятность события B в предположении, что событие A наступило. Обозначение 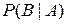 , (реже , (реже 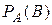 ). ). 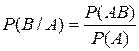 . . 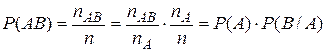 . Теорема (умножение вероятностей): . Теорема (умножение вероятностей): 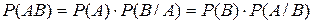 . Теорема (обобщенная теорема умножения). . Теорема (обобщенная теорема умножения). | |
Распределение Фишера F определяется двумя параметрами—числами степеней свободы. § 23. Характеристические функции. 0. 1Случайная величина 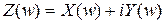 , где i—мнимая единица, т.е. , где i—мнимая единица, т.е. 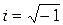 ,а X и Y—действительные случайные величины, называется комплекснозначной случайной величиной. (i2= –1). 0. 2Математическим ожиданием комплекснозначной случайной величины Z называется ,а X и Y—действительные случайные величины, называется комплекснозначной случайной величиной. (i2= –1). 0. 2Математическим ожиданием комплекснозначной случайной величины Z называется 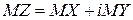 . Все свойства математического ожидания остаются справедливыми для комплекснозначных случайных величин. 0. 3Комплекснозначные случайные величины Z1=X1+iY1 и Z2=X2+iY2 называются независимыми, если независимы соответственно . Все свойства математического ожидания остаются справедливыми для комплекснозначных случайных величин. 0. 3Комплекснозначные случайные величины Z1=X1+iY1 и Z2=X2+iY2 называются независимыми, если независимы соответственно 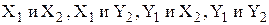 . Свойство комплекснозначных случайных величин. Если комлекснозначные случайные величины Z1 и Z2—независимы, то математическое ожидание их произведения равно произведению математических ожиданий, т.е. . Свойство комплекснозначных случайных величин. Если комлекснозначные случайные величины Z1 и Z2—независимы, то математическое ожидание их произведения равно произведению математических ожиданий, т.е. 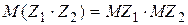 . . 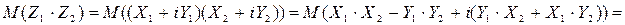 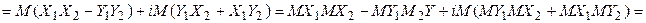 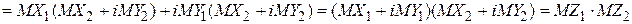 . 0. 4 Характеристической функцией случайной величины . 0. 4 Характеристической функцией случайной величины 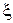 называется функция называется функция 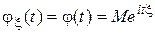 , где , где  . Формулы для вычисления характеристической функции. Случай 1. Пусть . Формулы для вычисления характеристической функции. Случай 1. Пусть 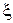 —дискретная случайная величина с рядом распределения —дискретная случайная величина с рядом распределения 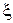 | x1 | x2 | … | | | | |
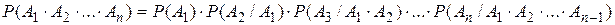 . Доказательство: . Доказательство: 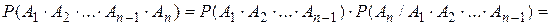 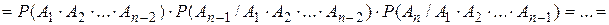 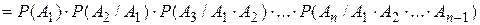 . Пример. Студент знает 20 вопросов из 25, преподаватель задает 3 вопроса. Найти вероятность того, что студент знает все 3 вопроса. А—событие, что студент знает все три вопроса. А1— знает первый вопрос; А2— знает второй вопрос; А3— знает третий вопрос; . Пример. Студент знает 20 вопросов из 25, преподаватель задает 3 вопроса. Найти вероятность того, что студент знает все 3 вопроса. А—событие, что студент знает все три вопроса. А1— знает первый вопрос; А2— знает второй вопрос; А3— знает третий вопрос; 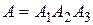 ; ; 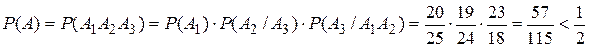 . o События А и В называются независимыми, если . o События А и В называются независимыми, если 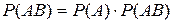 . Свойство. События А и В независимы тогда и только тогда когда P(B/A)=P(B). . Свойство. События А и В независимы тогда и только тогда когда P(B/A)=P(B). 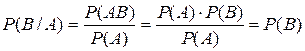 . Пусть P(B/A)=P(B), тогда . Пусть P(B/A)=P(B), тогда 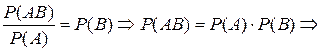 А и В А и В | |
Тогда величина 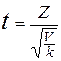 имеет распределение, которое называют t—распределением или распределением Стьюдента (псевдоним английского статистика В.Госсета), с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Плотность распределения случайной величины t имеет вид имеет распределение, которое называют t—распределением или распределением Стьюдента (псевдоним английского статистика В.Госсета), с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Плотность распределения случайной величины t имеет вид 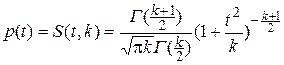 , , 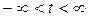 . Случайная величина t имеет математическое ожидание Mt=0, . Случайная величина t имеет математическое ожидание Mt=0, 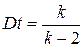 (k>2). § 22. Распределение Фишера. Если U и V—независимые случайные величины, распределенные по закону Х2 со степенями свободы k1 и k2, то величина (k>2). § 22. Распределение Фишера. Если U и V—независимые случайные величины, распределенные по закону Х2 со степенями свободы k1 и k2, то величина 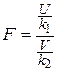 имеет распределение Фишера F со степенями свободы k1 и k2. Плотность этого распределения имеет распределение Фишера F со степенями свободы k1 и k2. Плотность этого распределения 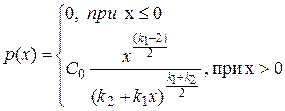 , где , где 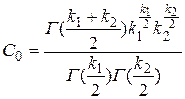 . . | |
независимы. Пример. Бросаются две симметричные монеты. Найти вероятность того, что на обоих монетах выпадут гербы. 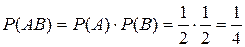 . А–на первой монете герб, В–на второй монете герб. А и В независимы. o События А1,А2,…,Аn называются независимыми (или независимыми в совокупности), если . А–на первой монете герб, В–на второй монете герб. А и В независимы. o События А1,А2,…,Аn называются независимыми (или независимыми в совокупности), если 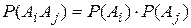 (для i≠j; i,j (для i≠j; i,j 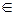 {1,2,3,…,n})–попарная независимость событий; {1,2,3,…,n})–попарная независимость событий; 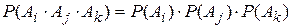 , …, , …, 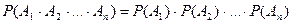 . Можно показать, что из попарной независимости не вытекает независимость в совокупности. § 8. Формулы полной вероятности и Байеса. Теорема 1.Если события Н1, Н2,…,Нn образуют полную группу, то вероятность любого события А можно вычислить по формуле полной вероятности: . Можно показать, что из попарной независимости не вытекает независимость в совокупности. § 8. Формулы полной вероятности и Байеса. Теорема 1.Если события Н1, Н2,…,Нn образуют полную группу, то вероятность любого события А можно вычислить по формуле полной вероятности: 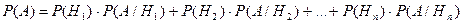 , или , или 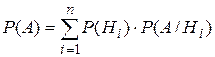 . Так как события образуют полную группу, то можно записать . Так как события образуют полную группу, то можно записать 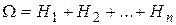 . Событие А может произойти только с одним . Событие А может произойти только с одним | |
§ 20. Распределение «xи квадрат». Пусть Xi, 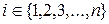 —нормальные независимые случайные величины, причем математическое ожидании каждой из них равно нулю, а среднее квадратическое отклонение (или дисперсия)—единице. Тогда сумма квадратов этих величин —нормальные независимые случайные величины, причем математическое ожидании каждой из них равно нулю, а среднее квадратическое отклонение (или дисперсия)—единице. Тогда сумма квадратов этих величин 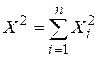 распределена по закону Х2 с k=n степенями свободы. Если же эти величины Хi связаны одним линейным соотношением, например распределена по закону Х2 с k=n степенями свободы. Если же эти величины Хi связаны одним линейным соотношением, например 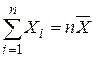 , то число степеней свободы k=n-1. Плотность этого распределения , то число степеней свободы k=n-1. Плотность этого распределения 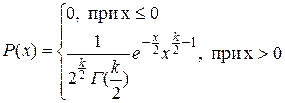 , где , где 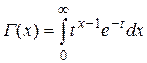 —гамма-функция; в частности, Г(n+1)=n! Отсюда видно, что распределение «x и квадрат» определяется одним параметром—числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному. § 21. Распределение Стьюдента. Пусть Z—нормально распределенная величина, причем M(Z)=0, G2=1, т.е. Z~N(0,1), а V—независимая от Z величина, которая распределена по закону Х2 с k степенями свободы. —гамма-функция; в частности, Г(n+1)=n! Отсюда видно, что распределение «x и квадрат» определяется одним параметром—числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному. § 21. Распределение Стьюдента. Пусть Z—нормально распределенная величина, причем M(Z)=0, G2=1, т.е. Z~N(0,1), а V—независимая от Z величина, которая распределена по закону Х2 с k степенями свободы. | |
из событий Hi, i 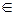 {1,2,…,n}, то А=АН1+АН2+…+АНn. По теореме сложения вероятностей {1,2,…,n}, то А=АН1+АН2+…+АНn. По теореме сложения вероятностей 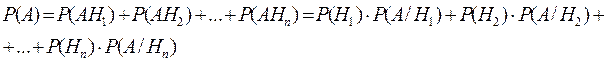 Пример. Имеются 2 урны. В первой—3 белых и 5 черных шаров, во второй—4 белых и три черных. Из первой наудачу взят один шар и переложен во вторую урну. После этого из второй урны был извлечен наудачу шар. Какова вероятность, что он белый? Событие А—из второй урны извлечен шар; Н1—из первой урны во вторую переложен белый шар Н2—из первой урны во вторую переложен черный шар. Пример. Имеются 2 урны. В первой—3 белых и 5 черных шаров, во второй—4 белых и три черных. Из первой наудачу взят один шар и переложен во вторую урну. После этого из второй урны был извлечен наудачу шар. Какова вероятность, что он белый? Событие А—из второй урны извлечен шар; Н1—из первой урны во вторую переложен белый шар Н2—из первой урны во вторую переложен черный шар. 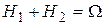 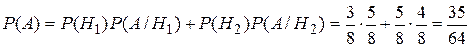 . Замечание: при применении формулы полной вероятности события Н1,Н2,…,Нn , образующие полную группу, называются гипотезами. Теорема 2.Пусть события Н1, Н2, …, Нn образуют полную группу, А–некоторое событие, причем P(A)≠0, тогда имеет место формула Байеса: . Замечание: при применении формулы полной вероятности события Н1,Н2,…,Нn , образующие полную группу, называются гипотезами. Теорема 2.Пусть события Н1, Н2, …, Нn образуют полную группу, А–некоторое событие, причем P(A)≠0, тогда имеет место формула Байеса: 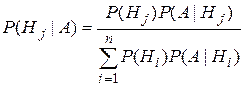 , , 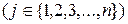 Доказательство: По теореме умножения Доказательство: По теореме умножения | |
| Свойство 6.функция 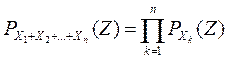 . . 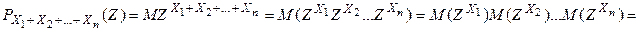 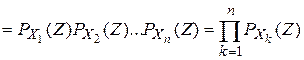 . .
Пример 1. Пусть μ—число успехов в n независимых испытаниях Бернулли, т.е. μ~B(n,p)—биномиальное распределение с параметрами (n,p). Найти производящую функцию случайной величины μ. 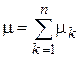 , где μk—число успехов в каждом испытании , где μk—число успехов в каждом испытании
Найдем производящую функцию случайной величины μk 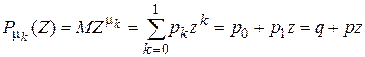 . . 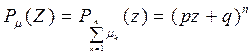 . .
Пример 2. Пусть случайная величина 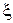 имеет распределение Пуассона с параметром λ, т.е. имеет распределение Пуассона с параметром λ, т.е. 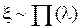 . Найти производящую функцию случайной величины . Найти производящую функцию случайной величины  . . 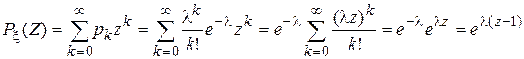 . .
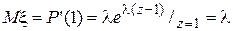 . .
| |
вероятностей 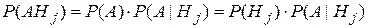 . Отсюда находим вероятность . Отсюда находим вероятность 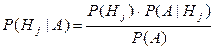 . Остается в знаменателе подставить вместо . Остается в знаменателе подставить вместо 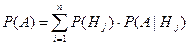 —формула полной вероятности. Пример. Рассмотрим предыдущий пример с учетом того, что из второй урны вынули белый шар. Найти вероятность того, что из первой урны вынули белый шар. Нужно найти P(H1|A). —формула полной вероятности. Пример. Рассмотрим предыдущий пример с учетом того, что из второй урны вынули белый шар. Найти вероятность того, что из первой урны вынули белый шар. Нужно найти P(H1|A). 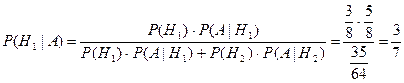 . . 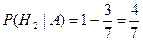 . Замечание. При применении формулы Байеса вероятности . Замечание. При применении формулы Байеса вероятности 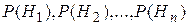 называются априорными вероятностями гипотез. Вероятности P(H1|A),…,P(Hn|A) называют апостериорными вероятностями гипотез. § 9. Схема независимых испытаний Бернулли Полиноминальное распределение. Предположим, что в результате испытания возможны два исхода: «У» и «Н», которые мы называются априорными вероятностями гипотез. Вероятности P(H1|A),…,P(Hn|A) называют апостериорными вероятностями гипотез. § 9. Схема независимых испытаний Бернулли Полиноминальное распределение. Предположим, что в результате испытания возможны два исхода: «У» и «Н», которые мы | |
Свойства производящих функций. Свойство 1.Производящая функция 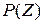 определена в области определена в области 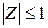 . Свойство 2.Производящая функция . Свойство 2.Производящая функция 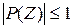 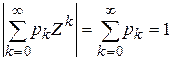 Свойство 3.Значение производящей функции в точке Z=1, P(1)=1. Свойство 3.Значение производящей функции в точке Z=1, P(1)=1. 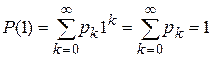 . Свойство 4. Если Z=1, то MX=P’(1) . Свойство 4. Если Z=1, то MX=P’(1) 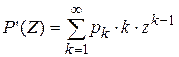 . . 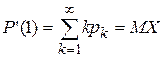 . Свойство 5. . Свойство 5. 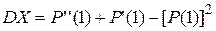 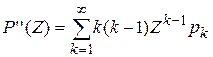 . Если Z=1 . Если Z=1 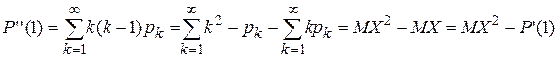 . . 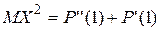 . Следовательно, . Следовательно, 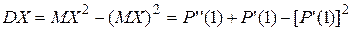 . Если Х1,Х2,…,Хn—независимые целочисленные случайные величины, то производящая . Если Х1,Х2,…,Хn—независимые целочисленные случайные величины, то производящая | |
называем успехом и неудачей. 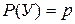 , , 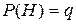 , p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний. o Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию. Элементарным исходом будет являться: (w1,w2,…,wn), , p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний. o Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию. Элементарным исходом будет являться: (w1,w2,…,wn), 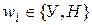 . Всего таких исходов 2n. . Всего таких исходов 2n. 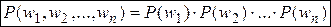 . (1) Формула (1) показывает, что события независимы. Обозначим через µ число успехов в n испытаниях Бернулли. . (1) Формула (1) показывает, что события независимы. Обозначим через µ число успехов в n испытаниях Бернулли. 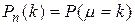 — вероятность того, что в n испытаниях произошло k успехов. Рассмотрим событие — вероятность того, что в n испытаниях произошло k успехов. Рассмотрим событие 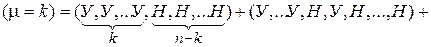 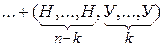 . По теореме сложения получим . По теореме сложения получим 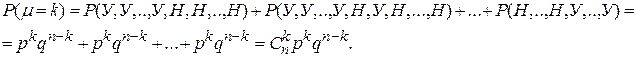 Таким образом, получим Таким образом, получим 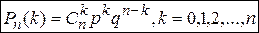 —формула Бернулли. Пример. 2 шахматиста играют в шахматы. —формула Бернулли. Пример. 2 шахматиста играют в шахматы. | |
| 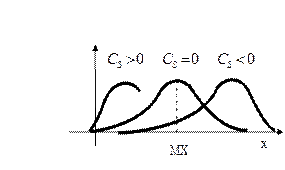 Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию. Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию.
o Эксцессом случайной величины Х называется число 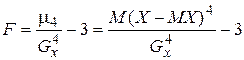 . . Характеризует сглаженность кривой распределения по отношению к кривой нормального распределения. Производящие функции. o Под целочисленной случайной величиной будем понимать дискретную случайную величину, которая может принимать значения 0,1,2,… Таким образом, если случайная величина Х—целочисленная, то она имеет ряд распределения o Пусть Х—целочисленная величина с законом распределения Ее производящей функцией называется функция 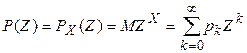 | |
Оба шахматиста равны по силам. Что вероятнее выиграть одну партию из двух или две из четырех (ничьи во внимание не принимаются)? 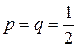 , , 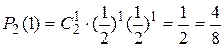 , , 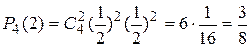 . . 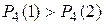 . Полиномиальное распределение. Предположим, что в результате испытания возможны k исходов E1, E2, …, Ek, P(Ei)=pi, . Полиномиальное распределение. Предположим, что в результате испытания возможны k исходов E1, E2, …, Ek, P(Ei)=pi,  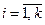 . Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле: . Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле: 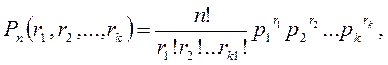 где где 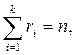 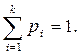 Эта формула полиномиальное распределения, обобщающая формулу Бернулли. § 10 Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа. Теорема. Если вероятность р появления события А в каждом испытании при неограниченном возрастании числа испытаний n Эта формула полиномиальное распределения, обобщающая формулу Бернулли. § 10 Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа. Теорема. Если вероятность р появления события А в каждом испытании при неограниченном возрастании числа испытаний n | |
Свойство 1.корреляции не превосходит единицы, т.е. 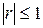 . Свойство 2.Для того чтобы . Свойство 2.Для того чтобы 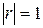 необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е. необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е. 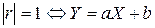 с вероятностью 1. Свойство 3.Если случайные величины независимы, то они некоррелированы, т.е. r=0. Пусть Х и Y—независимы, тогда по свойству математического ожидания с вероятностью 1. Свойство 3.Если случайные величины независимы, то они некоррелированы, т.е. r=0. Пусть Х и Y—независимы, тогда по свойству математического ожидания 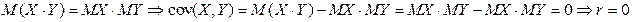 o Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля. o Случайные величины Х и Y называют некоррелированнымиесли их коэффициент корреляции равен 0. Замечание. Из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин. Коэффициент корреляции характеризует тенденцию случайных величин к линейной зависимости. Чем больше по абсолютной величине коэффициент корреляции, тем больше тенденция к линейной зависимости. o Коэффициентом асимметрии случайной величины Х называется число o Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля. o Случайные величины Х и Y называют некоррелированнымиесли их коэффициент корреляции равен 0. Замечание. Из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин. Коэффициент корреляции характеризует тенденцию случайных величин к линейной зависимости. Чем больше по абсолютной величине коэффициент корреляции, тем больше тенденция к линейной зависимости. o Коэффициентом асимметрии случайной величины Х называется число 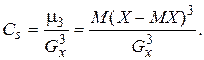 | |
изменяется таким образом, что некоторое событие А появится ровно k раз в n независимых испытаниях стремится к величине 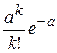 , то есть , то есть 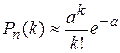 . Доказательство:По формуле Бернулли вероятность того, что событие появится ровно k раз в n независимых испытаниях . Доказательство:По формуле Бернулли вероятность того, что событие появится ровно k раз в n независимых испытаниях 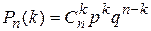 , где q=1-p. Отсюда , где q=1-p. Отсюда 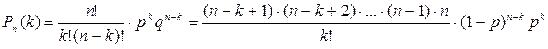 . По условию . По условию 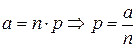 . Подставляя, получим . Подставляя, получим 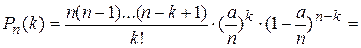 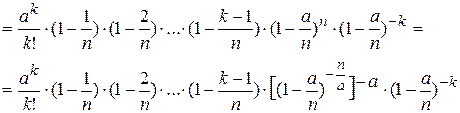 Перейдем к пределу при Перейдем к пределу при 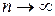 , т.е. , т.е. 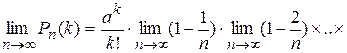 | |
Для описания системы двух случайных величин кроме математических ожиданий и дисперсий используют и другие характеристики. К их числу относятся ковариация и коэффициент коррекции. o Ковариацией между случайными величинами Х и Y называется число 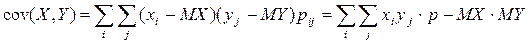 , где , где 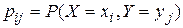 . Для непрерывных случайных величин X и Y используют формулу . Для непрерывных случайных величин X и Y используют формулу 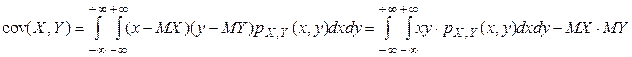 . Покажем, что если случайные величины Х и Y независимы, то . Покажем, что если случайные величины Х и Y независимы, то 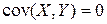 . Пусть Х и Y—непрерывные случайные величины . Пусть Х и Y—непрерывные случайные величины 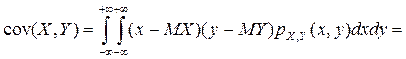 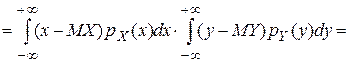 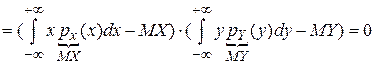 o Коэффициентом корреляции между случайными величинами Х и Y называется число o Коэффициентом корреляции между случайными величинами Х и Y называется число 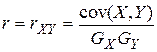 . Свойства корреляции. Абсолютная величина коэффициента . Свойства корреляции. Абсолютная величина коэффициента | |
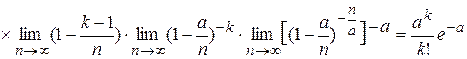 . . 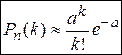 —формула Пуассона. Теоремой удобно пользоваться, когда р→0, —формула Пуассона. Теоремой удобно пользоваться, когда р→0, 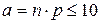 . Существуют специальные таблицы, в которых приведены значения вероятностей для различных а и k. Формулой Бернулли . Существуют специальные таблицы, в которых приведены значения вероятностей для различных а и k. Формулой Бернулли 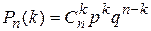 удобно пользоваться, когда значение n не очень велико. Если же n достаточно велико, то удобнее пользоваться приближенными формулами, одна из которых содержится в следующей теореме. Теорема (локальная теорема Муавра-Лапласа). Если вероятность появления события А в каждом отдельном испытании постоянная и отлична от 0 и 1, т.е. 0<p<1, то вероятность того, что событие А появится ровно k раз в n независимых испытаниях. удобно пользоваться, когда значение n не очень велико. Если же n достаточно велико, то удобнее пользоваться приближенными формулами, одна из которых содержится в следующей теореме. Теорема (локальная теорема Муавра-Лапласа). Если вероятность появления события А в каждом отдельном испытании постоянная и отлична от 0 и 1, т.е. 0<p<1, то вероятность того, что событие А появится ровно k раз в n независимых испытаниях. 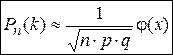 , где , где 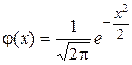 ; ; 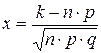 , q=1-p. Без доказательства. Имеются специальные таблицы значений функций φ(х). Нужно учитывать, что функция φ(х)–четная, т.е. φ(х)=φ(-х). Пример. Пусть вероятность появления , q=1-p. Без доказательства. Имеются специальные таблицы значений функций φ(х). Нужно учитывать, что функция φ(х)–четная, т.е. φ(х)=φ(-х). Пример. Пусть вероятность появления | |
В частности, если Х~N(0,1) и Y~N(0,1), то Z=X+Y~N(0,2). Пример 2. Пусть случайная величины Х1,…,Хk—независимы и имеют показательное распределение с параметром λ>0, т.е. 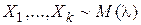 . . 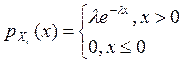 . Найти плотность распределения . Найти плотность распределения 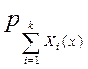 . Если x>0 . Если x>0 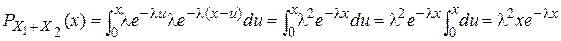 . Если x≤0, то . Если x≤0, то 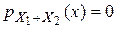 . Таким образом, . Таким образом, 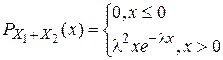 . Далее при x>0 . Далее при x>0 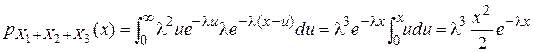 . Если x≤0, то . Если x≤0, то 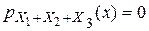 . Проводя аналогичные рассуждения, получим: . Проводя аналогичные рассуждения, получим: 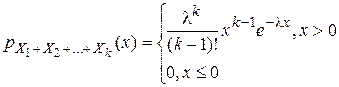 . §18. Числовые характеристики системы двух случайных величин. . §18. Числовые характеристики системы двух случайных величин. | |
события А в каждом отдельном испытании р=0,8. Найти вероятность того. Что событие А появится 75 раз в 100 независимых испытаниях. (k=75, n=100.). По формуле Бернулли 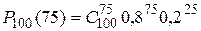 –неудобно. Воспользуемся теоремой Муавра-Лапласа: –неудобно. Воспользуемся теоремой Муавра-Лапласа: 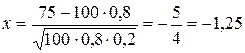 . Значение функции φ(-1,25)=φ(1,25)=0,1826 (по таблице). Тогда искомая вероятность: . Значение функции φ(-1,25)=φ(1,25)=0,1826 (по таблице). Тогда искомая вероятность: 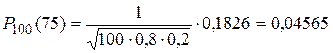 . Теорема (интегральная теорема Муавра-Лапласа). Если вероятность появления события А в каждом отдельном испытании постоянна и отлична от 0 и 1, т.е.0<p<1, то вероятность того, что событие А появится от k1 до k2 раз в n независимых испытаниях определяется выражением: . Теорема (интегральная теорема Муавра-Лапласа). Если вероятность появления события А в каждом отдельном испытании постоянна и отлична от 0 и 1, т.е.0<p<1, то вероятность того, что событие А появится от k1 до k2 раз в n независимых испытаниях определяется выражением: 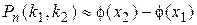 , где , где 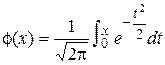 —функция Лапласа, —функция Лапласа, 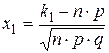 , , 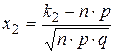 , , 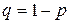 . Без доказательства. Функция Лапласа—нечетная, т.е. . Без доказательства. Функция Лапласа—нечетная, т.е. 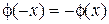 . Значения находят по таблице. Пример. Пусть вероятность появления события А Р(А) в каждом отдельном испытании . Значения находят по таблице. Пример. Пусть вероятность появления события А Р(А) в каждом отдельном испытании | |
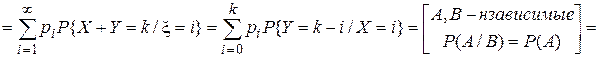 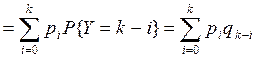 . Таким образом, . Таким образом, 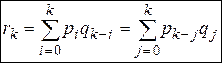 —формула свертки. Случай 2. Пусть Х и Y—непрерывные случайные величины. Теорема.Если Х и Y—независимые непрерывные случайные величины, то случайная величина Z=X+Y—также непрерывна, причем плотность распределения случайной величины Z —формула свертки. Случай 2. Пусть Х и Y—непрерывные случайные величины. Теорема.Если Х и Y—независимые непрерывные случайные величины, то случайная величина Z=X+Y—также непрерывна, причем плотность распределения случайной величины Z 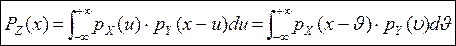 —формула свертки. o Плотность распределения суммы независимых случайных величин называется композицией. Замечание. Если возможные значения X и Y неотрицательны, то формула свертки —формула свертки. o Плотность распределения суммы независимых случайных величин называется композицией. Замечание. Если возможные значения X и Y неотрицательны, то формула свертки 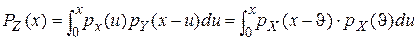 . o Закон распределения вероятностей называется устойчивым, если композиция таких законов есть тот же закон распределения (отличающийся, вообще говоря, параметрами). Нормальный закон обладает свойствами устойчивости, т.е. композиция нормальных законов также имеет нормальное распределение, причем математическое ожидание и дисперсия этой композиции равны соответственно суммам математических ожиданий и дисперсий слагаемых: . o Закон распределения вероятностей называется устойчивым, если композиция таких законов есть тот же закон распределения (отличающийся, вообще говоря, параметрами). Нормальный закон обладает свойствами устойчивости, т.е. композиция нормальных законов также имеет нормальное распределение, причем математическое ожидание и дисперсия этой композиции равны соответственно суммам математических ожиданий и дисперсий слагаемых: 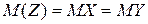 , , 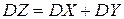 . . | |
| равна 0,8. Найдем вероятность того, что событие А появится более 69 раз в 100 независимых испытаниях. n=100 p=0,8 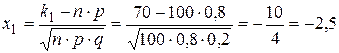 . . q=0,2 k1=70 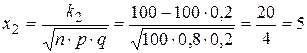 . . k2=100 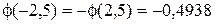 ; ; 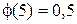
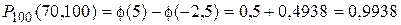 . .
Случайные величины. o Случайной величиной Хназывается функция X(w), отображающая пространство элементарных исходов Ω во множестве действительных чисел R. Пример. Пусть дважды подбрасывается монета. Тогда 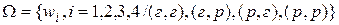 . . Рассмотрим случайную величину Х–число выпадений герба на пространстве элементарных исходов Ω. Множество возможных значений случайной величины:2,1,0. | w | (г,г) | (г,р) | (р,г) | (р,р) | | X(w) | | | | | Множество значений случайной величины обозначается Ωх. Одной из важных характеристик случайной величины является функция распределения случайной величины. Функцией распределения случайной величины Хназывается функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х | |
| значения Х со всеми возможными значениями Х. 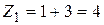 ; ; 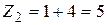 ; ; 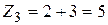 ; ; 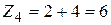 . .
Найдем вероятность этих возможных значений. Для того чтобы Z=4 достаточно, чтобы величина Х приняла значения х1=1 и величина Y—значение y1=3. Вероятности этих возможных значений, как следует из данных законов распределения, соответственно равно 0,4 и 0,2. Поскольку случайные величины Х и Y независимы, то события Х=1 и Y=3 независимы и, следовательно, вероятность их совместного наступления (т.е вероятность события Z=1+3=4) по теореме умножения равна 0,4·0,2=0,08. Аналогично найдем 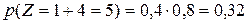
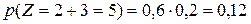
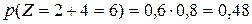
Напишем искомое распределение, сложив предварительно вероятности несовместимых событий Z=z2 и Z=z3. (0,32+0,12=0,44) Контроль: 0,08+0,44+0,48=1. Рассмотрим общий случай: Наши рекомендации | |
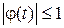 ,
, 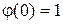 .
.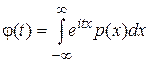 .
.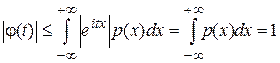 .
.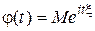 , то
, то 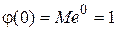
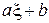 , где a, b—некоторые числа.
, где a, b—некоторые числа.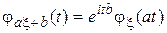 .
.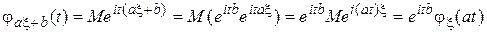 .
.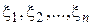 —независимы, то характеристическая функция суммы
—независимы, то характеристическая функция суммы 
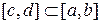 .
. 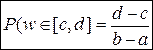 —геометрическая вероятность на прямой. Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания точки в фигуру g определяется равенством:
—геометрическая вероятность на прямой. Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания точки в фигуру g определяется равенством: 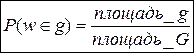 —геометрическая вероятность на плоскости. Пусть в пространстве имеется фигура v, составляющая часть фигуры V. На фигуру V наудачу брошена точка. Вероятность попадания точки в фигуру v определяется равенством:
—геометрическая вероятность на плоскости. Пусть в пространстве имеется фигура v, составляющая часть фигуры V. На фигуру V наудачу брошена точка. Вероятность попадания точки в фигуру v определяется равенством: 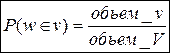 —геометрическая вероятность в пространстве. Недостатком классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным числом исходов. Для устранения этого недостатка и вводят геометрические вероятности. § 6. Свойства вероятности.
—геометрическая вероятность в пространстве. Недостатком классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным числом исходов. Для устранения этого недостатка и вводят геометрические вероятности. § 6. Свойства вероятности. 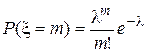 , m=0,1,2,…
, m=0,1,2,…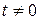
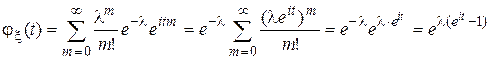 . t=0,
. t=0, 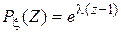 .
.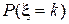
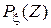
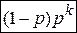 , k=0,1,2,… pqk
, k=0,1,2,… pqk 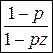
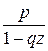
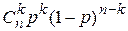 , k=0,1,2…,n.
, k=0,1,2…,n. 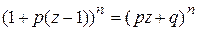
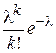 , k=0,1,…
, k=0,1,… 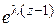
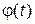
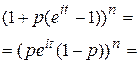
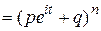
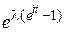
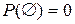 .
. 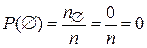 . Свойство 2.Вероятность достоверного события равна 1, т.е.
. Свойство 2.Вероятность достоверного события равна 1, т.е. 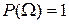 ,
, 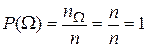 . Свойство 3.Для любого события
. Свойство 3.Для любого события 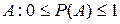 .
. 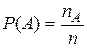 , т.к.
, т.к. 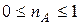 , то
, то 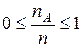 и следовательно
и следовательно 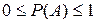 . Свойство 4.Если события А и В несовместимы, то вероятность суммы равна сумме вероятностей:
. Свойство 4.Если события А и В несовместимы, то вероятность суммы равна сумме вероятностей: 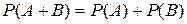
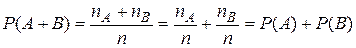 Свойство 5. (обобщенная теорема сложения вероятностей)
Свойство 5. (обобщенная теорема сложения вероятностей) 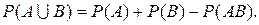
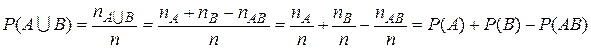 . Свойство 6. (теорема сложения k слагаемых) Если события А1, А2,…, Аk попарно несовместимы, то
. Свойство 6. (теорема сложения k слагаемых) Если события А1, А2,…, Аk попарно несовместимы, то 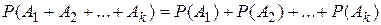 . Свойство 7.Если
. Свойство 7.Если 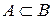 (А влечет В), то
(А влечет В), то 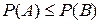 .
. 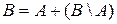 , тогда
, тогда 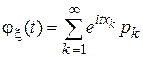 .
.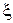 —целочисленная случайная величина с плотностью
—целочисленная случайная величина с плотностью 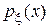 . Тогда характеристическая функция
. Тогда характеристическая функция 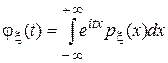 .
.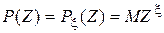 . Тогда характеристическая функция случайной величины
. Тогда характеристическая функция случайной величины 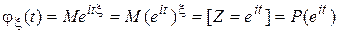 —производящая функция от аргумента
—производящая функция от аргумента 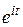 .
.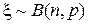 . Найти характеристическую функцию
. Найти характеристическую функцию 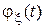 .
. 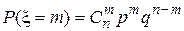 , m=0,1,2…,n.
, m=0,1,2…,n.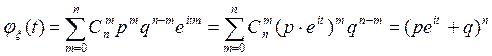 .
.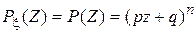 , если
, если 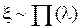 . Найти характеристическую и производящую функции.
. Найти характеристическую и производящую функции.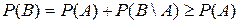 . Свойство 8.Если
. Свойство 8.Если 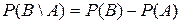 .
. 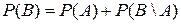 . Тогда
. Тогда 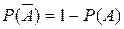 .
. 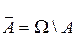 ,
, 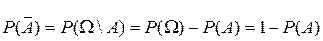 . Свойство 10.Если события Н1, Н2,…,Нk образуют полную группу, то
. Свойство 10.Если события Н1, Н2,…,Нk образуют полную группу, то 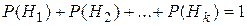 . Т.к.
. Т.к. 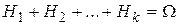 , то по свойству 6:
, то по свойству 6: 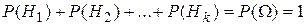 § 7. Условная вероятность. Независимость. o Условной вероятностьюсобытия B при условии A называется вероятность события B в предположении, что событие A наступило. Обозначение
§ 7. Условная вероятность. Независимость. o Условной вероятностьюсобытия B при условии A называется вероятность события B в предположении, что событие A наступило. Обозначение 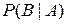 , (реже
, (реже 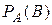 ).
). 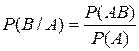 .
. 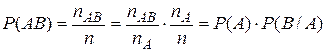 . Теорема (умножение вероятностей):
. Теорема (умножение вероятностей): 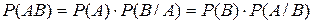 . Теорема (обобщенная теорема умножения).
. Теорема (обобщенная теорема умножения). 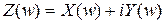 , где i—мнимая единица, т.е.
, где i—мнимая единица, т.е. 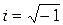 ,а X и Y—действительные случайные величины, называется комплекснозначной случайной величиной. (i2= –1). 0. 2Математическим ожиданием комплекснозначной случайной величины Z называется
,а X и Y—действительные случайные величины, называется комплекснозначной случайной величиной. (i2= –1). 0. 2Математическим ожиданием комплекснозначной случайной величины Z называется 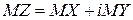 . Все свойства математического ожидания остаются справедливыми для комплекснозначных случайных величин. 0. 3Комплекснозначные случайные величины Z1=X1+iY1 и Z2=X2+iY2 называются независимыми, если независимы соответственно
. Все свойства математического ожидания остаются справедливыми для комплекснозначных случайных величин. 0. 3Комплекснозначные случайные величины Z1=X1+iY1 и Z2=X2+iY2 называются независимыми, если независимы соответственно 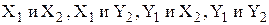 . Свойство комплекснозначных случайных величин. Если комлекснозначные случайные величины Z1 и Z2—независимы, то математическое ожидание их произведения равно произведению математических ожиданий, т.е.
. Свойство комплекснозначных случайных величин. Если комлекснозначные случайные величины Z1 и Z2—независимы, то математическое ожидание их произведения равно произведению математических ожиданий, т.е. 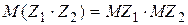 .
. 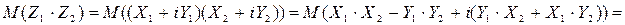
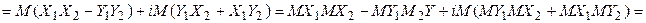
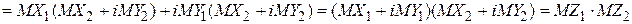 . 0. 4 Характеристической функцией случайной величины
. 0. 4 Характеристической функцией случайной величины 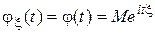 , где
, где  . Формулы для вычисления характеристической функции. Случай 1. Пусть
. Формулы для вычисления характеристической функции. Случай 1. Пусть 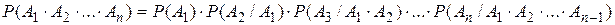 . Доказательство:
. Доказательство: 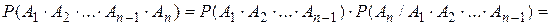
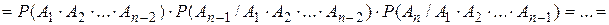
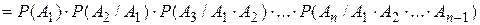 . Пример. Студент знает 20 вопросов из 25, преподаватель задает 3 вопроса. Найти вероятность того, что студент знает все 3 вопроса. А—событие, что студент знает все три вопроса. А1— знает первый вопрос; А2— знает второй вопрос; А3— знает третий вопрос;
. Пример. Студент знает 20 вопросов из 25, преподаватель задает 3 вопроса. Найти вероятность того, что студент знает все 3 вопроса. А—событие, что студент знает все три вопроса. А1— знает первый вопрос; А2— знает второй вопрос; А3— знает третий вопрос; 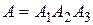 ;
; 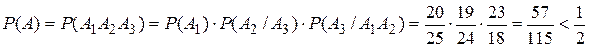 . o События А и В называются независимыми, если
. o События А и В называются независимыми, если 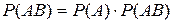 . Свойство. События А и В независимы тогда и только тогда когда P(B/A)=P(B).
. Свойство. События А и В независимы тогда и только тогда когда P(B/A)=P(B). 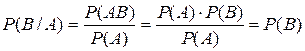 . Пусть P(B/A)=P(B), тогда
. Пусть P(B/A)=P(B), тогда 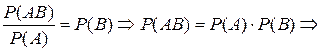 А и В
А и В 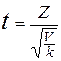 имеет распределение, которое называют t—распределением или распределением Стьюдента (псевдоним английского статистика В.Госсета), с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Плотность распределения случайной величины t имеет вид
имеет распределение, которое называют t—распределением или распределением Стьюдента (псевдоним английского статистика В.Госсета), с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному. Плотность распределения случайной величины t имеет вид 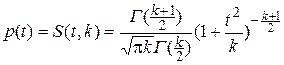 ,
, 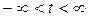 . Случайная величина t имеет математическое ожидание Mt=0,
. Случайная величина t имеет математическое ожидание Mt=0, 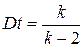 (k>2). § 22. Распределение Фишера. Если U и V—независимые случайные величины, распределенные по закону Х2 со степенями свободы k1 и k2, то величина
(k>2). § 22. Распределение Фишера. Если U и V—независимые случайные величины, распределенные по закону Х2 со степенями свободы k1 и k2, то величина 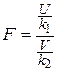 имеет распределение Фишера F со степенями свободы k1 и k2. Плотность этого распределения
имеет распределение Фишера F со степенями свободы k1 и k2. Плотность этого распределения 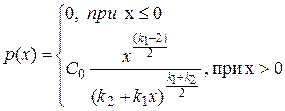 , где
, где 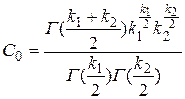 .
. 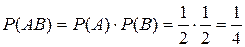 . А–на первой монете герб, В–на второй монете герб. А и В независимы. o События А1,А2,…,Аn называются независимыми (или независимыми в совокупности), если
. А–на первой монете герб, В–на второй монете герб. А и В независимы. o События А1,А2,…,Аn называются независимыми (или независимыми в совокупности), если 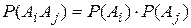 (для i≠j; i,j
(для i≠j; i,j 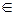 {1,2,3,…,n})–попарная независимость событий;
{1,2,3,…,n})–попарная независимость событий; 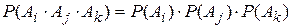 , …,
, …, 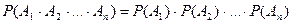 . Можно показать, что из попарной независимости не вытекает независимость в совокупности. § 8. Формулы полной вероятности и Байеса. Теорема 1.Если события Н1, Н2,…,Нn образуют полную группу, то вероятность любого события А можно вычислить по формуле полной вероятности:
. Можно показать, что из попарной независимости не вытекает независимость в совокупности. § 8. Формулы полной вероятности и Байеса. Теорема 1.Если события Н1, Н2,…,Нn образуют полную группу, то вероятность любого события А можно вычислить по формуле полной вероятности: 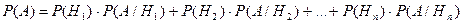 , или
, или 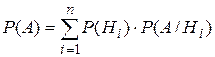 . Так как события образуют полную группу, то можно записать
. Так как события образуют полную группу, то можно записать 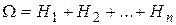 . Событие А может произойти только с одним
. Событие А может произойти только с одним 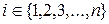 —нормальные независимые случайные величины, причем математическое ожидании каждой из них равно нулю, а среднее квадратическое отклонение (или дисперсия)—единице. Тогда сумма квадратов этих величин
—нормальные независимые случайные величины, причем математическое ожидании каждой из них равно нулю, а среднее квадратическое отклонение (или дисперсия)—единице. Тогда сумма квадратов этих величин 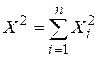 распределена по закону Х2 с k=n степенями свободы. Если же эти величины Хi связаны одним линейным соотношением, например
распределена по закону Х2 с k=n степенями свободы. Если же эти величины Хi связаны одним линейным соотношением, например 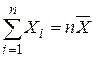 , то число степеней свободы k=n-1. Плотность этого распределения
, то число степеней свободы k=n-1. Плотность этого распределения 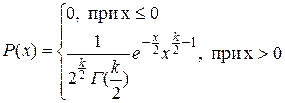 , где
, где 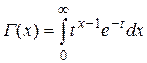 —гамма-функция; в частности, Г(n+1)=n! Отсюда видно, что распределение «x и квадрат» определяется одним параметром—числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному. § 21. Распределение Стьюдента. Пусть Z—нормально распределенная величина, причем M(Z)=0, G2=1, т.е. Z~N(0,1), а V—независимая от Z величина, которая распределена по закону Х2 с k степенями свободы.
—гамма-функция; в частности, Г(n+1)=n! Отсюда видно, что распределение «x и квадрат» определяется одним параметром—числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному. § 21. Распределение Стьюдента. Пусть Z—нормально распределенная величина, причем M(Z)=0, G2=1, т.е. Z~N(0,1), а V—независимая от Z величина, которая распределена по закону Х2 с k степенями свободы. 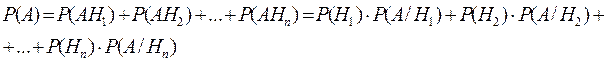 Пример. Имеются 2 урны. В первой—3 белых и 5 черных шаров, во второй—4 белых и три черных. Из первой наудачу взят один шар и переложен во вторую урну. После этого из второй урны был извлечен наудачу шар. Какова вероятность, что он белый? Событие А—из второй урны извлечен шар; Н1—из первой урны во вторую переложен белый шар Н2—из первой урны во вторую переложен черный шар.
Пример. Имеются 2 урны. В первой—3 белых и 5 черных шаров, во второй—4 белых и три черных. Из первой наудачу взят один шар и переложен во вторую урну. После этого из второй урны был извлечен наудачу шар. Какова вероятность, что он белый? Событие А—из второй урны извлечен шар; Н1—из первой урны во вторую переложен белый шар Н2—из первой урны во вторую переложен черный шар. 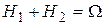
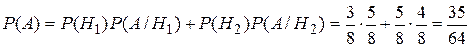 . Замечание: при применении формулы полной вероятности события Н1,Н2,…,Нn , образующие полную группу, называются гипотезами. Теорема 2.Пусть события Н1, Н2, …, Нn образуют полную группу, А–некоторое событие, причем P(A)≠0, тогда имеет место формула Байеса:
. Замечание: при применении формулы полной вероятности события Н1,Н2,…,Нn , образующие полную группу, называются гипотезами. Теорема 2.Пусть события Н1, Н2, …, Нn образуют полную группу, А–некоторое событие, причем P(A)≠0, тогда имеет место формула Байеса: 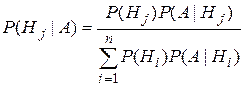 ,
, 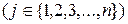 Доказательство: По теореме умножения
Доказательство: По теореме умножения 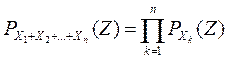 .
.
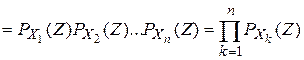 .
.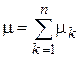 , где μk—число успехов в каждом испытании
, где μk—число успехов в каждом испытании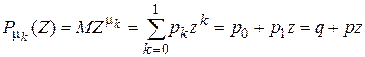 .
.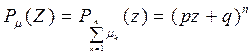 .
.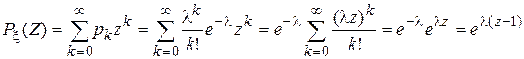 .
.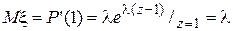 .
.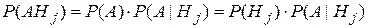 . Отсюда находим вероятность
. Отсюда находим вероятность 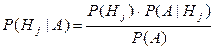 . Остается в знаменателе подставить вместо
. Остается в знаменателе подставить вместо 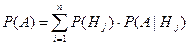 —формула полной вероятности. Пример. Рассмотрим предыдущий пример с учетом того, что из второй урны вынули белый шар. Найти вероятность того, что из первой урны вынули белый шар. Нужно найти P(H1|A).
—формула полной вероятности. Пример. Рассмотрим предыдущий пример с учетом того, что из второй урны вынули белый шар. Найти вероятность того, что из первой урны вынули белый шар. Нужно найти P(H1|A). 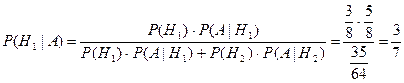 .
. 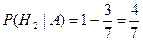 . Замечание. При применении формулы Байеса вероятности
. Замечание. При применении формулы Байеса вероятности 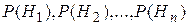 называются априорными вероятностями гипотез. Вероятности P(H1|A),…,P(Hn|A) называют апостериорными вероятностями гипотез. § 9. Схема независимых испытаний Бернулли Полиноминальное распределение. Предположим, что в результате испытания возможны два исхода: «У» и «Н», которые мы
называются априорными вероятностями гипотез. Вероятности P(H1|A),…,P(Hn|A) называют апостериорными вероятностями гипотез. § 9. Схема независимых испытаний Бернулли Полиноминальное распределение. Предположим, что в результате испытания возможны два исхода: «У» и «Н», которые мы 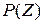 определена в области
определена в области 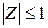 . Свойство 2.Производящая функция
. Свойство 2.Производящая функция 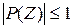
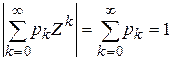 Свойство 3.Значение производящей функции в точке Z=1, P(1)=1.
Свойство 3.Значение производящей функции в точке Z=1, P(1)=1. 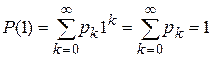 . Свойство 4. Если Z=1, то MX=P’(1)
. Свойство 4. Если Z=1, то MX=P’(1) 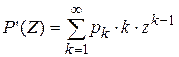 .
. 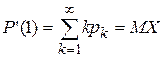 . Свойство 5.
. Свойство 5. 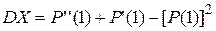
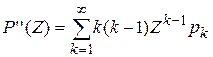 . Если Z=1
. Если Z=1 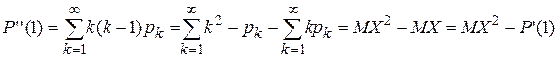 .
. 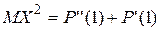 . Следовательно,
. Следовательно, 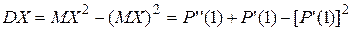 . Если Х1,Х2,…,Хn—независимые целочисленные случайные величины, то производящая
. Если Х1,Х2,…,Хn—независимые целочисленные случайные величины, то производящая 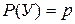 ,
, 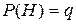 , p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний. o Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию. Элементарным исходом будет являться: (w1,w2,…,wn),
, p+q=1. Предположим, что мы производим независимо друг от друга n таких испытаний. o Последовательность n испытаний называется испытаниями Бернулли, если эти испытания независимы, а в каждом из них возможны два исхода, причем вероятности этих исходов не меняются от испытания к испытанию. Элементарным исходом будет являться: (w1,w2,…,wn), 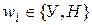 . Всего таких исходов 2n.
. Всего таких исходов 2n. 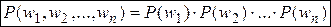 . (1) Формула (1) показывает, что события независимы. Обозначим через µ число успехов в n испытаниях Бернулли.
. (1) Формула (1) показывает, что события независимы. Обозначим через µ число успехов в n испытаниях Бернулли. 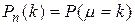 — вероятность того, что в n испытаниях произошло k успехов. Рассмотрим событие
— вероятность того, что в n испытаниях произошло k успехов. Рассмотрим событие 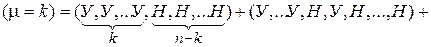
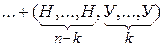 . По теореме сложения получим
. По теореме сложения получим 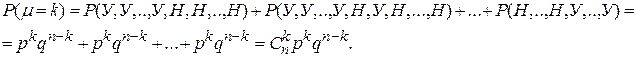 Таким образом, получим
Таким образом, получим 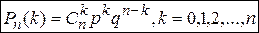 —формула Бернулли. Пример. 2 шахматиста играют в шахматы.
—формула Бернулли. Пример. 2 шахматиста играют в шахматы.  Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию.
Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию.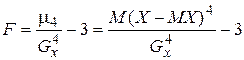 .
.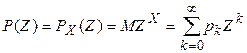
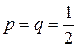 ,
, 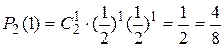 ,
, 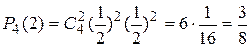 .
. 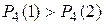 . Полиномиальное распределение. Предположим, что в результате испытания возможны k исходов E1, E2, …, Ek, P(Ei)=pi,
. Полиномиальное распределение. Предположим, что в результате испытания возможны k исходов E1, E2, …, Ek, P(Ei)=pi, 
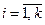 . Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле:
. Тогда вероятность того, что в n независимых испытаниях событие E1 появиться r1 раз, E2 – r2 раз, …, Ek – rk раз вычисляется по формуле: 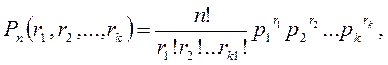 где
где 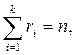
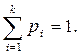 Эта формула полиномиальное распределения, обобщающая формулу Бернулли. § 10 Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа. Теорема. Если вероятность р появления события А в каждом испытании при неограниченном возрастании числа испытаний n
Эта формула полиномиальное распределения, обобщающая формулу Бернулли. § 10 Теорема Пуассона. Локальная и интегральная теоремы Муавра-Лапласа. Теорема. Если вероятность р появления события А в каждом испытании при неограниченном возрастании числа испытаний n 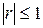 . Свойство 2.Для того чтобы
. Свойство 2.Для того чтобы 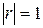 необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е.
необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е. 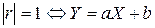 с вероятностью 1. Свойство 3.Если случайные величины независимы, то они некоррелированы, т.е. r=0. Пусть Х и Y—независимы, тогда по свойству математического ожидания
с вероятностью 1. Свойство 3.Если случайные величины независимы, то они некоррелированы, т.е. r=0. Пусть Х и Y—независимы, тогда по свойству математического ожидания 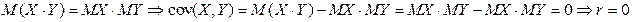 o Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля. o Случайные величины Х и Y называют некоррелированнымиесли их коэффициент корреляции равен 0. Замечание. Из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин. Коэффициент корреляции характеризует тенденцию случайных величин к линейной зависимости. Чем больше по абсолютной величине коэффициент корреляции, тем больше тенденция к линейной зависимости. o Коэффициентом асимметрии случайной величины Х называется число
o Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля. o Случайные величины Х и Y называют некоррелированнымиесли их коэффициент корреляции равен 0. Замечание. Из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин. Коэффициент корреляции характеризует тенденцию случайных величин к линейной зависимости. Чем больше по абсолютной величине коэффициент корреляции, тем больше тенденция к линейной зависимости. o Коэффициентом асимметрии случайной величины Х называется число 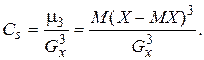
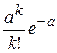 , то есть
, то есть 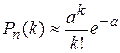 . Доказательство:По формуле Бернулли вероятность того, что событие появится ровно k раз в n независимых испытаниях
. Доказательство:По формуле Бернулли вероятность того, что событие появится ровно k раз в n независимых испытаниях 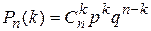 , где q=1-p. Отсюда
, где q=1-p. Отсюда 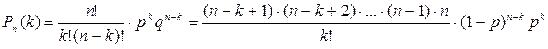 . По условию
. По условию 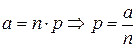 . Подставляя, получим
. Подставляя, получим 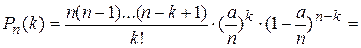
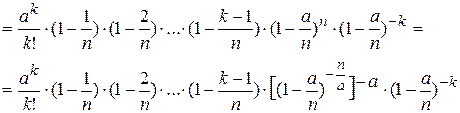 Перейдем к пределу при
Перейдем к пределу при 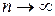 , т.е.
, т.е. 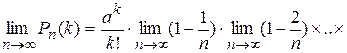
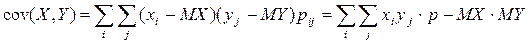 , где
, где 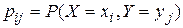 . Для непрерывных случайных величин X и Y используют формулу
. Для непрерывных случайных величин X и Y используют формулу 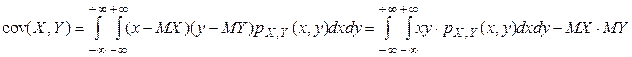 . Покажем, что если случайные величины Х и Y независимы, то
. Покажем, что если случайные величины Х и Y независимы, то 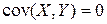 . Пусть Х и Y—непрерывные случайные величины
. Пусть Х и Y—непрерывные случайные величины 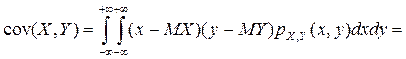
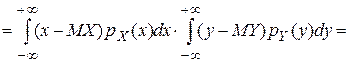
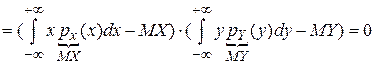 o Коэффициентом корреляции между случайными величинами Х и Y называется число
o Коэффициентом корреляции между случайными величинами Х и Y называется число 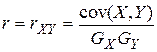 . Свойства корреляции. Абсолютная величина коэффициента
. Свойства корреляции. Абсолютная величина коэффициента 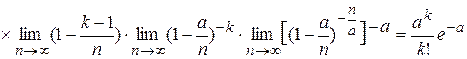 .
. 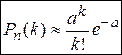 —формула Пуассона. Теоремой удобно пользоваться, когда р→0,
—формула Пуассона. Теоремой удобно пользоваться, когда р→0, 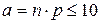 . Существуют специальные таблицы, в которых приведены значения вероятностей для различных а и k. Формулой Бернулли
. Существуют специальные таблицы, в которых приведены значения вероятностей для различных а и k. Формулой Бернулли 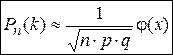 , где
, где 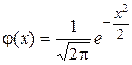 ;
; 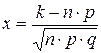 , q=1-p. Без доказательства. Имеются специальные таблицы значений функций φ(х). Нужно учитывать, что функция φ(х)–четная, т.е. φ(х)=φ(-х). Пример. Пусть вероятность появления
, q=1-p. Без доказательства. Имеются специальные таблицы значений функций φ(х). Нужно учитывать, что функция φ(х)–четная, т.е. φ(х)=φ(-х). Пример. Пусть вероятность появления 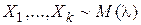 .
. 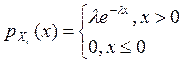 . Найти плотность распределения
. Найти плотность распределения 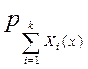 . Если x>0
. Если x>0 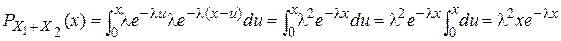 . Если x≤0, то
. Если x≤0, то 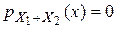 . Таким образом,
. Таким образом, 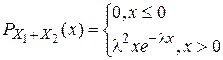 . Далее при x>0
. Далее при x>0 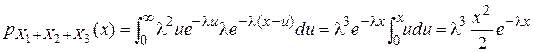 . Если x≤0, то
. Если x≤0, то 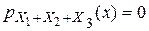 . Проводя аналогичные рассуждения, получим:
. Проводя аналогичные рассуждения, получим: 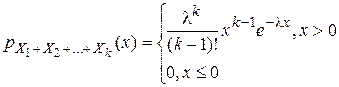 . §18. Числовые характеристики системы двух случайных величин.
. §18. Числовые характеристики системы двух случайных величин. 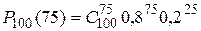 –неудобно. Воспользуемся теоремой Муавра-Лапласа:
–неудобно. Воспользуемся теоремой Муавра-Лапласа: 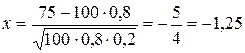 . Значение функции φ(-1,25)=φ(1,25)=0,1826 (по таблице). Тогда искомая вероятность:
. Значение функции φ(-1,25)=φ(1,25)=0,1826 (по таблице). Тогда искомая вероятность: 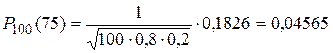 . Теорема (интегральная теорема Муавра-Лапласа). Если вероятность появления события А в каждом отдельном испытании постоянна и отлична от 0 и 1, т.е.0<p<1, то вероятность того, что событие А появится от k1 до k2 раз в n независимых испытаниях определяется выражением:
. Теорема (интегральная теорема Муавра-Лапласа). Если вероятность появления события А в каждом отдельном испытании постоянна и отлична от 0 и 1, т.е.0<p<1, то вероятность того, что событие А появится от k1 до k2 раз в n независимых испытаниях определяется выражением: 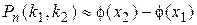 , где
, где 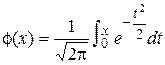 —функция Лапласа,
—функция Лапласа, 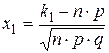 ,
, 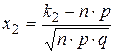 ,
, 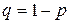 . Без доказательства. Функция Лапласа—нечетная, т.е.
. Без доказательства. Функция Лапласа—нечетная, т.е. 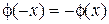 . Значения находят по таблице. Пример. Пусть вероятность появления события А Р(А) в каждом отдельном испытании
. Значения находят по таблице. Пример. Пусть вероятность появления события А Р(А) в каждом отдельном испытании 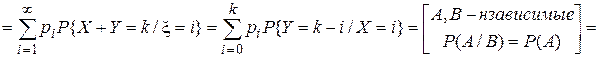
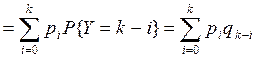 . Таким образом,
. Таким образом, 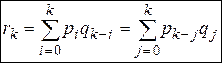 —формула свертки. Случай 2. Пусть Х и Y—непрерывные случайные величины. Теорема.Если Х и Y—независимые непрерывные случайные величины, то случайная величина Z=X+Y—также непрерывна, причем плотность распределения случайной величины Z
—формула свертки. Случай 2. Пусть Х и Y—непрерывные случайные величины. Теорема.Если Х и Y—независимые непрерывные случайные величины, то случайная величина Z=X+Y—также непрерывна, причем плотность распределения случайной величины Z 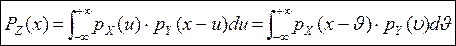 —формула свертки. o Плотность распределения суммы независимых случайных величин называется композицией. Замечание. Если возможные значения X и Y неотрицательны, то формула свертки
—формула свертки. o Плотность распределения суммы независимых случайных величин называется композицией. Замечание. Если возможные значения X и Y неотрицательны, то формула свертки 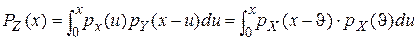 . o Закон распределения вероятностей называется устойчивым, если композиция таких законов есть тот же закон распределения (отличающийся, вообще говоря, параметрами). Нормальный закон обладает свойствами устойчивости, т.е. композиция нормальных законов также имеет нормальное распределение, причем математическое ожидание и дисперсия этой композиции равны соответственно суммам математических ожиданий и дисперсий слагаемых:
. o Закон распределения вероятностей называется устойчивым, если композиция таких законов есть тот же закон распределения (отличающийся, вообще говоря, параметрами). Нормальный закон обладает свойствами устойчивости, т.е. композиция нормальных законов также имеет нормальное распределение, причем математическое ожидание и дисперсия этой композиции равны соответственно суммам математических ожиданий и дисперсий слагаемых: 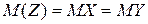 ,
, 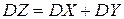 .
. 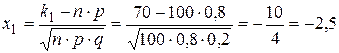 .
.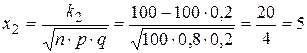 .
.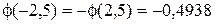 ;
; 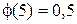
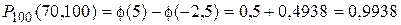 .
.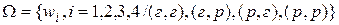 .
.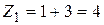 ;
; 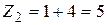 ;
; 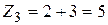 ;
; 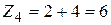 .
.