Свойства операций над множествами
1.  – коммутативность;
– коммутативность;
2.  – ассоциативность;
– ассоциативность;
3. 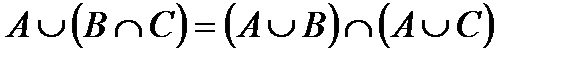 – дистрибутивность;
– дистрибутивность;
4.  – идемпотентность;
– идемпотентность;
5.  – двойное отрицание;
– двойное отрицание;
6. 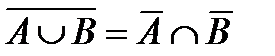 – закон Моргана;
– закон Моргана;
7. 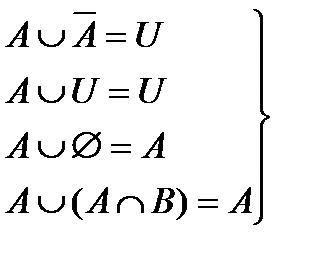 - законы поглощения.
- законы поглощения.
Определение 13.Символы  и
и  , Uи
, Uи  называются двойственными.
называются двойственными.
Методом таблиц Буля легко показать, что имеет место принцип двойственности: при замене в любом свойстве входящих в него символов на двойственные, оно остается верным.
Пример. Докажем, например, закон Моргана.
 | 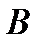 |  |  | 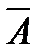 |  |  |
ЭЛЕМЕНТЫ ЛОГИКИ
"Всё наше достоинство заключено в мысли".
Б. Паскаль.
"Но если не грешить против разума, нельзя
вообще ни к чему прийти".
А. Эйнштейн.
Н. Бурбаки начинает свою книгу «Начала математики» так: «Со времён греков говорить «математика» значит говорить «доказательство»». В этом пункте мы обсудим, на чём основано понятие доказательства.
Высказывания
Определение 1. Высказыванием называется любое верифицируемое повествовательное предложение, т.е. предложение, относительно которого можно утверждать истинно оно или ложно.
Пример «  » – высказывание; «сегодня хорошая погода» – не высказывание (для кого как!).
» – высказывание; «сегодня хорошая погода» – не высказывание (для кого как!).
Определение 2.Предложение, содержащее переменную и обращающееся в высказывание при подстановке конкретных значений называют высказывательной формой.
Пример. 
Определение 3.Множество всех возможных истинных интерпретаций высказывания называется смысловым полем (интерпретация – это форма представления информации).
Смысловое поле задано на своём универсуме –множестве всех возможных интерпретаций. Это позволяет высказывания, как и множества, изображать кругами Эйлера. В этом случае характеристическая функция для высказываний имеет вид:

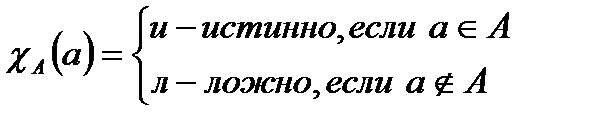 .
.
A –высказывание, а – его интерпретация.
Определение 4. Сложным называется высказывание, составленное из простых с помощью логических операций:ù – неверно, что;  – конъюнкция;
– конъюнкция;  – дизъюнкция;
– дизъюнкция;  – импликация;
– импликация; 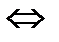 – эквивалентность; и кванторов:
– эквивалентность; и кванторов:  – существует,
– существует,  – для всех,
– для всех,  - тавтология (всегда истинно).
- тавтология (всегда истинно).
Опишем эти операции, используя понятие смыслового поля:

 или ù А – неверно, что А;
или ù А – неверно, что А;

 – дизъюнкция («или»), совокупность (disjunctio – различие);
– дизъюнкция («или»), совокупность (disjunctio – различие);

 – конъюнкция («и»), система (conjunctio – союз);
– конъюнкция («и»), система (conjunctio – союз);

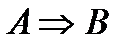 – импликация, теорема (implictio – тесно связывать);
– импликация, теорема (implictio – тесно связывать);

 – эквивалентность (или
– эквивалентность (или 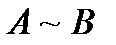 ).
).
Это описание позволяет составить таблицы истинности для этих операций.
| A | B |  |  |  |  |  |
| и | и | л | и | и | и | и |
| и | л | л | и | л | л | л |
| л | и | и | и | л | и | л |
| л | л | и | л | л | и | и |
Теперь можно точно дать определения.
Определение 5 Дизъюнкцией двух высказываний 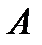 и
и 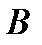 называется новое сложное высказывание
называется новое сложное высказывание  , которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний
, которое истинно тогда и только тогда, когда истинно хотя бы одно из высказываний 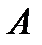 или
или 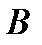 .
.
Определение 6. Конъюнкцией двух высказываний … (самостоятельно)
Определение 7. Эквиваленцией … (самостоятельно).
Определение 8. Импликацией двух высказываний 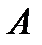 и
и 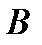 называется новое сложное высказывание
называется новое сложное высказывание  , которое ложно тогда и только тогда, когда высказывание
, которое ложно тогда и только тогда, когда высказывание 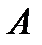 истинно, а высказывание
истинно, а высказывание 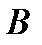 ложно.
ложно.
Импликация  называется ещё теоремой. Тогда говорят, что
называется ещё теоремой. Тогда говорят, что 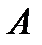 достаточное условие для
достаточное условие для 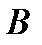 ,
, 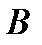 – необходимое условие для
– необходимое условие для 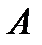 . Теорема
. Теорема  называется прямой,
называется прямой,  – обратной,
– обратной,  – противоположная прямой,
– противоположная прямой,  – противоположная обратной. Используя таблицы истинности, докажем три важных факта:
– противоположная обратной. Используя таблицы истинности, докажем три важных факта:
Теорема 1.Теорема  эквивалентна теореме
эквивалентна теореме  .
.
Теорема 2.Теорема  эквивалентна
эквивалентна  .
.
Теорема 3.Теорема  эквивалентна дизъюнкции
эквивалентна дизъюнкции 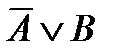 .
.
Доказательство: 
 |  |  |  | 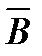 |  | 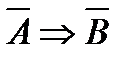 |  |  |
| и | и | и | л | л | и | и | и | и |
| и | л | л | л | и | и | и | л | л |
| л | и | и | и | л | л | л | и | и |
| л | л | и | и | и | и | и | и | и |
■
Теоремы 1 и 2 называют законом контрапозиции, а теорему 3 – дизъюнктивной формой импликации.
Законы логики
Логикой называется наука о способах представления результатов мышления, способах доказательных рассуждений. Любое рассуждение состоит из высказываний. Истинность сложного высказывания, вообще говоря, зависит от истинности элементарных высказываний. Но существует такие сложные высказывания, которые истинны всегда, вне зависимости от истинности элементарных высказываний. Они называются законами логики. Рассмотрим некоторые из них.
I группа –законы, которые нельзя доказать, пользуясь таблицами истинности.
Закон тождества 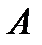 =
= 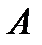 (или
(или 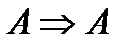 ). Предмет рассмотрения не должен меняться в ходе рассмотрения.
). Предмет рассмотрения не должен меняться в ходе рассмотрения.
Пример.2 и 3 числа. Числа бывают чётные и нечётные. 2 – чётное, 3 –нечётное. Но 2 и 3 есть 5. Следовательно 5 и чётно и нечётно одновременно. (изменился смысл «и»)
Закон достаточного основания. Любое высказывание должно быть достаточно обосновано. Этот закон запрещает ссылки при доказательстве на личное мнение, авторитеты, божественное откровение и пр.
Закон построения отрицания. ù  ~
~ 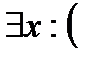 ù
ù  . Неверно, что для любого
. Неверно, что для любого  выполняется условие
выполняется условие  , эквивалентно тому, что существует такой
, эквивалентно тому, что существует такой  , что условие
, что условие  для него не выполняется. Правило построения отрицания для предложений, начинающихся с кванторов заключается в следующем: квантор
для него не выполняется. Правило построения отрицания для предложений, начинающихся с кванторов заключается в следующем: квантор  заменяется на
заменяется на  , квантор
, квантор  заменяется на
заменяется на  , знак отрицания переносится на предложение, стоящее за всеми кванторами.
, знак отрицания переносится на предложение, стоящее за всеми кванторами.
II группа –законы, которые доказываются, используя таблицы истинности. Их формулировка всегда начинается со значка  –«тавтология», т.е. «всегда истинно».
–«тавтология», т.е. «всегда истинно».
Перечислим некоторые из них:
1. Закон исключённого третьего: 

2. Закон исключения противоречий:  ù
ù  .
.
3.Закон двойного отрицания:  ù ù
ù ù  .
.
4. Закон Моргана: 
 ~
~ 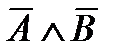 .
.
5. Дизъюнктивная форма импликации: 
 ~
~ 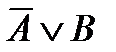 .
.
6. Закон отрицания импликации: 
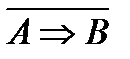 ~
~  .
.
7. Закон транзитивности: 
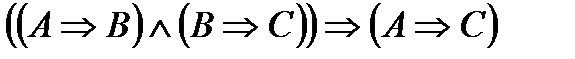 .
.
8. Закон контрапозиции: 
 ~
~  .
.
9. Закон отрицания эквивалентности:  ù
ù 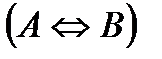 ~
~  .
.
10. Закон образования лжи: 
 .
.
СООТВЕТСТВИЯ
Описания того, что существует хоть в каком – либо
смысле, хоть в каком – либо смысле должны
соответствовать друг другу.
Алекс Алдер.
Соотношения между множествами называются соответствиями. Дляопределения соответствия надо определить два множества: множество (область) определения и множество (область) значений и указать “пары соответствий”. Соотношения между элементами одного множества называются отношениямимежду его элементами.
Определение 1.Два элемента одного или разных множеств, расположенные в определенном порядке, называется упорядоченной парой  .
.
Определение 2.Две упорядоченные пары  и
и 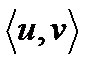 равны, если
равны, если  .
.
Замечание.Естественно,  , если
, если  .
.
Замечание.Упорядоченная n-ка (читается энка):  .
.
Определение 3.Декартовым (прямым) произведением множеств 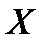 и
и 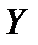 (обозначается
(обозначается 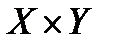 ) называется множество всех упорядоченных пар
) называется множество всех упорядоченных пар  таких, что
таких, что 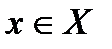 , а
, а  . Множество
. Множество 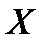 называют областью определения или множеством прообразов, а множество
называют областью определения или множеством прообразов, а множество 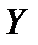 – множеством значений или множеством образов.
– множеством значений или множеством образов.
Определение 4.Любое подмножество декартова произведения 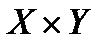 называется бинарным соответствием
называется бинарным соответствием  между множеством
между множеством 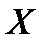 и
и 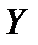 (обозначается
(обозначается 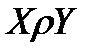 ). Если множества
). Если множества  и
и 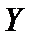 совпадают, то говорят о бинарном отношении.
совпадают, то говорят о бинарном отношении.
Пример. Область определения – студенческая группа, сдающая экзамен; множество значений – отл, хор, уд, неуд – множество оценок. Если явились все, то такое соответствие между студентами и их оценками называется всюду определённым,если кто-то не пришёл, то такое соответствие не всюду определённое.
Определение 5.Соответствие функционально (или является функцией), если каждому элементу области определения соответствует не более одного элемента множества значений.
Пример. Соответствие предыдущего примера функционально, потому что каждому студенту соответствует не более одной оценки. Видно, что функцияможетбытьне всюду определена. Если бы за один экзамен студенты могли получать несколько оценок, то соответствие было быне функционально.
Определение 6.Всюду определённая функция называется отображением, то есть отображение  из
из 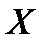 в
в 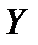 (обозначается
(обозначается  ) – это правило, которое каждому элементу множества
) – это правило, которое каждому элементу множества 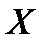 ставит в соответствие единственный элемент множества
ставит в соответствие единственный элемент множества 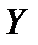 .
.
Комментарий.При этом двум элементам множества 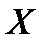 можно ставить в соответствие один и тот же элемент множества
можно ставить в соответствие один и тот же элемент множества 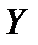 . Отображение всегда функционально. Обратное неверно, то есть не всюду определенная функция не является отображением. Отображение можно записать в виде
. Отображение всегда функционально. Обратное неверно, то есть не всюду определенная функция не является отображением. Отображение можно записать в виде  или
или  , где
, где  и
и 
 элементы некоторых множеств
элементы некоторых множеств 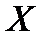 ,
,  , а
, а 
 заданное отображение. Если
заданное отображение. Если 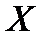 и
и  числа, то
числа, то 
 числовая функция, если
числовая функция, если 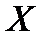 и
и  векторы или функции, то
векторы или функции, то 
 оператор, если
оператор, если 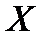
 векторы или функции, а
векторы или функции, а  числа, то
числа, то 
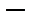 функционал. Иногда понятия отображения и функции не различаются. Тогда отдельно возникает вопрос обобласти определения.
функционал. Иногда понятия отображения и функции не различаются. Тогда отдельно возникает вопрос обобласти определения.
Определение 7. Отображение  называется сюръективным, если
называется сюръективным, если  . Функция
. Функция  называется сюръективной, если каждому
называется сюръективной, если каждому  соответствует, по крайней мере, один
соответствует, по крайней мере, один  .Таким образом, сюръективнымотображением или “отображением НА” или накрытиеммножества
.Таким образом, сюръективнымотображением или “отображением НА” или накрытиеммножества 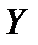 , называют отображение всего множества
, называют отображение всего множества 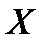 на всё множество
на всё множество 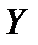 .
.
Пример. Если сопоставить множество студентов в группе с множеством фамилий в списке группы, с учётом возможных однофамильцев, то это отображение и будет сюръекцией, так как каждому студенту соответствует фамилия, но одна и та же фамилия может соответствовать разным студентам.
Определение 7. Отображение или функциональное соответствие называется инъективным, если каждому образу соответствует единственный прообраз, то есть если  . Или, что тоже самое,
. Или, что тоже самое,  . Функция
. Функция  называется инъективной, если каждому
называется инъективной, если каждому  из множества
из множества  соответствует не более одного
соответствует не более одного  .
.
Пример. Если сопоставить множество студентов в группе с множеством фамилий в списке студентов университета и считать, что в группе нет однофамильцев, то такое отображение и называется “отображением В”, или вложением. То есть разным студентам соответствуют разные фамилии, а в области значений могут быть и “незадействованные фамилии”.
Определение 9. Отображение называется биективным, если каждый элемент множества 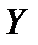 поставлен в соответствие ровно одному элементу множества
поставлен в соответствие ровно одному элементу множества 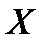 .
.
Комментарий.Соответствие, которое одновременно всюду определено, функционально, инъективно и сюръективно называется биективным.
Определение 10. Биективное отображение множества в себя называется преобразованием.
Определение 12. Отображение называется гомоморфизмом, если: каждому элементу и каждому отношению между элементами множества 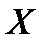 соответствуют один элемент и одно отношение множества
соответствуют один элемент и одно отношение множества 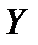 (но необязательно наоборот). Если гомоморфизм биективен, он называется изоморфизм.Изоморфизм
(но необязательно наоборот). Если гомоморфизм биективен, он называется изоморфизм.Изоморфизм  это отображение, сохраняющее порядок, например:
это отображение, сохраняющее порядок, например: 
Определение 13. Гомеоморфизмом называют частный случай изоморфизма. Два множества гомеоморфны, если существует взаимно однозначное и взаимно непрерывное отображение одного из них на другое.
ОТНОШЕНИЯ
Не относитесь к себе слишком всерьёз.
Пятое правило Черчилля.
(первых четырёх не существует)
Комментарий.Соотношения между элементами одного и того же множества называются отношениями. Отношения характеризуются иным перечнем свойств, нежели соответствия.
Определение 1. На некотором множестве  задано отношение
задано отношение 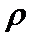 , если для любых двух элементов
, если для любых двух элементов 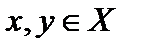 можно сказать, находятся ли они в отношении
можно сказать, находятся ли они в отношении 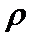 или нет.
или нет.
Комментарий.Можно сказать, что отношение 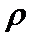 есть отображение
есть отображение 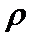 :
:  , где значение 1 соответствует «истине», а значение 0 — «лжи» (здесь важен порядок, в котором берутся элементы
, где значение 1 соответствует «истине», а значение 0 — «лжи» (здесь важен порядок, в котором берутся элементы  и
и  ).
).
Определение 2. Отношение рефлексивно, если 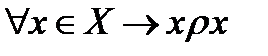 .
.
Комментарий.То есть отношение применимо к самому объекту. Например, отношение включения. Поскольку любое множество включено само в себя, то отношение включения обладает свойством рефлексивности. Отношение «спасения» на множестве утопающих – рефлексивно.
Определение 3. Отношение антирефлексивно, если к самому объекту оно всегда неприменимо.
Например, «перпендикулярность» на множестве прямых. Прямая не может быть перпендикулярна самой себе.
Определение 4. Отношение симметрично, если  .
.
Если Иванов «учится в одной группе» с Петровым, то справедливо и обратное.
Определение 5. Отношение асимметрично, если  , но неверно, что
, но неверно, что  . Если стольник можно “разменять” десятками, то обратное сложно. Определение 6. Отношение антисимметрично, если из
. Если стольник можно “разменять” десятками, то обратное сложно. Определение 6. Отношение антисимметрично, если из 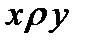 и
и  следует, что
следует, что 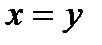 .
.
Определение 7. Полнота отношения означает, что для любой пары разных элементов данного множества данное отношение выполнимо на всём множестве.
Например, отношение “больше или равно” полно на множестве действительных чисел и не полно на множестве комплексных.
Определение 8. Отношение транзитивно, если из  и
и  следует, что
следует, что 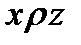 .
.
Комментарий.Если Иванов “учится в одной группе” с Петровым, а Петров с Сидоровым, то Иванов “учится в одной группе” с Сидоровым. Отношение включения тоже транзитивно. Если группа «включена» в множество студентов университета, а это множество «включено» в множество студентов страны, то множество студентов группы «включено» в множество студентов страны. Но если студенческую группу рассматривать как элемент университета, понимаемого как множества, состоящего из групп, а университет рассматривать как элемент высшей школы – множества, состоящего из университетов, то группа не является элементом высшей школы (там элементы университеты). То есть отношение “принадлежности” не транзитивно.
Комментарий.Каждое конкретное отношение обладает совокупностью свойств. Рассмотрим важнейшие группы отношений, у которых совокупности свойств одинаковые.
