Задача 1.2.Корреляционно – Регрессионный анализ
Указания к выполнению работы
Задача № 1: Показатели и прогноз в рядах динамики.
Проанализируйте динамику показателя за указанный период. Для этого вычислите цепные показатели динамики, и средние к ним, постройте график, сделайте выводы о наличии тенденции. Постройте прогноз на следующий период (используя указанный в задании метод прогнозирование).
Задача № 2: Корреляционно – Регрессионный анализ.
Проведите корреляционный анализ факторным и результативным признаками,
если связь линейная вычислите линейный коэффициент корреляции, если нелинейная, эмпирическое корреляционное отношение. Сделайте выводы о силе, направлении и виде связи.
Проведите регрессионный анализ, для этого постройте две модели зависимости (указанные в задании), рассчитайте среднюю ошибку аппроксимации этих моделей. Сделайте выводы.
(Оценку статистической значимости проводить не надо).
1. Степенная модель: линейная y= a0+a1·x, параболическая y= a0+a1·x+a2·x2; кубическая y=a0+a1·x+a2·x2+a3·x3;
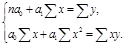
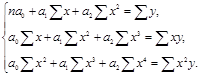
2. Гиперболическая модель: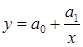 
; 
;
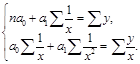3. Показательная модель: 
; Проводят ее линеаризацию с помощью операции логарифмирования: Y=A0 + A1∙x∙, где Y = ln y, A0= ln a0, A1 = ln a1.
Решают систему уравнений 
4. Экспоненциальная модель: 
; Проводят ее линеаризацию с помощью операции логарифмирования: Y=A0 + a1∙x ∙, где Y = ln y, A0= ln a0. 
;
5. Логарифмическая модель: 
, 
.
Задача № 3: Индексный и факторный анализ.
Проведите индексный и факторный анализ показателей, (цены, объемов, товарооборота), для этого рассчитайте
1) сводные индексы: физического объема, цены и товарооборота; изменение товарооборота
2) экономию (перерасход) товарооборота за счет изменения: цен, объемов продаж.
Сделайте выводы.
Проанализируйте изменение средней цены в целом и под влиянием факторов, для этого рассчитайте
3) индексы: переменного состава, фиксированного состава, структурных сдвигов.
Сделайте выводы.
В случае если по исходным данным нельзя рассчитать индексы в агрегатном виде,
рассчитываем их по формулам средних индексов.
Среднеарифметического или Среднегармонического
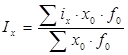
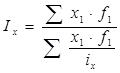
В решении обязательно указываем название индекса, который применяли для вычислений.
Вариант 1
Задача 1.1 Показатели и прогноз в рядах динамики:
| Период | Оборот, тыс. руб. |
| Декабрь2015 | 402,29 |
| Январь 2016 | 373,52 |
| Февраль 2016 | 335,59 |
| Март 2016 | 281,50 |
| Апрель 2016 | 236,13 |
| Май 2016 | 162,31 |
| Июнь 2016 | 189,77 |
| Июль 2016 | 159,32 |
| Август 2016 | 124,37 |
| Сентябрь 2016 | 200,86 |
| Октябрь 2016 | 232,71 |
| Ноябрь 2016 | 248,32 |
| Декабрь 2016 | 234,47 |
Проанализируйте изменение оборота в течение 2006 года (по полугодиям и за год в целом) для этого постройте график, вычислите цепные показатели динамики, и средние показатели за каждое полугодие, сделайте выводы. Постройте прогноз на январь 2017 (используя прогноз по среднему коэффициенту роста).
Задача 1.2.Корреляционно – Регрессионный анализ
| Магазин, № п/п | Оборот, тыс. руб. | Средняя выработка одного работника, тыс. руб. |
| 376,74 | 26,3 | |
| 715,56 | 15,6 | |
| 30,05 | 41,0 | |
| 245,64 | 27,0 | |
| 1010,38 | 13,6 | |
| 259,27 | 21,6 | |
| 583,54 | 20,4 | |
| 225,32 | 28,7 | |
| 908,88 | 14,7 | |
| 277,83 | 22,0 |
Проведите корреляционный анализ (определите наличие, силу и направление связи) между оборотом, тыс. руб. (результативный признак Y) и средней выработкой одного работника, тыс. руб. (факторный признак X), если связь линейная вычислите линейный коэффициент корреляции, если нелинейная, эмпирическое корреляционное отношение. Постройте две модели логарифмическую и параболическую, рассчитайте среднюю ошибку аппроксимации. (Оценку статистической значимости проводить не надо). Сделайте выводы.