Смешанное произведение трех векторов
Смешанным произведением трех векторов а,b,с называется число, которое обозначается символом ахb-с (смешанное произведение иногда называют векторно-скалярным).
Если векторы а,b,с некомпланарны, то смешанное произведение а´b-с равно объему параллелепипеда, построенного на векторах а,b,с, взятому со знаком "+", если упорядоченная тройка векторов а,b,с-правая, и со знаком "-", если эта тройка - левая.
Из свойств смешанного произведения трех векторов следует отметить следующие:
1)при круговой перестановке векторов смешанное произведение не меняется, т.е. (aх b)× с = (сха)× b = (bхс)× а;
2)если в смешанном произведении поменять местами два соседних сомножителя, то произведение изменит знак, т.е. (aх b)× с = -(ахс)× b ;
3) смешанное произведение равно нулю тогда и только тогда, когда векторы компланарны, т.е. условием компланарности векторов является равенство нулю смешанного произведения этих векторов.
Смешанное произведение векторов в декартовом базисе
{i,j,k}.Если а(ax, ay, az), b(bx, by, bz,) и с(сx, cy, cz), то

Условие компланарности векторов 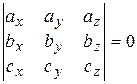 (1.2.12)
(1.2.12)
Наиболее распространенные задачи, решаемые при помощи смешанного произведения:
1)найти объем параллелепипеда, построенного на векторах а,b,с:
V = |а х b× с|,
2) найти объем тетраэдра, построенного на векторах а,b,с:
V=1/6 (|а х b× с|)
3) проверить компланарны ли векторы а,b,с, если а х b× с=0, то векторы компланарны, если а х b× с¹ 0, то векторы некомпланарны;
4)проверить правую или левую тройку образуют векторы а,b,с,
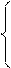 >0 -тройка векторов - правая ,
>0 -тройка векторов - правая ,
а х b× с=.
<0 - тройка векторов левая.
Замечание: смешанное произведение векторов а,b,с, как правило, записывают в виде а× b× с .
Пример 1.2.10. Вычислить длину высоты тетраэдра ABCD, проведенную из вершины D к основанию АВС, если вершины тетраэдра имеют координаты:
А (1,2,0), B(2,1,1), С(0,-3,-1), D(3,3,4). Найдем координаты векторов, выходящих из вершины А:
АВ(1,-1,1), AC(-1,-5,-1), AD(2,1,4), Vтетр=1/6(|АВ×АС×AD|); Vтетр=1/3(SDABC×HD);
SDABC=1/2 (|AB´AC|); HD= 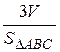 . Отсюда
. Отсюда
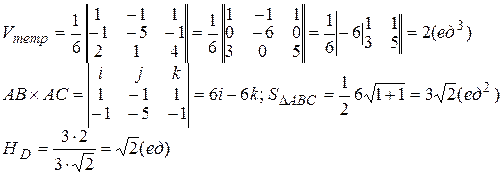
Вопросы для самопроверки:
1.Сформулируйте правила треугольника и параллелограма сложения векторов.
2.Укажите принципиальное различие в формулах для вычисления длины
вектора в произвольном и декартовом базисах.
З. Чему равно скалярное произведение базисных векторов в декартовом
базисе?
4.Чему равно векторное произведение базисных векторов в декартовом
базисе?
5.Запишите условие компланарности векторов. Приведите пример.
6.Можно ли построить треугольник на векторах а,b,а+b ?
7.Приведите пример условия, при выполнении которого из трех векторов a, b,с можно образовать треугольник.
8. Докажите, что объем тетраэдра вычисляется по формуле V= 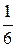 | а× b× с|
| а× b× с|
9. Вычислите угол между векторами, совпадающими со скрещивающимися ребрами тетраэдра.
10.Как Вы считаете, произведение векторов axbxc (двойное векторное) является векторной величиной или скалярной?
