Графоаналитический метод определения кинематических параметров

Графические методы кинематического исследования механизмов обладают наглядностью, удобством контроля.

Графоаналитический метод определения кинематических параметров механизмов сводится к построению планов их положений, скоростей и ускорений.

Определение положений

План положений механизма – это графическое изображение взаимного расположения звеньев, соответствующее выбранному расчетному положению начального звена.

План положений механизма для угла 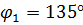показан на рис 2.1. Масштабный коэффициент плана положений 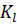определяется как

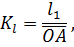
где 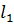- действительная длина звена 1;

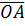– длина отрезка, изображающего звено 1 на плане положений. Тогда отрезок 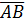, соответствующий длине звена 2, будет

Из плана положений определяется угол 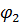и координаты точек B и :

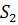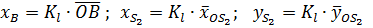
Для рассматриваемого примера численные значения приведенных параметров будут следующие:

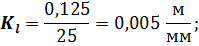
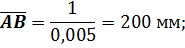
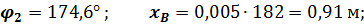
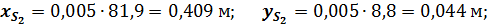
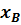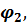
Значения , 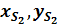с большой степенью точности приближены к значениям, полученным аналитическим способом.

Определение скоростей

Метод основан на графическом решении векторных уравнений движения. Для построения плана скорости должна быть известна кинематическая схема механизма, построенная в масштабе (рис.2.2,а) и задан закон движения начального звена (у нас ).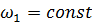

Требуется найти линейные скорости точек A, B и 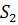, а также угловую скорость звена 2.

Построение плана скоростей начну с определения скорости точки А кривошипа

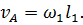
Вектор скорости точки А направлен перпендикулярно кривошипу ОА в направлении его вращения.

10

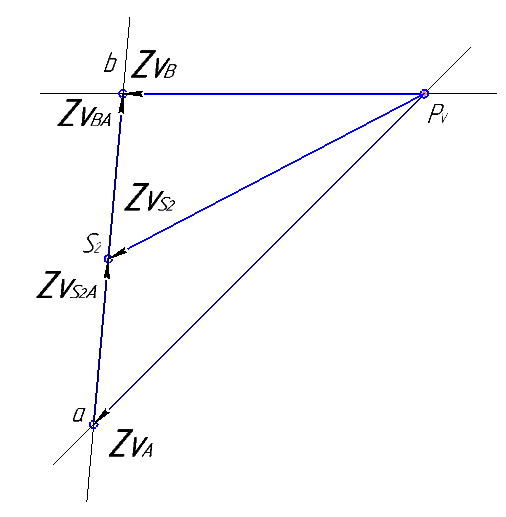
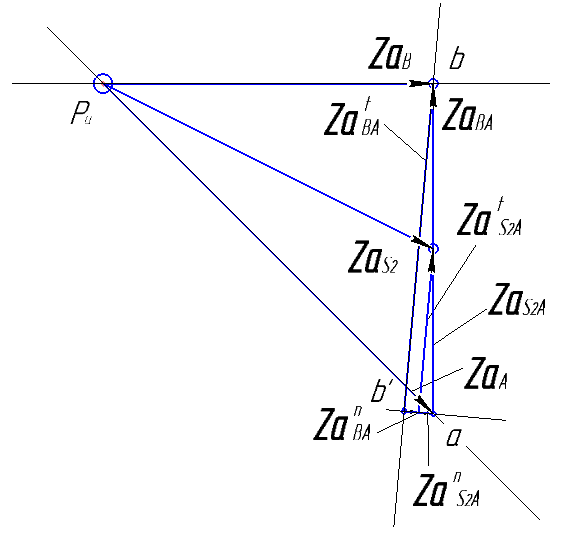
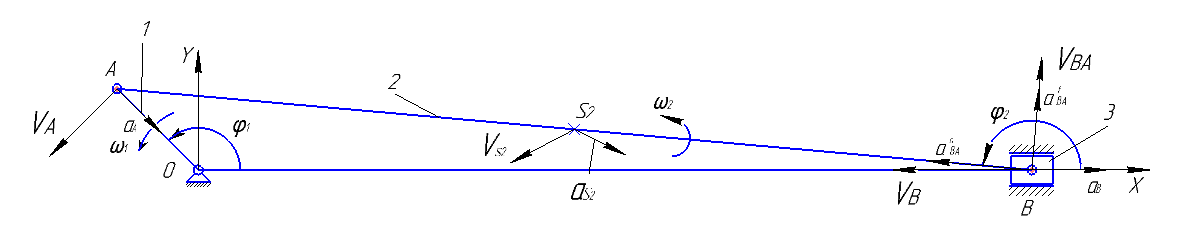
Рис.2.2 Схема механизма, план скоростей и ускорения

Скорость точки В, принадлежащей звену 2, можно представить как векторную сумму скоростей переносного и относительного движений:

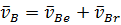
Переносным движением звена 2 является поступательное движение его со скоростью точки А

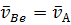
а относительное – вращательное движение звена 2 вокруг точки А. Если обозначить отностиленую скорость через 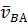, то

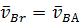
Окончательно векторное уравнение для скорости точки В будет иметь вид

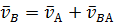
В этом уравнении векторы скорости, известные по величине и направлению, подчеркнуты двумя чертами, а известные лишь по направлению – одной чертой.

Для определения указанных неизвестных величин строию план скорости с выбранным масштабным коэффициентом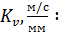

Здесь 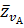– длина отрезка, изображающего на плане скорость 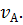11

Из произвольного полюса 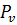(рис.2.2,б) провожу вектор 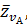перпендикулярный кривошипу ОА, соответствующий на плане скоростей абсолютной скорости 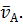Из конца вектора 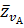(точка а) провожу линию в нарпавлении отрносительной скорости 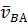, перпендикулярную АВ, а из полюса 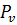– линию в направлении скорости 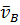, параллельную ОВ. В пересечении указанных линий нахожу точку b. Вектор 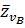изображает скорость 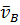точки В, а вектор 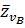– скорость 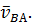Величины действительных скоростей определяю по формулам

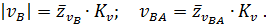
Направление скорости 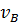определяю при параллельном переносе вектора 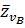в точку В механизма (рис.2.2.а)

Величина угловой скорости звена 2 будет

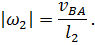
Направление 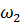нахожу по вектору 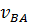(рис.2.2.а)

Скорость точки 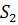определяю с помощью векторного уравнения:

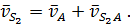
Здесь скорость отностительно движения точки 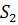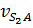находится методом пропорционального деления отрезка ab , изображающего относительную скорость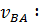

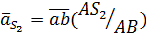
Действительная скорость 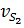определяется как

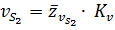
Для рассматриваемого примера численное значение скорости равно

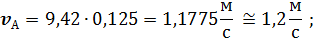
Если на плане скоростей (рис.2.2,б) известную скорость 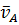изобразить отрезком длинной 100 мм, то получаю:

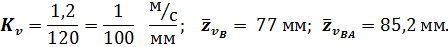
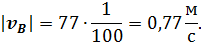
Так как вектор 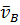в точке В механизма направлен в сторону отрицательной полуоси x, занк скорости будет отрицательным:

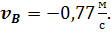
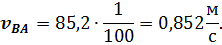
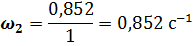
Угловая скорость 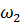направлена против часовой стрелки, поэтому имеет знак «плюс»:

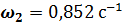
Сравнение с результатами аналитического метода расчета дает ошибку не более 3%.

Определение ускорений

Построение плана ускорений позволяет определить линейные ускорения точек А, В и 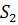, а также угловое ускорение звена 2.

Ускорение точки А кривошипа складывается из суммы нормальной 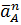и тангенциальной 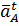составляющих

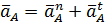
где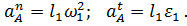

Ускорение точки В здесь представляется в виде векторной суммы ускорений переносного и относительного движений:

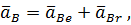
где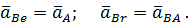

Относительное ускорение точки В также состоит из двух составляющих

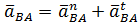
где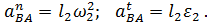

Причем нормальные составляющие ускорений всегода направлены по радиусу к центру вращения, а тангенциальные составляющие перпендикулярны радиусу и направлены в сторону углового ускорения.

С учетом приведенных выше формул и окончательно получим

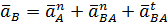
Как и раньше, однй чертой подчеркнуты векторы, известные только по направлению, а полностью известные векторы подчеркнуты двумя чертами.

Построение плана ускорений начинаю с выбора масштабного коэффициента плана ускорений 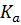по ллюбой известной величине: либо по 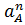, либо по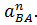

Пусть ,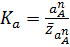

Где 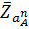– длина отрезка, изображающего ускорение .

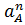Тогда величина отрезка 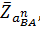изображающего известное ускорение 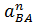, будет

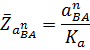
Из произвольной точки полюса плана ускорений (рис.2.2,в) откладываем отрезок 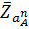в направлении к центру вращения звена 1 – точке 0. Так как 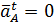, и следовательно, 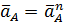, отрезок 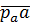изображает полное ускорение точки А.

Из конца отрезка 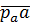параллельно ВА по направлению к центру относительного вращения звена 2 (т.А) откладываем отрезок 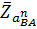и из его конца перпендикулярно к АВ – линию действия тангенциальной составляющей отнсительного ускорения 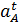. Затем из полюса параллельно ОВ проводим линию действия абсолютного ускорения точки В. Точка b, полученная на пересечении, определяет концы отрезков 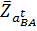и 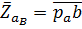, изображающих соответствующие

ускорения.

Величины этих ускорений будут

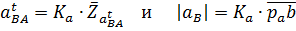
Соединив прямой точки a и b плана ускорений, получим отрезок 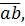изображающий полное относительное ускорение 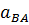. Его величина будет

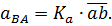
Величина углового ускорения звена 2 определяется из уравнения

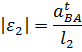
Пернеся вектор ускорения 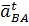в точку В механизма и рассматривая движение точки В относительно точки А, находим направление ускорения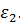

Ускорение точки 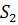определяется из векторного уравнения

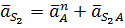
Величина относительного ускорения 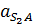находится аналогично скорости 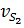- методом пропорционального деления отрезка ab, изображающего относительное ускорение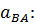

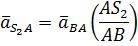
или на рис.2.2,в

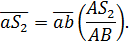
Полное ускорение точки 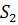определится как

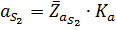
Для рассматриваемого примера расчеты дают следующие значения параметров:

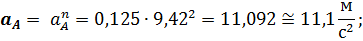
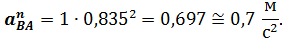
Возьмём отрезок тогда масштабный коэффициент будет равен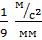

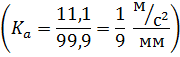
Отрезок, изображающий известное ускорение :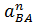

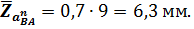
Искомое ускорения будут

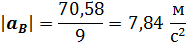
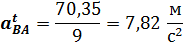
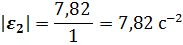
Так как вектор ускорения 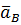направлен в сторону положительной полуоси x, то

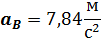
Угловое ускорение 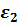направлено против часовой стрелке, поэтому

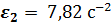
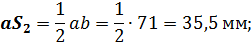
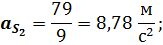
Сравнение результатов расчета со значениями, полученными аналитическим методом, дает максимальную ошибку не более 3%.