Решение системы линейных уравнений
С помощью обратной матрицы
Рассмотрим систему линейных уравнений, представленную матричным уравнением:
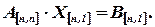
Обе части уравнения умножим слева на обратную матрицу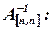 
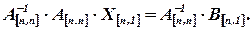
Поскольку
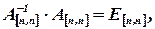
где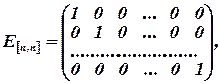 
а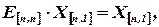 
следовательно,
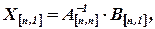
т.е. найдено решение системы линейных уравнений.
Итак, для решения системы линейных уравнений с помощью обратной матрицы необходимо, чтобы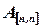 
была квадратной и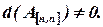 
▼
Примеры
1) Используя обратную матрицу, решить систему линейных уравнений, представленную расширенной матрицей:
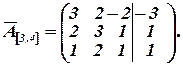
Решение.
= 
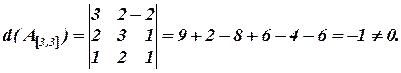
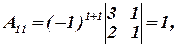
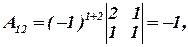
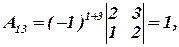
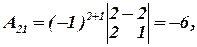
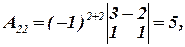
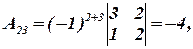
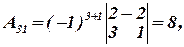
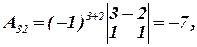
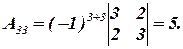
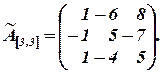
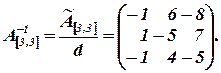
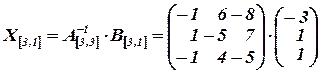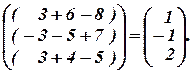
Проверка:
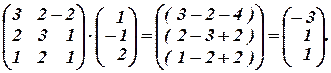
2) Найти матрицу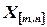 
из уравнения
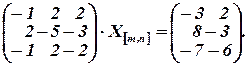
Решение.
Сначала убеждаемся в том, что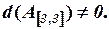 
Прежде всего необходимо найти размерность матрицы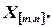 
Число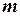 
строк в матрице 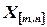должно быть равно числу столбцов в матрице, на которую матрица 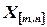умножается слева: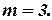 
Число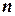 
столбцов в матрице 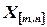равно числу столбцов в матрице произведения: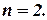 
Обозначим
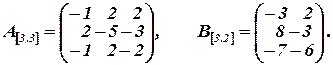
Найдем матрицу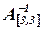 
:
.
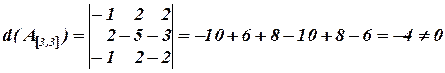Вычислим алгебраические дополнения:
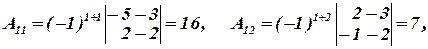
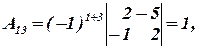
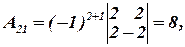
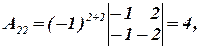
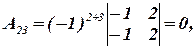
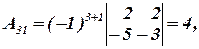
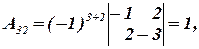
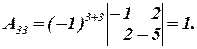
Составим присоединенную матрицу:
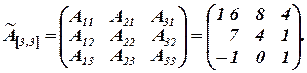
Рассчитаем обратную матрицу:
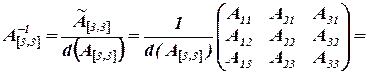
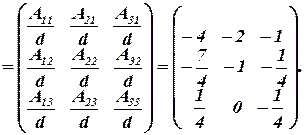
Умножив исходное уравнение на обратную матрицу слева, получим:
,
,
=
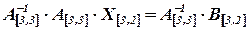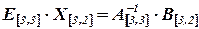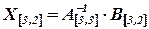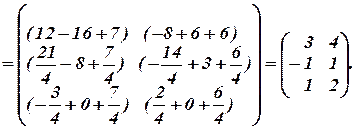
Проверка:
.
= 
= 
.
▲
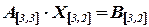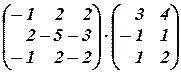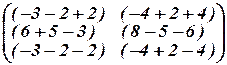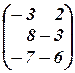Решение системы линейных уравнений
Методом Жордана-Гаусса
Пусть определенная система линейных уравнений задана расширенной матрицей:
.
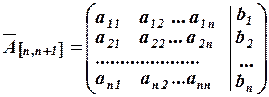Над строками расширенной матрицы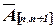 
можно осуществить следующие преобразования:
1) перестановка двух строк;
2) умножение строки на любое число, отличное от нуля;
3) прибавление к одной строке другой строки, умноженной на некоторое число.
Данные преобразования, по аналогии с используемыми ранее для расчета определителя и обратной матрицы, называются эквивалентными, так как после их осуществления решение системы линейных уравнений не изменится. Тогда исходная и преобразованная системы линейных уравнений будут эквивалентными.
С помощью эквивалентных преобразований левую часть расширенной матрицы – матрицу из коэффициентов определенной системы линейных уравнений методом Жордана-Гаусса можно привести к виду единичной матрицы, то есть получить решение. Рассмотрим суть этого метода на примере.
▼
Пример
Решить методом Жордана-Гаусса систему линейных уравнений:
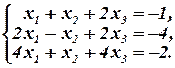
Решение.
Сначала убеждаемся в том, что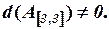
Составим расширенную матрицу:
.
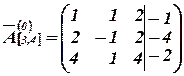1 итерация.
В качестве направляющего элемента выбираем элемент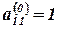 
. Преобразуем первый столбец в единичный. Для этого к второй и третьей строкам прибавляем первую строку, соответственно умноженную на –2 и –4. Получим матрицу:
.
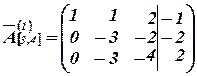На этом первая итерация закончена.
2 итерация.
Выбираем направляющий элемент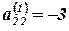 
. Так как 
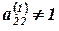, то делим вторую строку на –3. Затем умножаем вторую строку на -1 и 3 и складываем соответственно с первой и третьей строками. Получим матрицу:
.
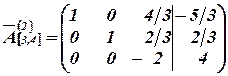3 итерация.
Выбираем направляющий элемент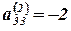 
. Так как 
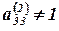, то делим вторую строку на –2. Преобразуем третий столбец в единичный. Для этого умножаем третью строку на –4/3 и –2/3 и складываем соответственно с первой и второй строками. Получим матрицу:
.
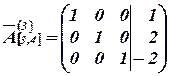Откуда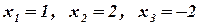 
.
▲
Вопросы для самопроверки
¨ Что представляет собой матрица?
¨ Чем являются строки и столбцы матрицы?
¨ Что называют k-мерным вектором?
¨ Как вектор может быть представлен матрицей?
¨ Чем различаются действия над векторами и над матрицами?
¨ Могут ли суммироваться матрицы разной размерности?
¨ Что представляет собой сумма двух матриц?
¨ Как находится произведение матрицы на число?
¨ В каком случае одна матрица может быть умножена на другую матрицу?
¨ Что называется произведением матрицы на матрицу?
¨ Какая матрица называется квадратной?
¨ Какая матрица называется единичной?
¨ Какими свойствами обладает умножение на единичную матрицу?
¨ Как система линейных уравнений может быть записана в виде одного матричного уравнения?
¨ Какая матрица называется расширенной?
¨ Что является определителем матрицы?
¨ У каких матриц могут быть определители?
¨ По какому правилу вычисляется определитель второго порядка?
¨ Как вычисляется определитель третьего порядка?
¨ Как схематично обозначаются в определителе произведения элементов, которые берутся со знаком плюс (со знаком минус)?
¨ При вычислении определителя n-ого порядка сколько произведений элементов матрицы алгебраически суммируется?
¨ Что означает вычисление определителей высоких порядков понижением порядка?
¨ Что называется минором элемента определителя?
¨ Что называется алгебраическим дополнением элемента определителя?
¨ Как можно выразить величину определителя через элементы его строки и их алгебраические дополнения?
¨ Что называется разложением определителя по его столбцу?
¨ Как можно упростить вычисление определителя матрицы, предварительно используя эквивалентные преобразования этой матрицы?
¨ Какое эквивалентное преобразование матрицы не влияет на величину ее определителя?
¨ Что является признаком определенности системы линейных уравнений?
¨ Как находится единственное решение определенной системы линейных уравнений по правилу Крамера?
¨ Какая квадратная матрица называется вырожденной (особенной)?
¨ Какая матрица называется обратной?
¨ Существует ли обратная матрица для вырожденной матрицы?
¨ Какая матрица называется присоединенной (взаимной)?
¨ Как с помощью присоединенной матрицы может быть вычислена обратная матрица?
¨ Как можно вычислить обратную матрицу с помощью преобразований Жордана-Гаусса?
¨ Как находится решение системы линейных уравнений с помощью обратной матрицы?
¨ Какие условия должны быть выполнены для того, чтобы найти решение системы линейных уравнений с помощью обратной матрицы?
¨ Как находится решение системы линейных уравнений методом Жордана-Гаусса?