Проверить, что матрицаневырождена и найти
Лабораторная работа № 3
Матрицы, действия над ними
Пример 1.
Вычислить матрицу, гдеи.
Введем матрицы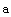 
и 
:
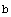В программе Mathematica есть несколько способов ввести матрицу. Первый способ: щелкните по 
выберите пункт 
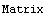и введите число строк и столбцов. Второй способ: непосредственно ввести с клавиатуры. Матрицу 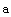введем первым способом, а матрицу 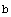- вторым:
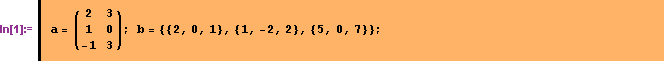
Вычислим матрицу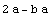 
.
Команда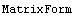 
выдает результат в матричной форме, точка между матрицами означает матричное умножение, если эту точку убрать, Mathematica будет пытаться произвести поэлементное умножение.
Хорошим тоном считается очищать значения переменных, которые не нужны для дальнейших вычислений.
Пример 2.
Проверить, что матрицыиперестановочны, а матрицыинеперестановочны.
Введем матрицы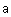 
, 
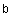и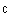 
.
Точка с запятой после каждого оператора показывает программе Mathematica, что не нужно выводить на экран результат вычислений.
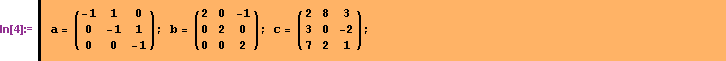
Сравним матрицы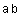 
и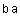 
.
В программе Mathematica оператор сравнения задается двойным равенством, одинарное равенство - это оператор присваивания.
Программа выдала 
- следовательно матрицы перестановочны.
Теперь сравним матрицы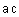 
и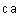 
.
Программа выдала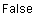 
- следовательно матрицы неперестановочны.
А какие матрицы являются перестановочными или для каких матриц умножение коммутативно?
Можно непосредственно проверить, что 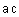не равно .
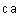Очистим значения 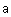, 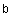и .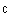
Пример 3.
Умножение матрицына единичную, скалярную и матрицыи.
Введем матрицу .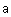
Введем матрицы единичную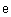 
и скалярную 
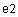с помощью встроенной функции IdentityMatrix.
Функция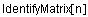 
определяет единичную матрицу размера 
.
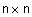Умножение матрицы 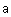на единичную матрицу:
Умножение матрицы 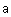на число на скалярную матрицу дает один и тот же результат.
Таким образом, умножением матрицы на скалярную матрицу можно реализовать операцию умножения матрицы на число.
Перестановка строк и столбцов матрицы осуществляется умножением на матрицы специального вида. Покажем это на примере матрицы .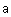
Определим матрицы 
и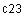 
:
Перестановка двух строк матрицы .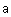
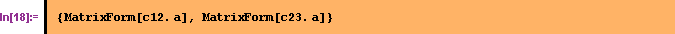
Перестановка двух столбцов матрицы .
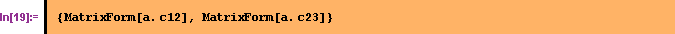
Очистим значения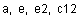 
и .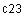
Пример 4.
Для матрицынайти.
Введем матрицу .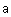
Возведем матрицу 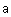в степени 0, 1 и 2 с помощью функции MatrixPower.
Очистим переменную .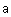
Пример 5.
Проверить, что матрицаневырождена и найти.
Введем матрицу .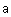
Функция Inverse находит обратную матрицу.
Можно представить эту матрицу в десятичном виде с помощью функции N.
Символ % подставляет вместо себя результат последнего вычисления.
Если матрица вырожденная, то функция 
выдаст сообщение о том, что матрица вырожденная. Но вы можете сначала посчитать определитель матрицы с помощью функции Det.
Очистим значение .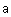
Пример 6.