Фазовые координаты управления
Фазовые координаты и управления.
Типичными примерами дифференциальных игр являются сражения, воздушные бои, преследование судна торпедой, перехват самолета зенитной ракетой, охрана объектов. Если один из игроков выключается из игры, мы получаем обычную задачу максимизации. Она уже относится к вариационному исчислению и составляет основную часть теории управления.
Решения игроков всегда заключаются в выборе некоторых величин, называемых управлениями. Они в свою очередь определяют собой значения других величин - фазовых координат. Последние обладают тем свойством, сто знание их значений в любой момент времени полностью определяет течение игры.
Военные игры.
Фазовые координаты должны быть такими величинами, которые характеризуют положение дел в той мере, в какой по необходимости упрощенная модель задачи соответствует реальному процессу. Фазовыми координатами могут, в частности, быть число людей, самолетов, танков, судов; может оказаться целесообразным разделить их на группы по расположению в различных районах или по какому-либо другому признаку, например по удаленности от линии фронта и т.д.
Выбор управлений часто обусловлен обстоятельствами. скорость изменения фазовых координат является заданной функцией от фазовых координат и управлений обоих игроков.
Уравнение движения
Уравне́ние движе́ния (уравнения движения) — уравнение или система уравнений, задающие закон эволюции механической или сходной динамической системы (например, поля) во времени[1].
Эволюция физической системы однозначно определяется уравнениями движения и начальными условиями. В уравнения движения динамической системы входит полный набор переменных, определяющий состояние этой системы (например, все координаты и скорости, или все координаты и импульсы), а также их производные по времени, что позволяет, зная такой набор в некий момент времени, вычислить его для момента времени, отстоящего на малый (бесконечно малый) промежуток времени. В принципе, повторяя этот процесс вычисления последовательно большое (бесконечное) количество раз, можно вычислить значение всех этих переменных для момента времени, как угодно[2] далеко отстоящего от начального. С помощью такого процесса можно (выбрав 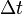 достаточно малым, но конечным) получить приближенное численное решение уравнений движения. Однако чтобы получить точное[3] решение, приходится применять другие математические методы.
достаточно малым, но конечным) получить приближенное численное решение уравнений движения. Однако чтобы получить точное[3] решение, приходится применять другие математические методы.
В современной квантовой теории термин уравнение движения нередко используется для обозначения именно только классических уравнений движения, то есть как раз для различения классического и квантового случая. В таком употреблении, например, слова «решение уравнений движения» означают именно классическое (неквантовое) приближение, которое может затем так или иначе использоваться при получении квантового результата или для сравнения с ним.
