Общие условия существования интеграла Стилтьеса
Определение интеграла Стилтьеса.
Стилтьес Томас Иоаннес (29.21.1856, Эволле-31.12.1894, Тулуза) нидерландский ученый математик и астроном, член Нидерландской академии наук, иностранный член-корреспондент Санкт-Петербургской академии наук по Физико-математическому отделению. Окончил Политехническую школу в Делфте. Работал на Лейденской обсерватории, с 1886 года преподаватель, затем профессор Университета в Тулузе. Научные исследования Стилтьеса в основном касаются теории функциональных непрерывных дробей, проблемы моментов, теории ортогональных многочленов, интегрального преобразования, приближенного интегрирования и других вопросов классического анализа. Обобщенное Стилтьесам понятие интеграла Г.Римана, предложенное в 1894 году, играет важную роль в современной математике.
Определяется интеграл Стилтьеса следующим образом.
Пусть в промежутке [a
,
b] заданы две ограниченные функции f
(
x
) и g
(
x
). Разложим точками
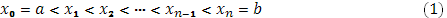
промежуток [a
,
b] на части и положим 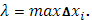 Выбрав в каждой из частей
Выбрав в каждой из частей 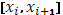 (i=0, 1,…,n-1) по каждой точке
(i=0, 1,…,n-1) по каждой точке 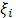 , вычислим значение f
, вычислим значение f
( 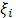 ) функции f
) функции f
(
x
) и умножим его на соответствующее промежутку 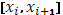 приращение функции g
приращение функции g
(
x
)
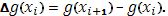
Наконец, составим сумму всех таких произведений:

Эта сумма носит название интегральной суммы Стилтьеса.
Конечный предел суммы Стилтьеса 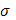 при стремлении
при стремлении 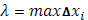 к нулю называется интегралом Стилтьеса функции f
к нулю называется интегралом Стилтьеса функции f
(
x
) по функции g
(
x
) и обозначается символом
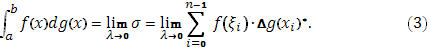
Чтобы особенно отчетливо подчеркнуть, что интеграл рассматривается в смысле Стилтьеса, употребляют обозначение
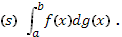
Предел здесь понимается в том смысле, что и в случае обыкновенного определенного интеграла.
Точнее говоря, число I называется интегралом Стилтьеса, если для любого числа 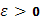 существует такое число
существует такое число 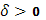 , что лишь только промежуток [a
, что лишь только промежуток [a
,
b] раздроблен на части так, что 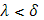 , тотчас же выполняется неравенство
, тотчас же выполняется неравенство
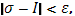
Как бы ни выбирать точки 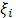 в соответствующих промежутках.
в соответствующих промежутках.
При существовании интеграла (3) говорят также, что функция f
(
x
) в промежутке [a
,
b] интегрируема по функции 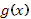 .
.
Единственное (но существенное) отличие данного выше определения от обычного определения интеграла Римана состоит в том, что 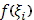 умножается не на приращение
умножается не на приращение 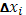 независимой переменной, а на приращение
независимой переменной, а на приращение 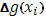 второй функции. Таким образом, интеграл Римана есть частный случай интеграла Стилтьеса, когда в качестве функции
второй функции. Таким образом, интеграл Римана есть частный случай интеграла Стилтьеса, когда в качестве функции 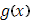 взята сама независимая переменная x:
взята сама независимая переменная x:
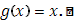
Мы для определенности предполагали a<b; нетрудно аналогично рассмотреть и случай, когда a>b. Впрочем, он непосредственно приводится к предыдущему ввиду равенства
продолжение
Общие условия существования интеграла Стилтьеса.
Установим общие условия существования интеграла Стилтьеса, ограниченность, впрочем, предположением, что функция  монотонно возрастает.
монотонно возрастает.
Отсюда следует, что при a<b теперь все 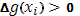 , наподобие того, как раньше было
, наподобие того, как раньше было 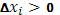 . Аналогично сумма Дарбу, здесь целесообразно ввести сумм
. Аналогично сумма Дарбу, здесь целесообразно ввести сумм

где означают, соответственно, нижнюю и верхнюю точные границы функции f
(
x
) в i-ом промежутке 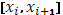 . эти суммы мы будем называть нижней и верхней суммами Дарбу - Стилтьеса.
. эти суммы мы будем называть нижней и верхней суммами Дарбу - Стилтьеса.
При одном и том же разбиении 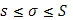 , причем s и S служат точными границами для стилтьесовых сумм
, причем s и S служат точными границами для стилтьесовых сумм 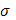 . Сами суммы Дарбу – Стилтьеса обладают следующими свойствами:
. Сами суммы Дарбу – Стилтьеса обладают следующими свойствами:
1-е свойство: Если к имеющимся точкам деления добавить новые точки, то нижняя сумма Дарбу – Стилтьеса может от этого разве лишь возрасти, а верхняя сумма – разве лишь уменьшится.
2-е свойство: Каждая нижняя сумма Дарбу – Стилтьеса не превосходит каждой верхней суммы, хотя бы и отвечающей другому разбиению промежутка.
Если ввести нижний и верхний интегралы Дарбу – Стилтьеса:
то оказывается, что
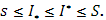
Наконец, с помощью сумм Дарбу – Стилтьеса легко устанавливается для рассматриваемого случая основной признак существования интеграла Стилтьеса:
Теорема. Для существования интеграла Стилтьеса необходимо и достаточно, чтоб было
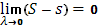
или

если под 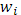 понимать колебание
понимать колебание 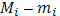 функции f
функции f
(
x
) в i-ом промежутке 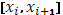 .
.
