Уравнения, разрешенные относительно производной. Простейшие методы
Интегрирования
2.1 Уравнения с разделенными и разделяющимися переменными
§ Уравнения с разделенными переменными имеют вид

Эквивалентная запись уравнения:  (правая часть уравнения зависит только от х, а левая – только от у). Общее решение получается почленным интегрированием:
(правая часть уравнения зависит только от х, а левая – только от у). Общее решение получается почленным интегрированием:
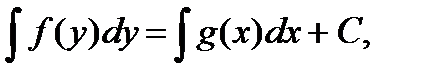
где С – произвольная постоянная.
П р и м е р 1. Решить уравнение 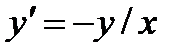 .
.
Записав уравнение в виде  и представив это как
и представив это как 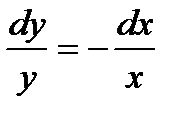 , интегрируя имеем
, интегрируя имеем
 или у = С/х. Решением является также у = 0.
или у = С/х. Решением является также у = 0.
§ Уравнения с разделяющимися переменными имеют вид
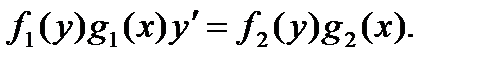
Делим обе части на 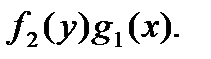 В результате приходим к уравнению с разделенными переменными. После интегрирования получим
В результате приходим к уравнению с разделенными переменными. После интегрирования получим
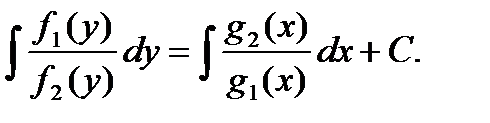
Замечание. При почленном делении уравнения на  могут быть потеряны решения, обращающие функцию
могут быть потеряны решения, обращающие функцию 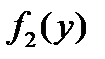 в нуль, а также решение вида х = а , где
в нуль, а также решение вида х = а , где  .
.
П р и м е р 2. Проинтегрировать уравнение 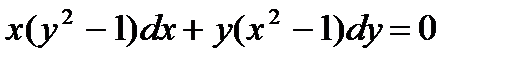 .
.
Разделяем переменные  Интегрируя находим
Интегрируя находим 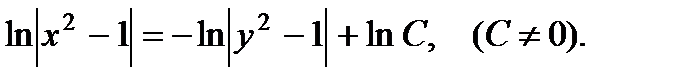 Откуда
Откуда 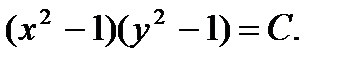
При делении на 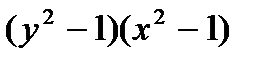 могли быть потеряны решения
могли быть потеряны решения 
2.2 Уравнение вида 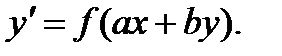
Замена 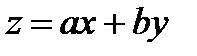 приводит данное уравнение к уравнению с разделенными переменными
приводит данное уравнение к уравнению с разделенными переменными  см. разд. 2.1.
см. разд. 2.1.
2.3 Однородные уравнения и приводящиеся к ним
§ Однородные уравнения не меняются при одновременном растяжении
(сжатии) независимой и зависимой переменных по правилу:  где
где  - произвольная постоянная
- произвольная постоянная  Они могут быть записаны в виде
Они могут быть записаны в виде 
Замена 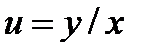 приводит однородное уравнение к уравнению с разделяющимися переменными
приводит однородное уравнение к уравнению с разделяющимися переменными 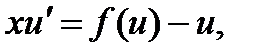 см. разд. 2.1
см. разд. 2.1
П р и м е р 3. Решить уравнение 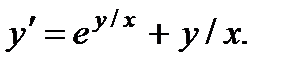
Подстановка  приводит это уравнение к виду
приводит это уравнение к виду 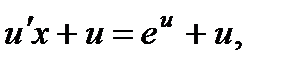 или
или 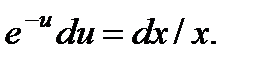 Интегрируя находим
Интегрируя находим  и
и 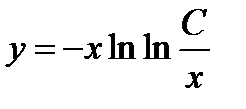 .
.
§ К однородному уравнению приводится уравнение
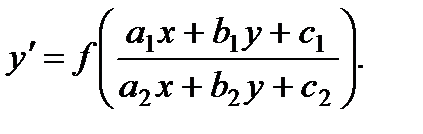
При  надо перейти к новым переменным
надо перейти к новым переменным  где постоянные
где постоянные 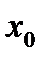 и
и  определяем путем решения линейной алгебраической системы
определяем путем решения линейной алгебраической системы

В результате для функции 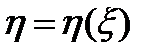 получим уравнение
получим уравнение

Последнее после деления числителя и знаменателя аргумента функции f на 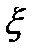 принимает вид однородного уравнения, правая часть которого зависит только от отношения переменных
принимает вид однородного уравнения, правая часть которого зависит только от отношения переменных 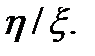
При  см. уравнение из разд. 2.2.
см. уравнение из разд. 2.2.
П р и м е р 4. Решить уравнение 
Находим точку пересечения прямых, полученных приравниванием к нулю числителя и знаменателя:
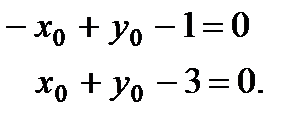
Откуда х0 =1, у0 = 2. После замены  уравнение принимает вид
уравнение принимает вид
 или
или 
Получилось однородное уравнение, которое решается заменой  В результате находим
В результате находим
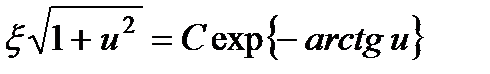 .
.
Возводя в квадрат и возвращаясь к старым переменным, имеем

2.4 Обобщенно-однородные уравнения и приводящиеся к ним
§ Обобщенно-однородные уравнения не меняются при одновременном
растяжении (сжатии) независимой и зависимой переменных по правилу: 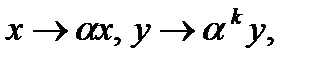 где
где 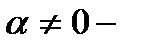 произвольная постоянная, а k – некоторое число. Они могут быть записаны в виде
произвольная постоянная, а k – некоторое число. Они могут быть записаны в виде
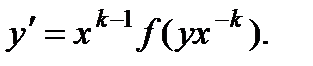
Замена и = ух-k приводит обобщенно-однородное уравнение к уравнению с разделяющимися переменными 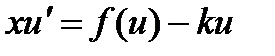 , см. разд. 2.1.
, см. разд. 2.1.
§ К обобщенно-однородному уравнению сводится уравнение
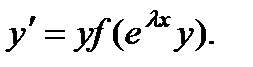
Для этого надо сделать замену z = ex и положить 
2.5 Линейное уравнение
Линейное уравнение первого порядка имеет вид
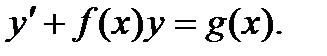
Решение ищем в виде произведения y = uv , где функция v = v(x) удовлетворяет «укороченному» уравнению  [в качестве такой функции можно взять частное решение v = e-F, где
[в качестве такой функции можно взять частное решение v = e-F, где 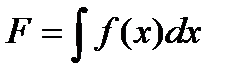 ]. Для функции и = и(х) получим уравнение с разделяющимися переменными
]. Для функции и = и(х) получим уравнение с разделяющимися переменными 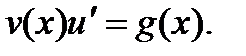 Интегрируя уравнение для и , находим общее решение
Интегрируя уравнение для и , находим общее решение
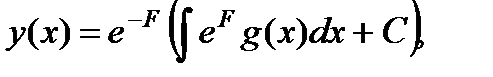 где
где 
П р и м е р 5. Решить задачу Коши: 
Записываем это линейное уравнение в стандартном виде

Полагая y = u z , получим 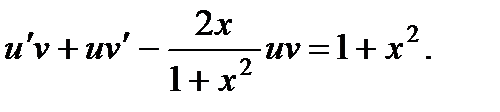
Сгруппировав слагаемые, получим два уравнения:
 и
и 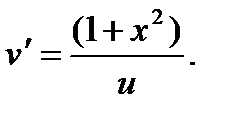
Записываем первое в виде  , откуда и = х2 + 1. Подставляя это во второе уравнение, находим
, откуда и = х2 + 1. Подставляя это во второе уравнение, находим 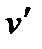 = 1 или v = х + C. Подставляя сюда х = 1, у = 2, получим С = 0. Решение задачи Коши имеет вид у = х(х2+1).
= 1 или v = х + C. Подставляя сюда х = 1, у = 2, получим С = 0. Решение задачи Коши имеет вид у = х(х2+1).
2.6 Уравнение Бернулли
Уравнение Бернулли имеет вид

Подстановка z = y1-a приводит его к линейному уравнению 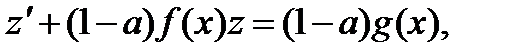 которое рассматривается в разд.2.5. Учитывая сказанное, получим общий интеграл
которое рассматривается в разд.2.5. Учитывая сказанное, получим общий интеграл
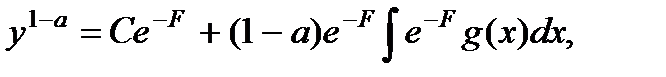 где
где 
П р и м е р 6. Проинтегрировать уравнение 
Здесь а =1/2, тогда замена у = z2 приводит данное уравнение Бернулли к линейному уравнению 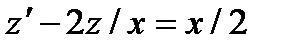 интегрируя которое находим
интегрируя которое находим  , следовательно
, следовательно  .
.
2.7 Уравнение вида 
Замена и = у / х приводит данное уравнение к уравнению с разделяющимися переменными 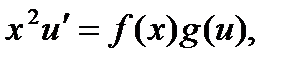 см. разд. 2.1.
см. разд. 2.1.
