Теорема о производной сложной функции
Пусть y = f(u), а u= u(x). Получаем функцию y, зависящую от аргумента x: y = f(u(x)). Последняя функция называется функцией от функции или сложной функцией.
Областью определения функции y = f(u(x)) является либо вся область определения функции u=u(x) либо та ее часть, в которой определяются значения u, не выходящие из области определения функции y= f(u).
Операция "функция от функции" может проводиться не один раз, а любое число раз.
Установим правило дифференцирования сложной функции.
Теорема. Если функция u= u(x) имеет в некоторой точке x0 производную 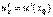 и принимает в этой точке значение u0 = u(x0), а функция y= f(u) имеет в точке u0производную y 'u= f '(u0), то сложная функция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y 'x= f '(u0)·u '(x0), где вместо u должно быть подставлено выражение u= u(x).
и принимает в этой точке значение u0 = u(x0), а функция y= f(u) имеет в точке u0производную y 'u= f '(u0), то сложная функция y = f(u(x)) в указанной точке x0 тоже имеет производную, которая равна y 'x= f '(u0)·u '(x0), где вместо u должно быть подставлено выражение u= u(x).
Таким образом, производная сложной функции равна произведению производной данной функции по промежуточному аргументу u на производную промежуточного аргумента по x.
Доказательство. При фиксированном значении х0 будем иметь u0=u(x0), у0=f(u0). Для нового значения аргумента x0+Δx:
Δu= u(x0 + Δx) – u(x0), Δy=f(u0+Δu) – f(u0).
Т.к. u – дифференцируема в точке x0, то u – непрерывна в этой точке. Поэтому при Δx→0 Δu→0. Аналогично при Δu→0 Δy→0.
По условию 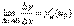 . Из этого соотношения, пользуясь определением предела, получаем (при Δu→0)
. Из этого соотношения, пользуясь определением предела, получаем (при Δu→0)
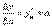 ,
,
где α→0 при Δu→0, а, следовательно, и при Δx→0.
Перепишем это равенство в виде:
Δy= y 'uΔu+α·Δu.
Полученное равенство справедливо и при Δu=0 при произвольном α, так как оно превращается в тождество 0=0. При Δu=0 будем полагать α=0. Разделим все члены полученного равенства на Δx
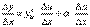 .
.
По условию 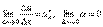 . Поэтому, переходя к пределу при Δx→0, получим y 'x= y 'u·u 'x . Теорема доказана.
. Поэтому, переходя к пределу при Δx→0, получим y 'x= y 'u·u 'x . Теорема доказана.
Итак, чтобы продифференцировать сложную функцию y = f(u(x)), нужно взять производную от "внешней" функции f, рассматривая ее аргумент просто как переменную, и умножить на производную от "внутренней" функции по независимой переменной.
Если функцию y=f(x) можно представить в виде y=f(u), u=u(v), v=v(x), то нахождение производной y 'x осуществляется последовательным применением предыдущей теоремы.
По доказанному правилу имеем y 'x= y 'u·u 'x . Применяя эту же теорему для u 'x получаем 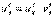 , т.е.
, т.е.
y 'x = y 'x· u 'v· v 'x = f 'u (u)·u 'v (v)·v 'x (x).
Примеры.
1. y = sin x2. Тогда 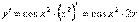 .
.
2. 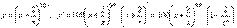
3. 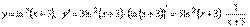

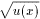 )' = u'(x)/2
)' = u'(x)/2 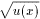 ; 2. (logau(x))' = (u'(x)logae)/u(x) при 0<a№1, u(x)>0, в частности, (ln u(x))' = u'(x)/u(x); 3. (au(x))' = au(x)ln a u'(x) при 0<a№1, в частности, (eu(x))' = u'(x)eu(x); 4. (sin u(x))' = cos u(x)u'(x); 5. (cos u(x))' = -sin u(x)u'(x); 6. (tg u(x))' = u'(x)/cos2u(x) x№ p/2+p n, n=0,+-1,...; 7. (ctg u(x))' = -u'(x)/sin2u(x) x№ p n, n=0,+-1,...; 8. (arcsin u(x))' = u'(x)/
; 2. (logau(x))' = (u'(x)logae)/u(x) при 0<a№1, u(x)>0, в частности, (ln u(x))' = u'(x)/u(x); 3. (au(x))' = au(x)ln a u'(x) при 0<a№1, в частности, (eu(x))' = u'(x)eu(x); 4. (sin u(x))' = cos u(x)u'(x); 5. (cos u(x))' = -sin u(x)u'(x); 6. (tg u(x))' = u'(x)/cos2u(x) x№ p/2+p n, n=0,+-1,...; 7. (ctg u(x))' = -u'(x)/sin2u(x) x№ p n, n=0,+-1,...; 8. (arcsin u(x))' = u'(x)/  , -1<u(x)<1; 9. (arccos u(x))' = -u'(x)/
, -1<u(x)<1; 9. (arccos u(x))' = -u'(x)/  , -1<u(x)<1; 10. (arctg u(x))' = u'(x)/(1+u2(x)); 11. (arcctg u(x))' = -u'(x)/(1+u2(x)). Введем гиперболические функции: sh x = (1/2)(ex-e-x)- гиперболический синус; ch x = (1/2)(ex+ex)- гиперболический косинус; th x = sh x/ch x -гиперболический тангенс; cth x = ch x/sh x - гиперболический котангенс. Из определения гиперболических функций элементарно вытекают следующие формулы для нахождения их производных. 1. (sh x)' = ch x; 2. (ch x)' = sh x; 3. (th x)' = 1/ch2 x; 4. (cth x)' = -1/sh2 x. Пример 7. Найти y', если 1. y(x) = x3arcsin x.
, -1<u(x)<1; 10. (arctg u(x))' = u'(x)/(1+u2(x)); 11. (arcctg u(x))' = -u'(x)/(1+u2(x)). Введем гиперболические функции: sh x = (1/2)(ex-e-x)- гиперболический синус; ch x = (1/2)(ex+ex)- гиперболический косинус; th x = sh x/ch x -гиперболический тангенс; cth x = ch x/sh x - гиперболический котангенс. Из определения гиперболических функций элементарно вытекают следующие формулы для нахождения их производных. 1. (sh x)' = ch x; 2. (ch x)' = sh x; 3. (th x)' = 1/ch2 x; 4. (cth x)' = -1/sh2 x. Пример 7. Найти y', если 1. y(x) = x3arcsin x. 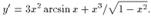 2. y(x) = ln sin (x2+1). y' = (2xcos(x2+1))/sin(x2+1) = 2x ctg(x2+1) Замечание. Производная любой элементарной функции является элементарной функцией, то есть операция дифференцирования не выводит из класса элементарных функций. МуТНый 26 Непрерывность функции, имеющей производную. Теорема. Если функция y = f(x) дифференцируема в некоторой точке x = x0, то она в этой точке непрерывна. Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x0 функция y = f(x) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x| непрерывна для всех x (–Ґ < х < Ґ), но в точке x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x. 1.
2. y(x) = ln sin (x2+1). y' = (2xcos(x2+1))/sin(x2+1) = 2x ctg(x2+1) Замечание. Производная любой элементарной функции является элементарной функцией, то есть операция дифференцирования не выводит из класса элементарных функций. МуТНый 26 Непрерывность функции, имеющей производную. Теорема. Если функция y = f(x) дифференцируема в некоторой точке x = x0, то она в этой точке непрерывна. Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x0 функция y = f(x) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x| непрерывна для всех x (–Ґ < х < Ґ), но в точке x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают. ОСНОВНЫЕ ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ Применяя общий способ нахождения производной с помощью предела можно получить простейшие формулы дифференцирования. Пусть u=u(x),v=v(x) – две дифференцируемые функции от переменной x. 1. 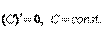 2.
2. 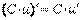 . 3.
. 3. 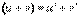 (справедлива для любого конечного числа слагаемых). 4.
(справедлива для любого конечного числа слагаемых). 4. 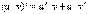 . 5.
. 5. 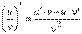 . а)
. а) 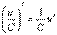 . б)
. б) 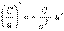 . Формулы 1 и 2 докажите самостоятельно. Доказательство формулы 3. Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx). Тогда Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv. Следовательно,
. Формулы 1 и 2 докажите самостоятельно. Доказательство формулы 3. Пусть y = u(x) + v(x). Для значения аргумента x+Δx имеем y(x+Δx)=u(x+Δx) + v(x+Δx). Тогда Δy=y(x+Δx) – y(x) = u(x+Δx) + v(x+Δx) – u(x) – v(x) = Δu +Δv. Следовательно, 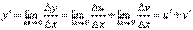 . Доказательство формулы 4. Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x+Δx), поэтому Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x). Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u(x+Δx)→u(x), v(x+Δx)→v(x), при Δx→0. Поэтому можем записать
. Доказательство формулы 4. Пусть y=u(x)·v(x). Тогда y(x+Δx)=u(x+Δx)·v(x+Δx), поэтому Δy=u(x+Δx)·v(x+Δx) – u(x)·v(x). Заметим, что поскольку каждая из функций u и v дифференцируема в точке x, то они непрерывны в этой точке, а значит u(x+Δx)→u(x), v(x+Δx)→v(x), при Δx→0. Поэтому можем записать 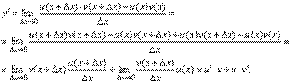 На основании этого свойства можно получить правило дифференцирования произведения любого числа функций. Пусть, например, y=u·v·w. Тогда, y ' = u '·(v·w) + u·(v ·w) ' = u '·v·w + u·(v '·w +v·w ') = u '·v·w + u·v '·w + u·v·w '. Доказательство формулы 5. Пусть
На основании этого свойства можно получить правило дифференцирования произведения любого числа функций. Пусть, например, y=u·v·w. Тогда, y ' = u '·(v·w) + u·(v ·w) ' = u '·v·w + u·(v '·w +v·w ') = u '·v·w + u·v '·w + u·v·w '. Доказательство формулы 5. Пусть 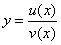 . Тогда
. Тогда 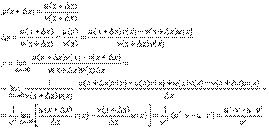 При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0. Примеры. 1. Если
При доказательстве воспользовались тем, что v(x+Δx)→v(x) при Δx→0. Примеры. 1. Если 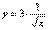 , то
, то 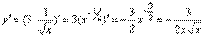 2. y = x3 – 3x2 + 5x + 2. Найдем y '(–1). y ' = 3x2 – 6x+ 5. Следовательно, y '(–1) = 14. 3. y = ln x · cos x, то y ' = (ln x) ' cos x + ln x (cos x) ' =1/x∙cos x – ln x · sin x. 4.
2. y = x3 – 3x2 + 5x + 2. Найдем y '(–1). y ' = 3x2 – 6x+ 5. Следовательно, y '(–1) = 14. 3. y = ln x · cos x, то y ' = (ln x) ' cos x + ln x (cos x) ' =1/x∙cos x – ln x · sin x. 4. 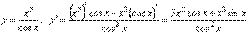 5.
5.  Таким образом,
Таким образом, 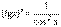 6. Аналогично для y= ctgx,
6. Аналогично для y= ctgx, 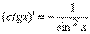 ТЕОРЕМА О ПРОИЗВОДНОЙ ОБРАТНОЙ ФУНКЦИИ Докажем теорему, позволяющую находить производную функции y=f(x), зная производную обратной функции. Теорема. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у0 имеет производную g '(v0), отличную от нуля, то в соответствующей точке x0=g(x0) функция y=f(x) имеет производную f '(x0), равную
ТЕОРЕМА О ПРОИЗВОДНОЙ ОБРАТНОЙ ФУНКЦИИ Докажем теорему, позволяющую находить производную функции y=f(x), зная производную обратной функции. Теорема. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у0 имеет производную g '(v0), отличную от нуля, то в соответствующей точке x0=g(x0) функция y=f(x) имеет производную f '(x0), равную 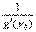 , т.е. справедлива формула
, т.е. справедлива формула 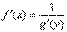 . Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0. Покажем, что
. Доказательство. Т.к. x=g(y) дифференцируема в точке y0, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x0=g(y0). Следовательно, при Δx→0 Δy→0. Покажем, что 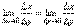 . Пусть
. Пусть 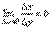 . Тогда по свойству предела
. Тогда по свойству предела 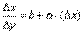 . Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е.
. Перейдем в этом равенстве к пределу при Δy→0. Тогда Δx→0 и α(Δx)→0, т.е. 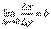 . Следовательно,
. Следовательно, 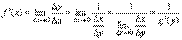 , что и требовалось доказать. Эту формулу можно записать в виде
, что и требовалось доказать. Эту формулу можно записать в виде 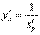 . Рассмотрим применение этой теоремы на примерах. Примеры. 1. y = ex. Обратной для этой функции является функция x= ln y. Мы уже доказали, что
. Рассмотрим применение этой теоремы на примерах. Примеры. 1. y = ex. Обратной для этой функции является функция x= ln y. Мы уже доказали, что 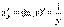 . Поэтому согласно сформулированной выше теореме
. Поэтому согласно сформулированной выше теореме 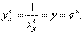 Итак,
Итак, | (ex) ' = ex |
2. Аналогично можно показать, что (ax) ' = ax·lna. Докажите самостоятельно.
3. y = arcsin x. Рассмотрим обратную функцию x = sin y. Эта функция в интервале – π/2<y<π/2 монотонна. Ее производная x ' = cos y не обращается в этом интервале в нуль. Следовательно, по теореме о производной обратной функции
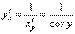 .
.
Но на (–π/2; π/2)  .
.
Поэтому 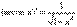
4. Аналогично 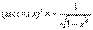
Докажите самостоятельно.
y = arctg x. Эта функция по определению удовлетворяет условию существования обратной функции на интервале –π/2< y < π/2. При этом обратная функция x = tg yмонотонна. По ранее
Если 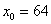 , то приращение аргумента:
, то приращение аргумента: 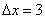 .
.
Итак, число 67 представлено в виде суммы 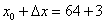
Далее работаем с правой частью формулы 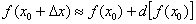 .
.
Сначала вычислим значение функции в точке 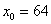 . Собственно, это уже сделано ранее:
. Собственно, это уже сделано ранее:
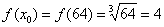
Дифференциал в точке находится по формуле:
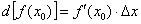 – тоже можете переписать к себе в тетрадь.
– тоже можете переписать к себе в тетрадь.
Из формулы следует, что нужно взять первую производную:
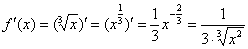
И найти её значение в точке  :
:
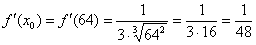
Таким образом:
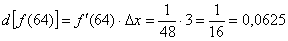
Всё готово! Согласно формуле 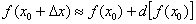 :
:
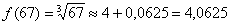
Найденное приближенное значение достаточно близко к значению 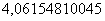 , вычисленному с помощью микрокалькулятора.
, вычисленному с помощью микрокалькулятора.
Ответ: 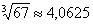
33) Производные порядка выше первого называются производными высших порядков. Начиная с производной четвёртого порядка, производные обозначают римскими цифрами или числами в скобках ( yV или y(5)– производная пятого порядка). Пусть функция y = f(x) задана неявно в виде уравнения F(x, y) 0 . Продифференцировав это уравнение по x и разрешив полученное уравнение относительно y , найдём производную первого порядка. Продифференцировав по x первую производную, получим вторую производную от неявной функции. Вторая производная зависит от x , y и y . Подставляя уже найденное значение y в
выражение второй производной, выразим y через x и y .
Аналогично поступаем для нахождения производной третьего и более высокого
порядков.
Механический смысл производной второго порядка
Пусть материальная точка М движется прямолинейно по закону S = f (t). Как уже известно,
производная S′t равна скорости точки в данный момент времени: S′t = v.
Покажем, что вторая производная от пути по времени есть величина ускорения
прямолинейного движения точки, т.е. S′′t = а.
Пусть в момент времени t скорость точки равна v, а в момент t + Δt – скорость равна v + Δv,
т.е. за промежуток времени Δt скорость изменилась на величину Δv.
Отношение Δt/Δv выражает среднее ускорение движения точки за время Δt. Предел этого
отношения при Δt → 0 называется ускорением точки М в данный момент t и обозначается
буквой а: Lim Δv/Δt=a, где Δt стремиться к 0. То есть v′ = а. Но v = S′t. Поэтому а = (S′t)′, т.е. а = S′′t
34) Производная параметрически заданной функции.
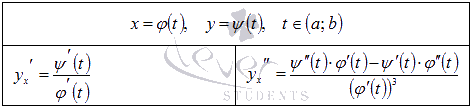
В зависимости от правила, устанавливающего зависимость между множествами значений величин x и y, различают несколько способов задания функции. Наиболее привычным является представление функции в явном виде 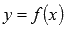 . Однако, в некоторых случаях удобно описывать функциональную зависимость множеством пар значений (x; y), которые вычисляются для каждого значения параметра t из промежутка (a; b). К примеру, все пары значений
. Однако, в некоторых случаях удобно описывать функциональную зависимость множеством пар значений (x; y), которые вычисляются для каждого значения параметра t из промежутка (a; b). К примеру, все пары значений 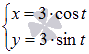 при
при 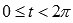 задают окружность с центром в начале координат радиуса 3.
задают окружность с центром в начале координат радиуса 3.
Наши рекомендации
