Классы случаев существования интеграла Стилтьеса
Определение функции с ограниченным изменением:
Пусть функция f
(
x
) определена в некоторомконечном промежутке [a
,
b]. Разложим этот промежуток произвольным образом на части с помощью точек деления:
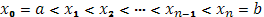
Из абсолютных величин приращений функции, отвечающих отдельным частичным промежуткам, образуем сумму
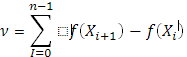
Если такие суммы в их совокупности ограничены сверху, то говорят, что функция f
(
x
) в промежутке [a
,
b] имеет ограниченное изменение ( или ограниченную вариацию). При этом точную верхниюю границу этих сумм называют полным изменением функции в указанном промежутке и обозначают символом
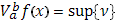
I. Если функция f
(
x
) непрерывна, а функция  имеет ограниченное изменение, то интеграл Стилтьеса
имеет ограниченное изменение, то интеграл Стилтьеса

существует.
Сначала предположим, что  монотонно возрастает: тогда применим критерий предыдущего пункта. По произвольному заданию
монотонно возрастает: тогда применим критерий предыдущего пункта. По произвольному заданию 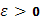 ввиду равномерной непрерывности функции f
ввиду равномерной непрерывности функции f
(
x
) найдется такое 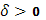 , что в любом промежутке с длиной, меньшей
, что в любом промежутке с длиной, меньшей 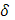 , колебание f
, колебание f
(
x
) будет меньше 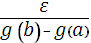 . Пусть теперь промежуток [a
. Пусть теперь промежуток [a
,
b] произвольно разбит на части так, что 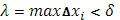 . Тогда все
. Тогда все 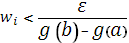 и
и
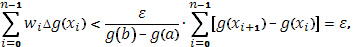
откуда и следует выполнение условия (4), а стало быть и существование интеграла.
В общем случаи, если функция  имеет ограниченное изменение, она представима в виде разности двух ограниченных возрастающих функций:
имеет ограниченное изменение, она представима в виде разности двух ограниченных возрастающих функций: 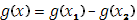 . В соответствии с этим преобразуется и сумма Стилтьеса, отвечающая функции
. В соответствии с этим преобразуется и сумма Стилтьеса, отвечающая функции 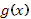 :
:
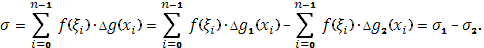
Так как каждая из сумм 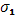 и
и 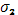 при
при 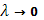 стремится к конечному пределу, то это справедливо и относительно суммы
стремится к конечному пределу, то это справедливо и относительно суммы 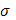 , что и требовалось доказать.
, что и требовалось доказать.
Можно ослабить условия, налагаемые на функцию f
(
x
), если одновременно усилить требования к функции 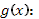
II. Если функция f
(
x
) интегрируема в [a
,
b] в смысле Римана, а 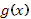 удовлетворяет условию Липшица:
удовлетворяет условию Липшица:
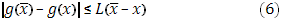
(L=const., 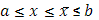 ), то интеграл существует.
), то интеграл существует.
Предположим, что функция  не только удовлетворяет условию (6), но и является монотонно возрастающей.
не только удовлетворяет условию (6), но и является монотонно возрастающей.
Ввиду (6), очевидно, 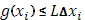 , так что
, так что
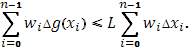
Но последняя сумма при 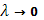 и сама стремится к 0 вследствие интегрируемости (в смысле Римана) функции f
и сама стремится к 0 вследствие интегрируемости (в смысле Римана) функции f
(
x
), а тогда стремится к нулю и первая сумма, что доказывает существование интеграла (5).
В общем случаи функции 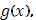 удовлетворяющей условию Липшица (6), представим ее в виде разности
удовлетворяющей условию Липшица (6), представим ее в виде разности
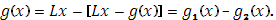
Функция 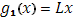 , очевидно, удовлетворяет условию Липшица и в то же время монотонно возрастает. То же справедливо и для функции
, очевидно, удовлетворяет условию Липшица и в то же время монотонно возрастает. То же справедливо и для функции 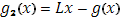 , так как, в силу (6) , при
, так как, в силу (6) , при 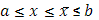
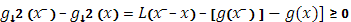
и

III
.Если функцияf
(
x) интегрируема в смысле Римана, а функция  представима в виде интеграла с переменным верхним пределом:
представима в виде интеграла с переменным верхним пределом:

где 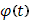 абсолютно интегрируема в промежутке [a
абсолютно интегрируема в промежутке [a
,
b], то интеграл (5) существует.
Пусть 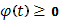 , так что монотонно возрастает. Если
, так что монотонно возрастает. Если 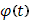 интегрируема в собственном смысле и, следовательно, ограничена:
интегрируема в собственном смысле и, следовательно, ограничена:
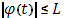 , то для
, то для  имеем
имеем
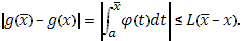
Таким образом, в этом случаи  удовлетворяет условию Липшица, и интеграл существует в силу II.
удовлетворяет условию Липшица, и интеграл существует в силу II.
Предположим теперь, что 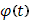 интегрируема в несобственном смысле. Ограничимся случаем одной особой точки, например, b. Прежде всего, т.к.
интегрируема в несобственном смысле. Ограничимся случаем одной особой точки, например, b. Прежде всего, т.к. 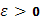 выберем
выберем 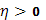 так, чтобы было
так, чтобы было

где 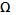 - общее колебание функции
- общее колебание функции 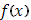 в рассматриваемом промежутке.
в рассматриваемом промежутке.
Разобьем промежуток [a
,
b] произвольным образом на части и составим сумму
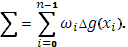
Она распадается на две суммы 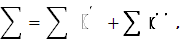 из которых первая отвечает промежуткам, целиком содержащимся в промежутке
из которых первая отвечает промежуткам, целиком содержащимся в промежутке 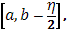 а вторая – остальным промежуткам. Последнее содержатся в промежутке [b
а вторая – остальным промежуткам. Последнее содержатся в промежутке [b
- 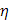 ,b],если только
,b],если только 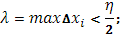 тогда, в силу (8),
тогда, в силу (8),
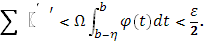
С другой стороны, так как в промежутке 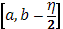 функция
функция 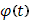 интегрируема в собственном смысле, то по доказанному при достаточно малом
интегрируема в собственном смысле, то по доказанному при достаточно малом 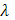 и сумма
и сумма 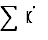 станет меньше
станет меньше 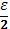 . Отсюда следует (4), что и требовалось доказать.
. Отсюда следует (4), что и требовалось доказать.
В общем случаи, когда функция 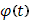 абсолютно интегрируема в промежутке [a
абсолютно интегрируема в промежутке [a
,
b]:

неотрицательные и интегрируемые в названном промежутке. Так как
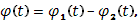
то вопрос сводится, как и выше, к уже рассмотренному случаю.
Замечание. Пусть функция  непрерывна в промежутке [a
непрерывна в промежутке [a
,
b] и имеет, исключая лишь конечное число точек, производную 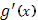 , причем эта производная (если ее значения в точках, где она не существует, выбрать произвольным образом) интегрируема (в собственном или несобственном смысле) от a до b; тогда имеет место формула типа (7):
, причем эта производная (если ее значения в точках, где она не существует, выбрать произвольным образом) интегрируема (в собственном или несобственном смысле) от a до b; тогда имеет место формула типа (7):
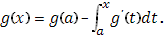
Если 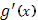 абсолютно интегрируема, то к функции
абсолютно интегрируема, то к функции  полностью приложимо изложенное в III.
полностью приложимо изложенное в III.
продолжение
