Проверка статистических гипотез

Статистической гипотезой называется любое предположение о виде или параметрах неизвестного распределения. Выдвинутую статистическую гипотезу, которую подвергают проверке, называют нулевой гипотезой и обозначают 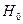. Каждая другая допустимая гипотеза, отличная от 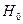, называется альтернативной и обозначается .

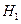В результате проверки гипотеза 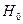принимается или отвергается, причём возможны четыре случая:

a) 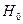верна, и её приняли; б) 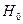верна, но ёё не отвергли;

в) 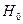неверна, но её приняли; г) 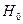неверна, и её отвергли.

Очевидно, что в случаях б) и в) принятое решение было ошибочным. Ошибка, совершённая в случае б), когда отвергается правильная гипотеза, называется ошибкой первого рода; совершённая в случае в), когда принята неверная гипотеза, называется ошибкой второго рода.

Предположим, что для контроля технологической операции производится измерение некоторого параметра. При нормальной работе станка (нулевая гипотеза 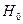) распределение контролируемого параметра не изменяется, если же произошла разладка станка (альтернативная гипотеза 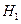), то характер распределения меняется. В этом случае ошибка первого рода - это пропуск бракованной продукции вследствие неправильно выбранного момента подналадки , а ошибка второго рода- это остановка для подналадки , когда станок работает нормально.

Вероятность совершить ошибку первого рода обозначают 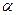и называют уровнем значимости или 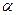-риском. Величина 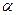обычно выбирается 0.05 (5%) или 0.01 (1%).

Вероятность совершить ошибку второго рода обозначают 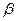и называют 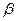-риском.

Однозначно определённый способ проверки статистических гипотез называется статистическим критерием. Обычно для проверки используют специальную случайную величину – статистику, распределение которой известно заранее. По данным выборок вычисляются частные значения входящей в критерий величины (статистики).

Совокупность значений статистики, при которой нулевая гипотеза отвергается , называется критической областью 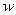, а множество значений статистики , при которой нулевая гипотеза принимается, образует область принятия гипотезы.

Обычно статистика 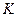- это случайная величина , принимающая действительные значения , поэтому критическая область и область принятия гипотезы- это интервалы числовой оси, отделяющиеся друг от друга критическими точками.

Величина критической области 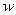определяется уровнем значимости 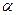. Вероятность попадания статистики в критическую область при условии, что справедлива альтернативная гипотеза 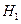(то есть 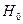будет отвергнута , если верна 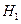), называется мощностью критерия. Очевидно, мощность равна 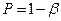. Мощность критерия – это вероятность не допустить ошибку второго рода.

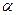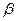При построении критической области стремятся уменьшить вероятности ошибок, однако при заданном объёме выборки невозможно уменьшить одновременно и и . Поэтому величины 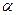и 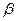выбирают в зависимости от « тяжести последствий» ошибок первого и второго рода для каждой конкретной задачи.

Принцип проверки статистической гипотезы не даёт логического доказательства её верности или неверности. Принятие гипотезы 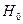означает только то, что эта гипотеза не противоречит имеющимся выборочным данным.

Для проверки гипотезы о виде теоретического закона распределения обычно применяют критерии согласия. При этом выдвигается гипотеза 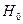о том, что исследуемая случайная величина 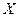подчиняется определенному закону распределения, и вычисляют статистику 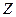меры расхождения теоретического (выбранного в гипотезе 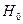) и эмпирического ( полученного по экспериментальным данным) распределения. Закон распределения 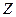должен быть известен , и тогда для выбранного уровня значимости 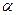легко установить 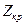. Если вычисленная величина 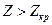, то гипотезу 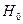отвергают, если 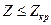, то гипотезу 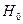принимают.

На практике наиболее часто применяют критерий согласия 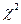- Пирсона. В этом критерии в качестве статистики 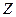берут 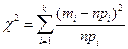, которая при 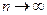имеет 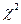- распределение с числом степеней свободы 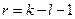, где 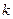-число интервалов эмпирического распределения ( интервальной таблицы частот), 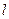- число параметров теоретического распределения.

Замечание. Необходимо, чтобы в каждом интервале было не менее 5 наблюдений ( 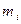>5) , если это не соблюдается, что следует объединить соседние интервалы.

Критические точки распределения 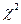приведены в Приложении 3.