Урок № 48. Тема 5.11. Вторая производная и ее физический смысл
Урок № 41. Тема 5.6. Производная сложной функции.
План.
1. Вывод формулы нахождения производной сложной функции.
2. Решение примеров.
Рассмотрим функцию
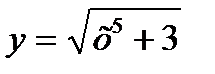 тогда
тогда
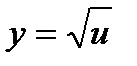 Возьмем еще функцию
Возьмем еще функцию
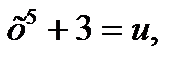
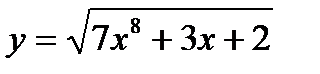
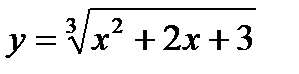
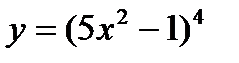
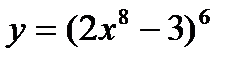
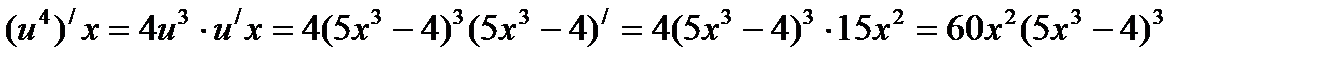
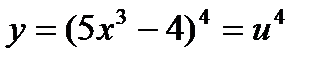
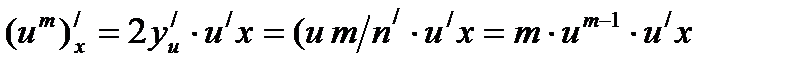
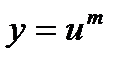
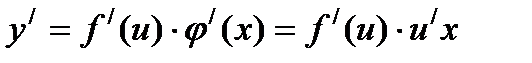
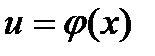
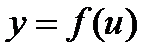 Обозначим тогда - сложная функция
Обозначим тогда - сложная функция
Пусть
Производная данной функции находится по формуле:
Рассмотрим сложную степенную функцию
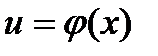
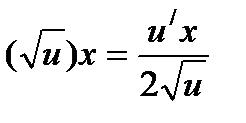
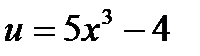 Рассмотрим
Рассмотрим
1)
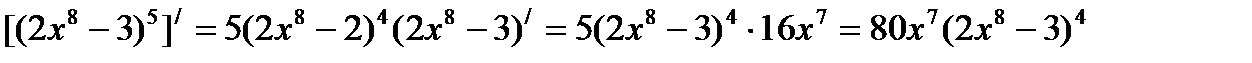
2)
u
Решить :
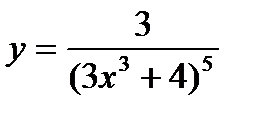
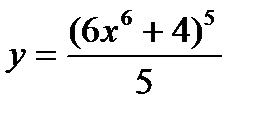
1) 2) 3)
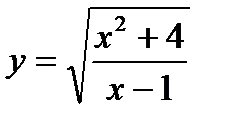
4) 5) 6)
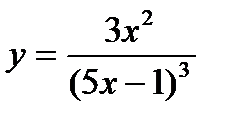
7)
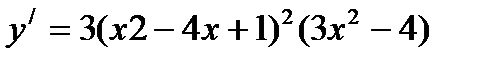
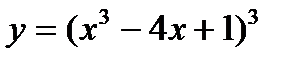 Домашнее задание
Домашнее задание
1)
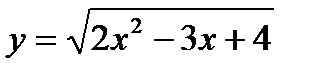
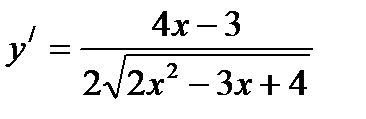
2)
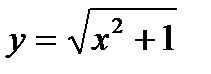
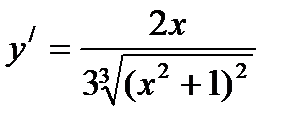
3)
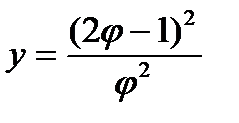
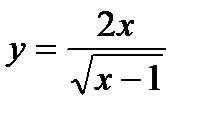
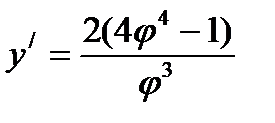
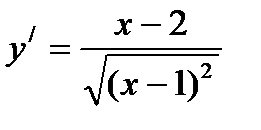
4)
5)
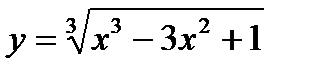
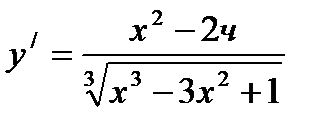
6)
Урок 43. Тема 5.7. Производная степенной функции с натуральным показателем. Производная синуса и косинуса.
План.
1. Производная степенной функции с натуральным показателем.
2. Производная тригонометрических функций.
Вывести формулы производных
у=С, у=х,…у=хn n – любое рациональное.
Найти производные функций
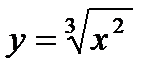
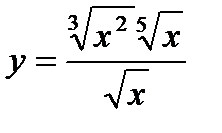
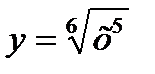
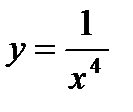
1) 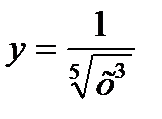 ; 2) 3) 4) 5)
; 2) 3) 4) 5)
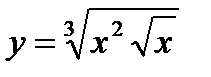
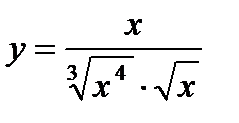 6) 7)
6) 7)
Найти производные функций
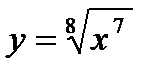
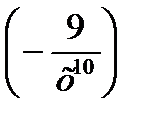
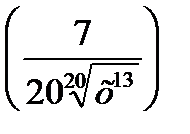
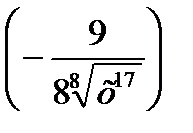
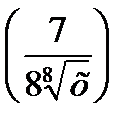
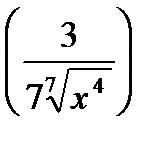 1) 2)
1) 2)
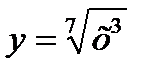
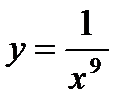
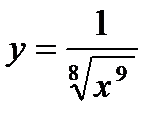
3) 4)
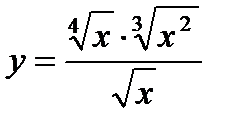
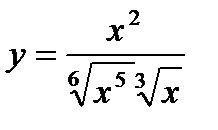
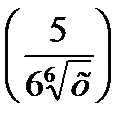
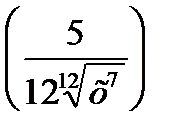
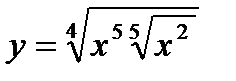 5) 6)
5) 6)
7)
Определение производной, последовательность нахождения ее.
Найти (sin x)/
1) 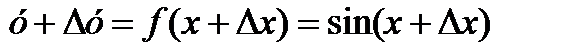
2) 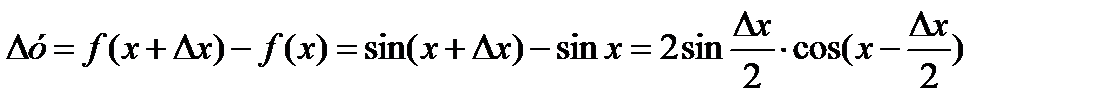
3) 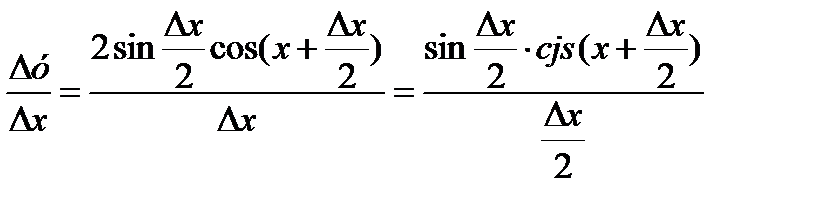
4) 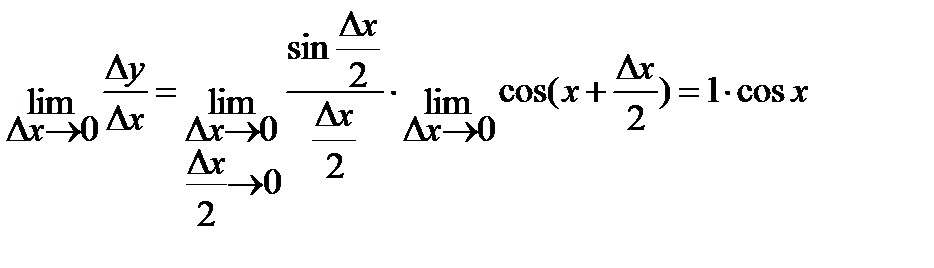
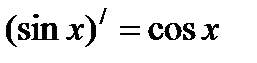
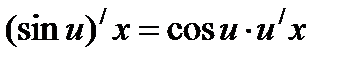
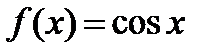
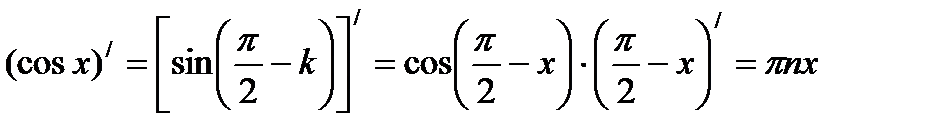
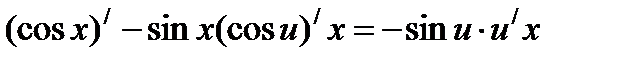
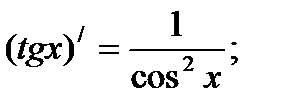
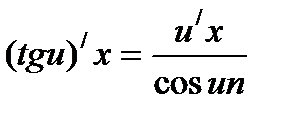
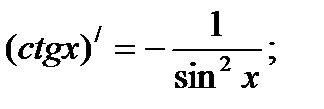
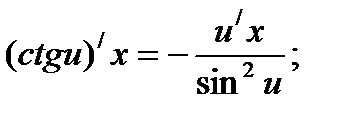
Решение упражнений:
Найти у/, если:
1. 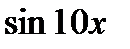 7.
7. 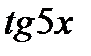 13.
13. 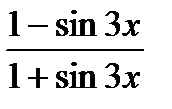
2. 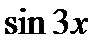 8.
8. 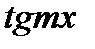 14.
14. 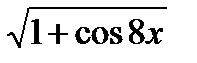
3. 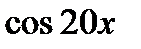 9.
9. 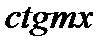 15.
15. 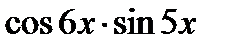
4. 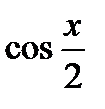 10.
10. 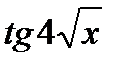 16.
16. 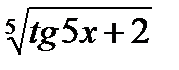
5. 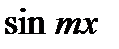 11.
11. 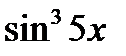
6. 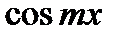 12.
12. 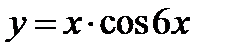
Контрольные вопросы:
1. Какая функция называется степенной?
2. По какой формуле находится производная степенной функции?
3. Какие тригонометрические функции вы знаете?
4. По какой формуле находится производная синуса и косинуса?
5. Нахождение производной называется?
Урок № 44. Тема 5.8. Производная показательной функции.
План.
Формулы нахождения производных показательной функции.
Решение упражнений.
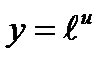
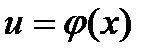
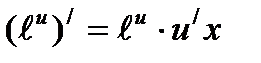
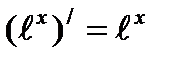
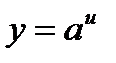
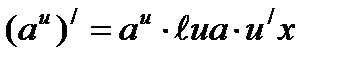
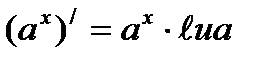
Найти производные функций
1) 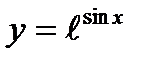 5)
5) 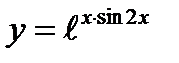 8)
8) 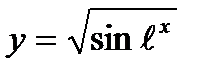
2) 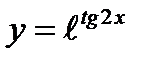 6)
6) 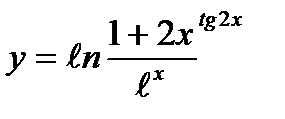 9)
9) 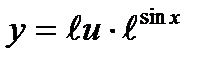
3) 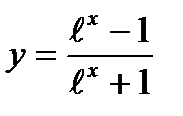 7)
7) 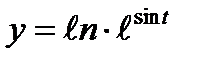
4) 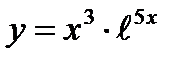
Домашнее задание
Найти у/, если:
1) 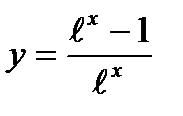
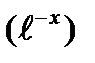
2) 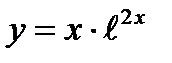
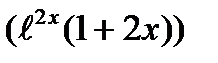
3) 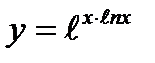
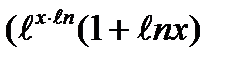
4) 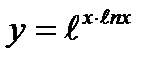
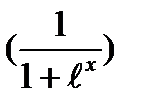
5) 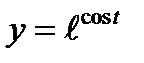
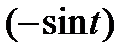
6) 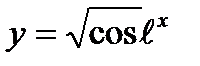
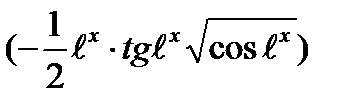
7) 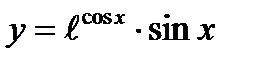
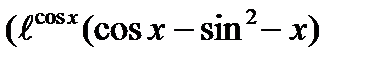
8) 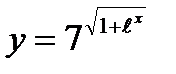
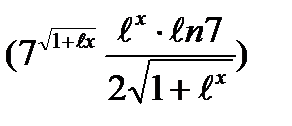
Урок № 45 .Тема 5.9. Производная логарифмических функций.
План.
1. Повторение определение логарифма, свойств.
2. Формулы нахождения производной логарифма.
3. Решение упражнений.
Рассмотрим предел вычисления 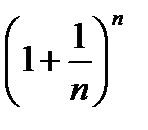 при n→∞. Предел
при n→∞. Предел 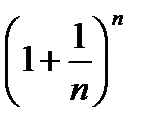 при n→∞ равный приближенно 2,718, принято обозначать буквой ℓ и это записывается
при n→∞ равный приближенно 2,718, принято обозначать буквой ℓ и это записывается
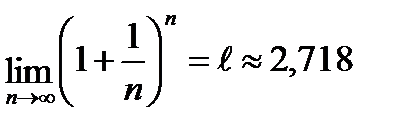
Определение: Логарифмы по основанию ℓ называются натуральными.
Натуральный логарифм числа N обозначается ℓnN. Между десятичным и натуральным логарифмами числа N существуют зависимости:
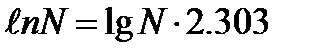
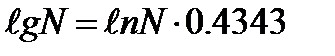
Рассмотрим формулы дифференцирования логарифмических функций
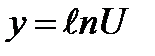
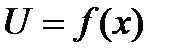
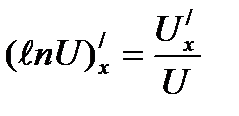
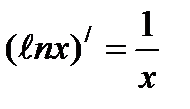
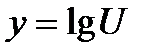
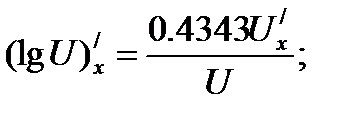
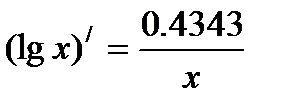
Решить примеры:
1) 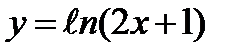 2)
2) 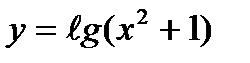
3) 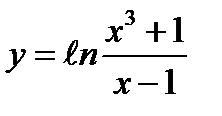 4)
4) 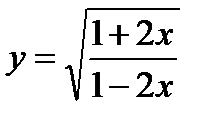
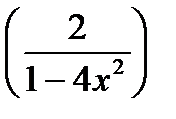
5) 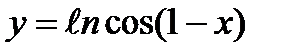 6)
6) 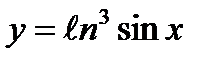 7)
7) 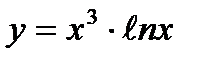
Домашнее задание
Найти у/, если:
1) 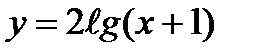
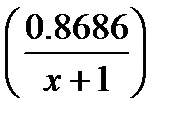
2) 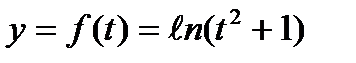
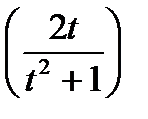
3) 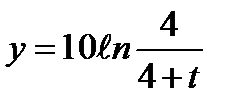
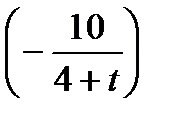
4) 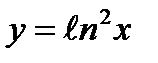
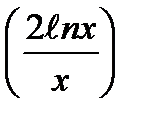
5) 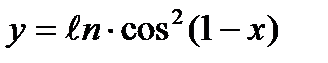
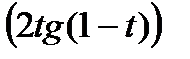
6) 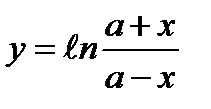
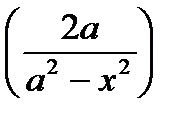
7) 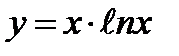
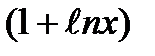
8) 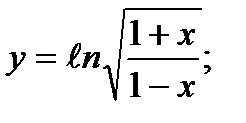
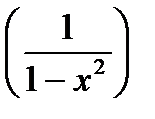
Контрольные вопросы:
1. Какая функция называется логарифмической функцией?
2. Какими свойствами обладает логарифмическая функция?
3. По какой формуле находится производная логарифмической функции?
4. По какой формуле находится производная натурального логарифма?
5. По какой формуле находится производная десятичного логарифма?
Урок № 46 (2) Тема 5.10. Производные обратных тригонометрических функций.
План.
1. Формулы нахождения производных обратно тригонометрических функций.
2. Решение упражнений
Формулы нахождения производных обратно тригонометрических функций.
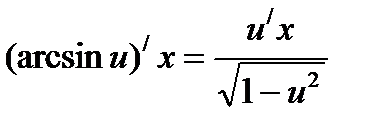
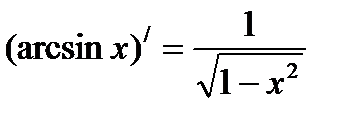
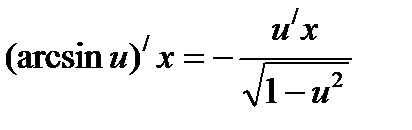
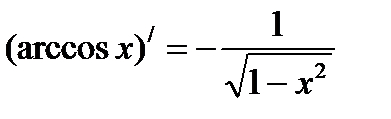
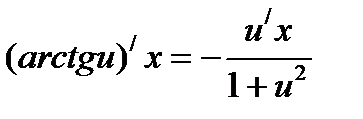
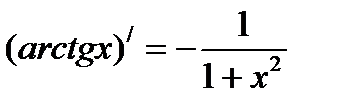
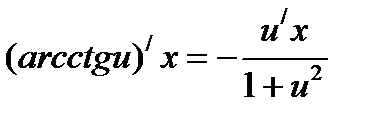
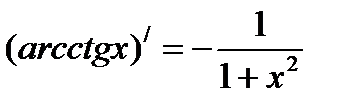
Решить упражнения:
1)  6)
6) 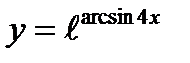
2) 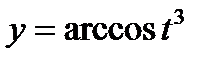 7)
7) 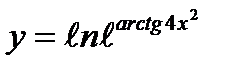
3) 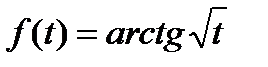 8)
8) 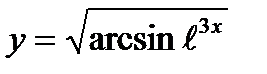
4) 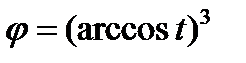 9)
9) 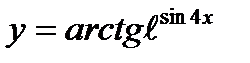
5) 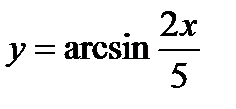
Домашнее задание
а) Повторить все формулы дифференцирования.
б) Найти у/, если:
1) 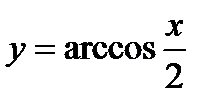
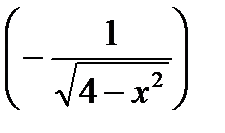
2) 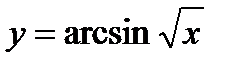
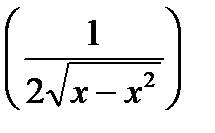
3) 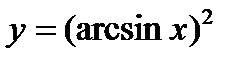
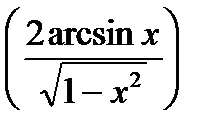
4) 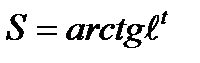
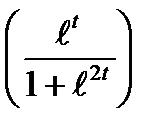
5) 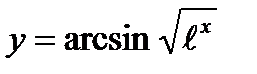
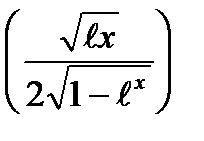
6) 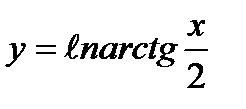
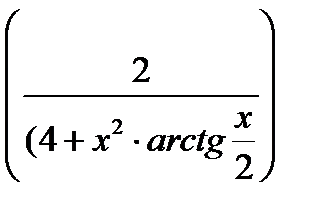
7) 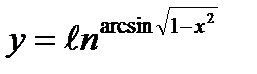
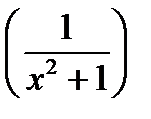
Урок № 48. Тема 5.11. Вторая производная и ее физический смысл.
План.
1.Определение второй производной функции.
2. Механический смысл производной II порядка.
Рассмотрим функцию 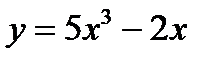
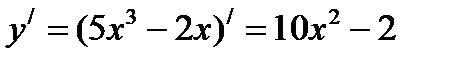 - I производная или производная нового порядка
- I производная или производная нового порядка
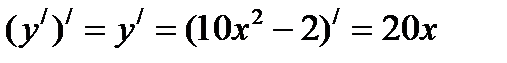 - II производная или производная второго порядка
- II производная или производная второго порядка
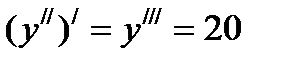 - III производная или производная третьего порядка
- III производная или производная третьего порядка
Определение:Производная от первой производной, если она существует, называется второй производной или производной II порядка.
Определение: Производная от второй производной, если она существует, называется третьей производной или производной III порядка.
Производная n порядка обозначается у(n)
