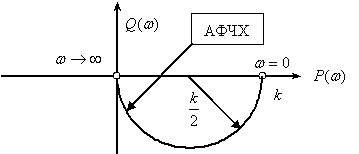Задания для самостоятельного решения№1
Временные характеристики
3.1.1 Определить реакцию на воздействие 1(t) объекта с передаточной функцией
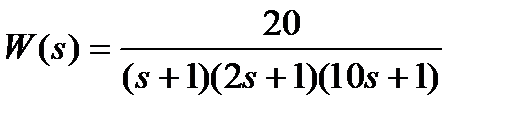 .
.
3.1.2 Записать изображение реакции на воздействие x(t) = t2, определить коэффициент передачи в установившемся режиме для объекта
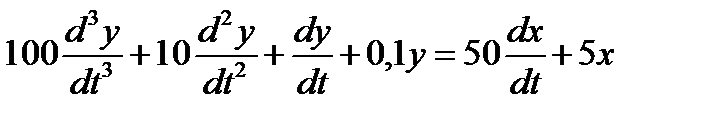 .
.
3.1.3 Система имеет коэффициент усиления k = 5, нуль –2 и полюса –1, –5 и –10. Определить реакцию на воздействие r(t) = d(t).
3.1.4 Найти реакцию системы (рисунок 3.7) на единичный скачок при нулевых начальных условиях
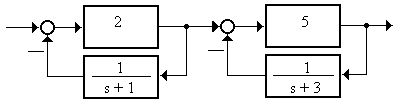
Рисунок 3.7
3.1.5 Найти с помощью преобразования Лапласа вынужденную составляющую переходного процесса от воздействия х(t) = t.
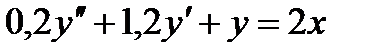
Задания для самостоятельного решения.
3.2.1 Записать изображение весовой функции системы с 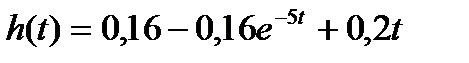 .
.
3.2.2 Вычислить h(t) системы (рисунок 3.8), если k = 9
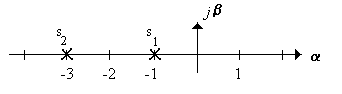
Рисунок 3.8
3.2.3 Весовая функция системы равна
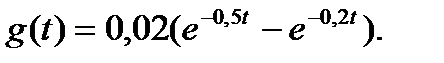
Записать изображение переходной функции.
3.2.4 Найти изображение весовой функции (рисунок 3.9)
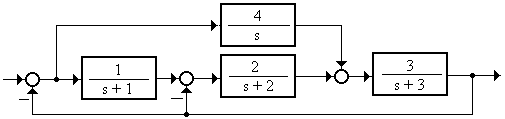
Рисунок 3.9
3.2.5 Записать h(t) фильтра по выходу а (рисунок 3.10)

Рисунок 3.10
при значениях параметров k1 = 1, k2 = 12, T1 = 1, T2 = 0,1.
3.2.6 Записать g(t) фильтра (рисунок 3.10) по выходу с при тех же значениях параметров схемы.
3.2.7 Найти оригинал передаточной функции объекта (рисунок 3.11)
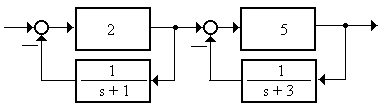
Рисунок 3.11
Задания для самостоятельного решения.
3.3.1 Описать свободное движение системы (рисунок 3.12) при начальных условиях y(0) = 1, y’(0) = -1.
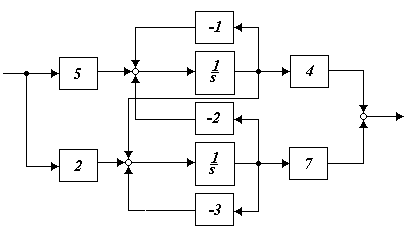
Рисунок 3.12
3.3.2 Решить с помощью преобразования Лапласа уравнение движения
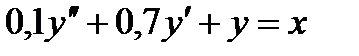 ,
,
если 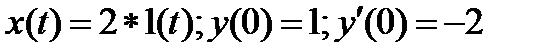 .
.
3.3.3 Найти реакцию системы (полюса равны –1, –2 и –3) на начальные условия 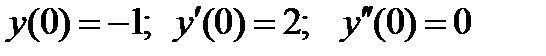 .
.
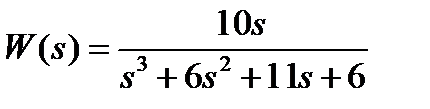 ,
,
3.3.4 Найти реакцию по выходу y (рисунок 3.13) на начальные условия y(0) = 0,5, y'(0) = 0,1 при значениях параметров k1 = 1, k2 = 1,2,
T1 = 3, T2 = 0,3.

Рисунок 3.13
3.3.5 Исследовать движение автономной системы при начальных условиях y(0) = 1, y’(0) = -1, если дано описание системы
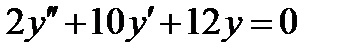 .
.
3.3.6 Каковы начальные условия, если изображение свободной составляющей переходного процесса равно
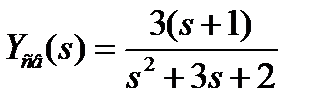 .
.
Задания для самостоятельного решения№2.
Частотные характеристики
3.1.1 Построить АФЧХ звена (рисунок 3.14), если k = 10
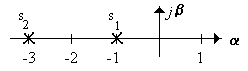
Рисунок 3.14
3.1.2 Записать формулы для вычисления АЧХ и ФЧХ системы (рисунок 3.18)
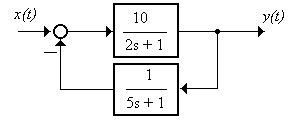
Рисунок 3.18
3.1.3 Записать формулы для вычисления АЧХ и ФЧХ системы (рисунок 3.19), если W1(s) = 10/(1 + 10s), W2(s) = 100/s, W3(s) = 1.
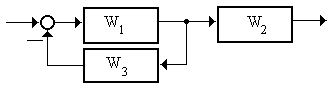
Рисунок 3.19
3.1.4 Записать дифференциальное уравнение движения для системы с комплексным коэффициентом передачи
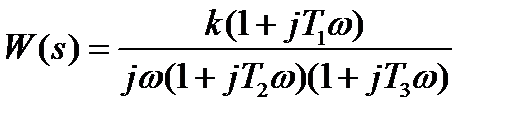 .
.
3.1.5 Построить АЧХ фильтра (рисунок 3.20) по выходу d

Рисунок 3.20
при значениях параметров k1 = 3, k2 = 4, T1 = 2, T2 = 0,1.
3.1.6 Описать формулой частотную реакцию y(t) на входное гармоническое воздействие x(t)=3sint, если передаточная функция фильтра равна
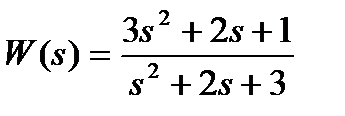 .
.
Методические указания к выполнению
Апериодическое звено
Передаточная функция
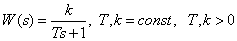 .
.
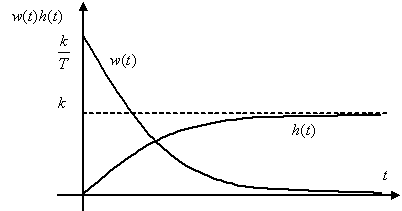
Временные характеристики
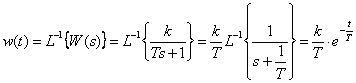 ,
,
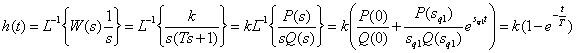 .
.
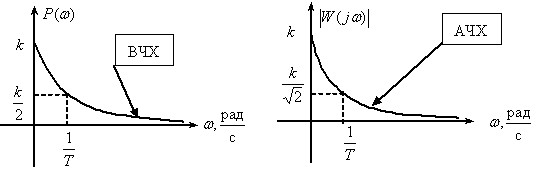
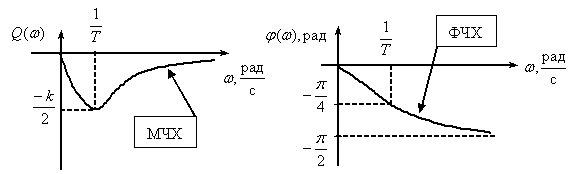
Частотная характеристика
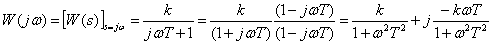 ,
,
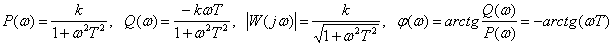 .
.