Механизм и его основные характеристики

Под механизмом, в широком смысле, понимается преобразователь механической энергии, подаваемой на его входы, в механическую энергию с требуемыми параметрами, получаемую на выходах. С этой точки зрения механизм, по принципу действия, аналогичен электрической схеме (которая преобразует электрическую энергию на входах в электрическую энергию, но с другими параметрами, на выходах схемы). В теории механизмов используется более конкретное определение:

механизм – система подвижно связанных между собой твердых тел, предназначенная для воспроизведения заданных движений одного или нескольких тел. По существу, это определение задает математическую модель, которая позволяет теоретически (с применением математики и теоретической механики) исследовать важнейшие свойства любого реального механизма.

Твердое тело, входящее в состав механизма, называется звеном.

Входным звеном называется то звено, посредством которого к механизму подводится механическая энергия от двигателя.

Выходным звеном механизма называется звено, совершающее требуемое технологическое движение.

Стойкой называется условно неподвижное (базовое) звено, относительно которого рассматривается движение остальных звеньев механизма.

У механизма может быть несколько входных и несколько выходных звеньев. Простейший случай – механизм с одним входным и одним выходным звеном.

Механизм может иметь множество различных характеристик (габаритные размеры, инерционные характеристики, упругая податливость кинематической цепи, максимальная передаваемая мощность, точность воспроизведения движений и т.п.), но к основным характеристикам любого механизма относят функцию положения и коэффициент полезного действия. Функция положения – это зависимость, связывающая положения выходных звеньев механизма с положениями его входных звеньев. Для механизма с одним входным и одним выходным звеном (рис. 1,а) функция положения записывается в виде:

,

где φ – положение входного звена, ψ – положение выходного звена.

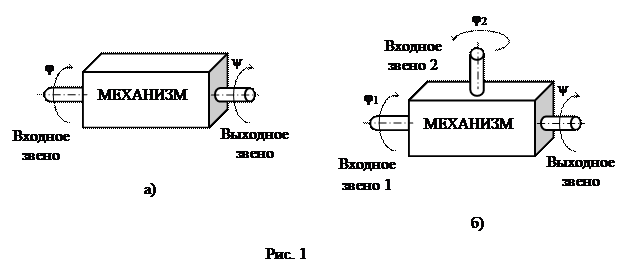В случае механизма с двумя входными и одним выходным звеном (рис. 1,б) функция положения будет функцией двух аргументов:

,

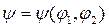где φ₁ – положение входного звена 1, φ₂ – положение входного звена 2. В общем случае у механизма может быть несколько функций положения:

, ,

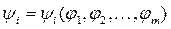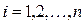где n – число выходных, m – число входных звеньев. Функция положения зависит от структурного строения механизма и от геометрических параметров его звеньев, но она явным образом не зависит от времени.

В некоторых задачах кинематики механизмов функция положения является заранее заданной, но в большинстве случаев она неизвестна и ее требуется определить.

Зная функцию положения, можно решать задачи кинематического, динамического, точностного анализа и синтеза механизма. Если требуется вычислить скорость 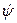и ускорение 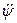выходного звена механизма (рис. 1,а), то это можно осуществить, воспользовавшись соотношениями:

,

,

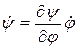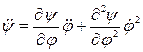где 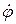- скорость, 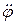- ускорение входного звена. Множитель 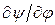называется первой передаточной функцией или аналогом скорости; множитель 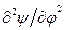- второй передаточной функцией или аналогом ускорения.

Задача

Передаточная функция кулачкового механизма с вращательным выходным звеном - коромыслом имеет вид 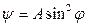, где φ, рад – угол поворота кулачка, ψ, рад – угол поворота коромысла, A – константа, определяемая геометрией механизма. Кулачок вращается по закону 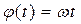, где ω, рад/c – постоянная угловая скорость кулачка. Найти угловую скорость и ускорение коромысла.

Решение

Так как кулачок вращается равномерно, то 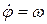и 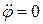. Вычислим аналог скорости и аналог ускорения:

, .

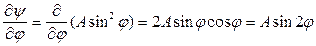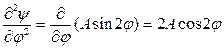Вычислим теперь скорость и ускорение коромысла, учитывая, что :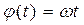

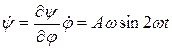, рад/c;

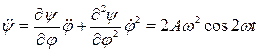, рад/с².

Коэффициент полезного действия представляет собой отношение полезной работы, совершаемой на выходных звеньях механизма, к работе, совершаемой двигателями на входных звеньях. КПД показывает, насколько эффективно данный механизм преобразует энергию. Уравнение баланса мощности, передаваемой механизмом, имеет вид:

,

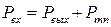где P_вх – мощность на входных звеньях механизма, P_вых – мощность на выходных звеньях механизма, P_тп – мощность тепловых потерь на трение. Поделив правую и левую части этого уравнения на P_вх, получим:

,

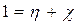где 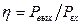- КПД, 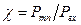- коэффициент потерь. Так как в любом реальном механизме есть потери мощности из-за наличия трения ( 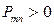), то его КПД находится в пределах 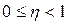. С точки зрения преобразования энергии механизм тем лучше, чем выше его КПД. Поэтому при проектировании, производстве и эксплуатации механизмов стремятся обеспечить значение КПД как можно более высоким. КПД механизма зависит от его конструктивного устройства, технического состояния, условий эксплуатации, наличия смазки, а также от полезной нагрузки на выходных звеньях. Зависимость КПД от мощности P, потребляемой на выходе механизма представлена графиком (рис. 2).

График показывает, что если механизм не нагружен (работает вхолостую), то его КПД равен нулю. Наибольшее значение КПД достигается при оптимальной нагрузке. Если механизм перегрузить, то его КПД, как показывает практический опыт, будет несколько меньше максимально возможного значения. Зависимость КПД механизмов от нагрузки следует учитывать при эксплуатации машин.

Контрольные вопросы

1. Дайте определение понятию «машина»

2. На какие категории подразделяются машины по функциональному назначению?

3. Из каких функциональных частей состоит машина?

4. В чем состоит прикладное значение теории механизмов и машин?

5. Дайте определение понятию «механизм»

6. Какие характеристики механизма являются основными?

7. Что такое функция положения механизма?

8. Почему функция положения механизма явно не зависит от времени?

9. Что называют аналогом скорости и аналогом ускорения?

10. Какие инженерные задачи могут быть решены с помощью функции положения механизма?

11. Что такое коэффициент полезного действия механизма?

12. Что характеризует КПД?

13. Почему КПД реальных механизмов всегда меньше единицы?

14. Почему КПД работающего вхолостую механизма равен нулю?