Целочисленное программирование

В некоторых экономических задачах (например, при определении оптимального выпуска машин, агрегатов, размещения оборудования) переменные характеризуют физически неделимые единицы и поэтому должны принимать только целые значения.

Формулировка задачи целочисленного программирования: найти наибольшее значение функции

при ограничениях:

,

, х_j - целые, .

Если k=n, то задача полностью целочисленная.

Если k не равно n, то задача является частично целочисленной.

Методы решения задач линейного программирования не гарантируют целочисленности решения.

Иногда задачи целочисленного программирования решают приближенно. Отбросив условие целочисленности, решают задачу методом линейного программирования, затем в полученном оптимальном решении округляют переменные до целых чисел. Такой прием можно использовать, если значения переменных достаточно велики и погрешностью округления можно пренебречь. Если значения переменных невелики, то округление может привести к значительному расхождению с оптимальным решением. Существует аналитический метод решения полностью целочисленных задач - метод Гомори.

Метод Гомори

Основная идея решения целочисленных задач, первоначально предложенная Данцигом, Фулкерсоном и Джонсоном, заключается в том, что задача сначала решается без ограничения целочисленности. Если решение получается целочисленным, то задача решена, если нет, то к задаче присоединяют новое дополнительное ограничение, которое называют сечением. Получают новую задачу, для которой множество допустимых решений будет меньше, чем для исходной задачи, но будет содержать все допустимые целочисленные решения.

Дополнительное ограничение отсекает часть области, содержащую нецелочисленное оптимальное решение.

Вновь полученную задачу решают методом линейного программирования. Процесс построения сечений и решения задачи повторяется до получения целочисленного оптимального решения. Общий систематический способ построения сечений разработал Гомори в 1958 г.

Алгоритм метода Гомори

Пусть дана полностью целочисленная задача линейного программирования: найти максимальное значение функции

при ограничениях:

,

, х_j - целые, .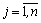

1) Отбросив условие целочисленности, решаем исходную задачу симплексным методом. Если получится целочисленное оптимальное решение, то задача решена. Если в оптимальном решении не все переменные целочисленны, то строим сечения.

2) Пусть в оптимальном решении переменная x_t - дробное число, т.е. x_t=f_t. Рассмотрим уравнение, в котором x_t - базисная переменная.

, (1)

где J - множество индексов свободных переменных.

Разобьем все коэффициенты и свободный член (1) на два слагаемых: целую и дробную часть. Целой частью числа а называется наибольшее целое число, не превышающее а. Дробной частью числа а называется разность между числом а и его целой частью. Целую часть числа обозначим [а], а дробную часть – {а}, т.е. а = [а]+{а}. Тогда уравнение (1) примет вид

, (2)

или

.

Для любого целочисленного решения задачи левая часть уравнения (2) есть целое число, следовательно, и правая часть также будет целым числом.

Неравенство

(3)

является сечением Гомори.

Покажем, что любое целочисленное решение задачи удовлетворяет этому неравенству, а нецелочисленное решение ему не удовлетворяет. Пусть - целочисленное решение, и предположим, что оно не удовлетворяет неравенству (3), т.е.

, или

по условию l_j > 0, , отсюда , кроме того, . Получим

, или , т.е. является дробным числом.

Подставив в уравнение (2), получим

.

Правая часть уравнения - дробное число, а левая часть - целое число. Получили противоречие. Следовательно, любое целочисленное решение задачи удовлетворяет неравенству (3).

Покажем, что нецелочисленное оптимальное решение не удовлетворяет неравенству (3).

Пусть - нецелочисленное оптимальное решение задачи. Подставим его в неравенство (3):

, но

Следовательно, не удовлетворяет неравенству (3).

3) Присоединяя неравенство (3) к ранее решенной задаче, получим новую задачу линейного программирования, которую вновь решаем симплексным методом; если ее оптимальное решение окажется целочисленным, то оно и будет оптимальным решением исходной задачи. Если снова получится нецелочисленное решение, то строим новое сечение, и т.д.

Замечание. Если в оптимальном решении несколько переменных нецелочисленные, то сечение строят по базисной переменной, имеющей наибольшую дробную часть.

Пример. Найти наибольшее значение функции

при ограничениях:

х₁ > 0, х₂ > 0, х₁, х₂ - целые.

Решим задачу симплексным методом без учета целочисленности, для этого приведем ее к каноническому виду

х_j > 0, .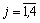

№ п/п	сj	Б.п.
x1	x2	x3	x4	bi
		x4 x5	2 -1	-1
Dj		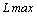-2	-2
		x1 x4		-1/2 3/2	1/2 1/2		7/2 13/2
Dj		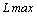	-3
		x1 x2			2/3 1/3	1/3 2/3	17/3 13/3
Dj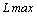

max L = 20.

Решение нецелочисленное, поэтому строим сечение Гомори. Возьмем первое уравнение из последней симплексной таблицы, так как у х₁ наибольшая дробная часть .

.

Сечение примет вид или

, где х₅>0.

Присоединив это дополнительное ограничение к ограничениям последней симплексной таблицы, получим новую задачу:

Решим эту задачу симплексным методом.

№ п/п	сj	Б.п.
x1	x2	x3	x4	х5	bi
		х1 x2			2/3 1/3 2/3	1/3 2/3 1/3	-1	17/3 13/3 2/3
		x1 x2 х3				1/2 1/2	1/2 -3/2
Dj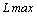

max L = 18.

Это решение целочисленное, значит исходная задача решена.

max L = 18, .

Дадим геометрическую иллюстрацию метода Гомори. Областью допустимых решений является четырехугольник ОАВС. Оптимальное решение задачи совпадает с точкой .

Построили сечение х₁ < 5, оно отсекает нецелочисленное оптимальное решение. Получили область допустимых решений ОАDЕС. Оптимально решение второй задачи будет в точке D (5, 4). Решение получилось целочисленным, следовательно, исходная задача решена.