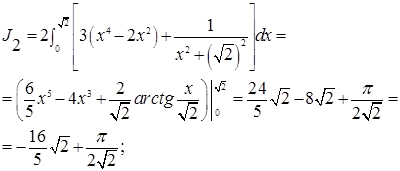Нтегрирование по частям в определенном интеграле

Для определенных интегралов имеет место формула интегрирования по частям, аналогичная той, которая была получена для неопределенного интеграла

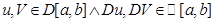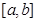Пусть на имеем: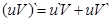

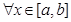
По формуле Н-Л 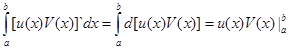и кроме того

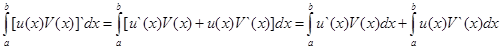
Откуда 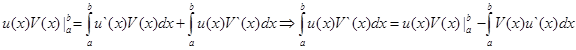или 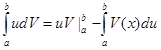ч.т.д.

а обобщенная формула интегрирования по частям перейдет в такую:

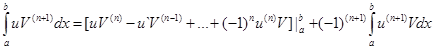
При этом по прежнему функции и все встречающиеся производные предполагаются непрерывными.

ример 1.

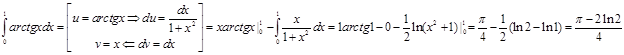
Пример 2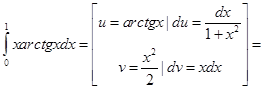

Замена переменного под знаком определенного интеграла

Пусть требуется вычислить 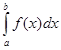от . Иногда, как в неопределенном интеграле бывает удобно произвести замену перестановкой «х» на новую переменную t, которые связаны между собой соотношением:

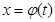
Докажем относительно такой замены теорему

Th2. Пусть выполнены следующие условия:

1. Уравнения 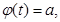и 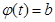имеют решения

(Обозначим их соотвественно 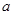и 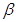, так что , )

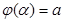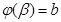2. Функция 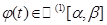(имеет непрерывную производную 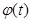на )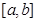

3. При изменении 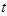на отрезке 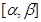значение функции 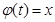не выходит из отрезка 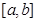(т.е 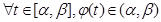) и следовательно сложная функция 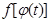определена 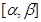(или ).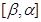

Тогда имеет место равенство:

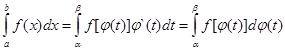(1)

Называемое формулой замены переменной под знаком определенного интеграла

Доказательство

Пусть

на 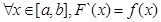, тогда по формуле Ньютона-Лейбница имеем 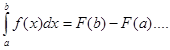(2), рассмотрим на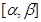 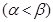функцию 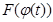переменного t определенную соотношением 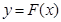и 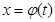. Вычислим ее производному по правилу сложной функции:

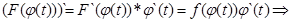что функция 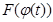является первообразной для функции 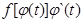на сегменте .

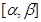Тогда по формуле Ньютона-Лейбница (которая здесь применима, т.к. функция 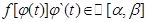) имеем:

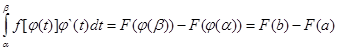(3)

(т.к. по условию )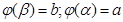

Сопоставляя равенства (2) и (3) мы и получим доказываемую формулу (1)

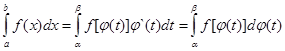(1) ч.т.д

амечание.

При использовании формулы (1) ф-ю 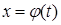следует стараться выбрать так, чтобы новый интеграл был более простым для вычисления, чем первоначальный.

Пределы 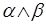нового интеграла определяются из уравнени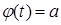й: и 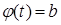. При этом эти уравнения могут иметь по несколько корней, тогда за 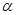можно принять любой корень уравнения 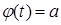, а за 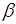любой корень уравнения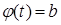

Лишь бы выполнялись условия 2 и 3 th. Условие th3 окажется, в частности, наверняка выполненным, если ф-я 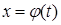будет монотонной на [a,b]

Поэтому на практике замену переменного осуществляют с помощью монотонных функций.

Если ф-я 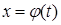не может принимать значений, равных пределам интегрирования a и b, то она не может служить для выполнения замены переменного в этом интеграле.

нтегрирование четных и нечетных функций.

Th Пусть 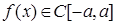на симметричном относительно начала координат сегменте.

Тогда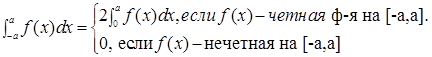

Док-во

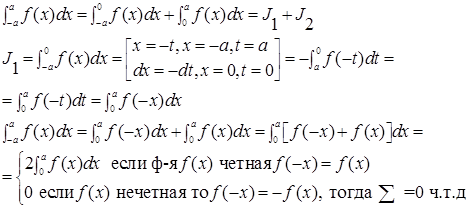
ример 1.

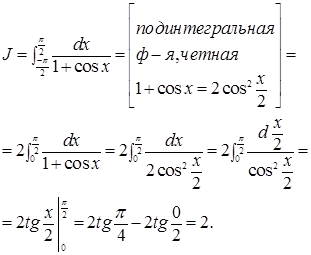
Пример 2.

Решение. Ф-я 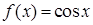четна. Докажем, что ф-я 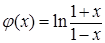нечетна;

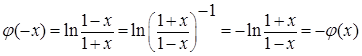
Т.О., подынтегральная ф-я представляет собой произведение четной и нечетной функции, т.е является 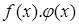– нечетная ф-я, поэтому J=0

Замечание. Если ф-я f(x) периодическая с периодом Т то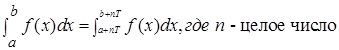

Пример 3.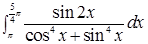

Решение. Подынтегральная ф-я является периодической с периодом Т= , т.к

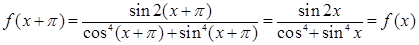
Поэтому от верхнего и нижнего пределов интегрирования можно отнять число π:

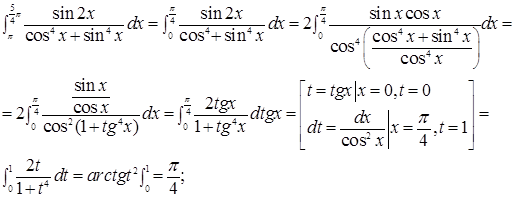
Пример 4. Вычислить интеграл.

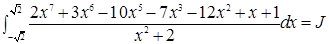
Решение.

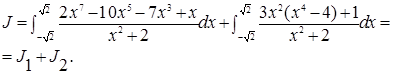
Мы разложили ин-л J в сумму двух интегралов Т.О., чтобы под знаком первого ин-ла стояла нечетная ф-я, а под знаком второго интеграла – четная функция. Тогда 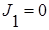.