Интегрирование рациональных дробей

Первообразная или неопределенный интеграл

Определение первообразной

Определение. Функция называется первообразной функции на отрезке , если для всех точек этого интервала выполняется равенство .

Теорема 1. Если и две первообразные функции , то разность между ними равна постоянному числу.

Доказательство:

Рассмотрим новую функцию , равную разности первообразных функции . Нетрудно видеть, что , а значит .

Следствие. Если для некоторой функции найдена какая-нибудь первообразная , то любая другая первообразная имеет вид .

Определение. Если есть первообразная функции , то выражение называется неопределенным интегралом и обозначается .

– подынтегральная функция; – подынтегральное выражение.

.

Теорема 2. Если функция непрерывна на отрезке , то для этой функции существует первообразная на этом отрезке.

Свойства неопределенного интеграла

1. Производная от неопределенного интеграла равна подынтегральной функции .

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению

.

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная. .

4. .

5. .

6. Если , то

а) ,

б) ,

в) .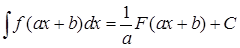

Таблица интегралов

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. .

Методы интегрирования

Интегрирование методом подстановки

Заметим, что следующие равенства не зависят от того, как обозначается переменная или

или .

Пусть любая дифференцируемая функция. Тогда , что следует из правила дифференцирования сложной функции .

Часто метод подстановки применяется в другой форме. В этом случае переменную представляют как функцию вспомогательного аргумента .

Интегрирование по частям

Пусть и функции, имеющие непрерывные производные. Тогда . Интегрируя это равенство, получим . Для получения формулы осталось выразить из правой части.

– формула интегрирования по частям.

Интегрирование рациональных дробей

Напомним, что корнем многочлена называется число (действительное или комплексное), такое, что . При этом многочлен можно разложить на множители , где – кратность корня . Если , то корень называется простым. В случае если многочлен с действительными коэффициентами имеет комплексный корень, то комплексное число, сопряженное данному корню, также является корнем этого многочлена. Тогда в разложении многочлена на множители входит квадратный трехчлен с отрицательным дискриминантом .

Дробно-рациональной функцией называется функция вида , где и многочлены соответственно степени . Если , то дробь называется правильной. В противном случае – неправильной. Для неправильной дроби нужно выполнить процедуру выделения целой части, то есть представить данную неправильную дробь как сумму многочлена и правильной дроби . Где – частное и остаток от деления числителя дроби на знаменатель соответственно.

.

Для того чтобы проинтегрировать правильную дробь ее нужно разложить в сумму простейших дробей. К простейшим дробям относятся такие дроби: . Разложение дроби в сумму простейших определяется следующими правилами.

а) Знаменатель имеет простые действительные корни

Теорема 1. Пусть простой корень знаменателя дроби . Тогда данную правильную дробь можно представить в виде суммы двух других правильных дробей .

б) Знаменатель имеет действительные кратные корни

Теорема 2. Пусть – корень знаменателя дроби кратности , тогда данную правильную дробь можно представить в виде суммы двух других правильных дробей .

Следствие.

в) Знаменатель имеет комплексные корни

Теорема 3. Пусть два комплексных сопряженных числа являются корнями знаменателя дроби . Тогда данную правильную дробь можно представить в виде суммы двух других правильных дробей .