Первый закон термодинамики для потока
На рис. 6.1 показан участок трубы, по которой движется газообразное рабочее тело.
В сечении 1-1 скорость и другие параметры потока равны c1, p1, t1, h1,..., в сечении 2-2 соответственно c2, p2, t2, h2,..., q, Дж/кг- теплота, подводимая к рабочему телу или отводимая от него, lT , Дж/кг- техническая работа, совершаемая самим потоком или над ним.
Первый закон термодинамики, имеющий вид
  |
выполняется и для потока рабочего тела. При этом внешняя работа потока представляет собой сумму изменения его кинетической и потенциальной энергий, а также технической работы
 , |
где g = 9,81 м/с2 - ускорение силы тяжести.
Таким образом, первый закон термодинамики для потока рабочего тела имеет вид
 , Дж/кг. | (6.1) |
Для сопел и диффузоров (коротких каналов с высокой скоростью течения рабочего тела) выполняются условия:
 , |
поэтому (6.1) принимает вид
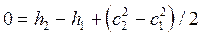 . | (6.2) |
В дифференциальной форме это равенство записывается так:
 . | (6.3) |
Связь изменения скорости и параметров состояния в потоке
Сравнение различных форм записи первого закона термодинамики:
 |
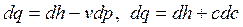дает следующее уравнение:
 . | (6.4) |
Из структуры (6.4) следует, что dc и dp всегда имеют противоположные знаки, т.е. при увеличении скорости (dc >0) давление в потоке уменьшается (dp < 0). Торможение потока (dc <0) всегда сопровождается возрастанием давления (dp >0).
В адиабатном потоке на основании (6.3) имеем
 , | (6.5) |
т.е. с увеличением скорости (dc > 0) энтальпия потока уменьшается (dh < 0), и наоборот.
Изменение энтальпии в адиабатном потоке прямо пропорционально изменению температуры и внутренней энергии, изменение давления - обратно пропорционально изменению удельного объема.
Таким образом, при увеличении скорости адиабатного потока рабочего тела (dc > 0):
1) p, T, h, u – уменьшаются;
2) удельный объем v увеличивается;
3) энтропия в обратимых процессах не изменяется (s = const), в необратимых процессах она увеличивается (ds >0).
 |  | ||
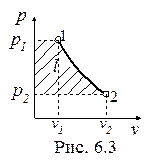На рис. 6.2 и 6.3 в T-s- и p-v- диаграммах показан адиабатный процесс истечения газа из сопла (dc > 0).
Параметры торможения
При торможении (остановке) потока (c2 = 0) удельный объем уменьшается до v0, давление, температура, энтальпия возрастают до значений p0, T0, h0, называемых параметрами торможения.
Подстановка c2 = 0, h2 = h0 в (6.2) дает формулу для расчета энтальпии торможения
 . | (6.6) |
Определение остальных параметров торможения (p0, T0, v0) зависит от вида используемого рабочего тела (водяной пар или идеальный газ).
Параметры торможения потока водяного пара с характеристиками p1, t1, скоростью c1 определяются с помощью диаграммы либо по таблицам воды и водяного пара. При этом энтальпию (h0) рассчитывают по уравнению (6.6).
Принимая процесс торможения (1-0) адиабатным, параметры p0, T0, v0 находят в точке пересечения s1 и h0 (точка 0, рис.6.4).
Для идеального газа на основании (6.6) можно записать
 . | (6.7) |
Подставляя 
в (6.7), получаем
 . | (6.8) |
Давление и объем в состоянии торможения рассчитываются по уравнениям:
 , | (6.9) |
 . | (6.10) |
Скорость звука
Импульс давления (упругие колебания) распространяется в сжимаемой среде со скоростью звука, равной
 , | (6.11) |
где r, кг/м3 - плотность.
С учетом уравнения адиабатного процесса 
формула для вычисления скорости звука записывается так:
 . | (6.12) |
Для идеального газа с использованием уравнения состояния 
формула (6.12) принимает вид
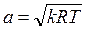 . | (6.13) |
Согласно (6.13) скорость звука зависит от свойств рабочего тела и от его температуры. С увеличением последней скорость звука растет.