Метод непосредственного применения законов Кирхгофа

На рис. 1.7 изображена схема разветвленной электрической цепи. Известны величины сопротивлений и ЭДС, необходимо определить токи.

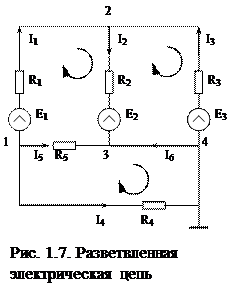В схеме имеются четыре узла, однако если составить четыре уравнения по первому закону Кирхгофа, то одно из них окажется линейно зависимым. Если в схеме имеется n узлов, то количество независимых уравнений, которые можно составить по первому закону Кирхгофа, равно n - 1. Для схемы на рис. 1.5 число независимых уравнений равно трем.

Выберем произвольно направления токов. Запишем уравнения.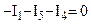

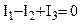(1.11)

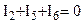
Недостающее количество уравнений составляют по второму закону Кирхгофа. Уравнения по второму закону составляют для независимых контуров.

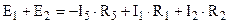
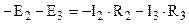(1.12)

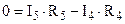
Независимым является контур, в который входит хотя бы одна новая ветвь, не вошедшая в другие контуры. Выберем три независимых контура и укажем направления обхода контуров. Запишем три уравнения по второму закону Кирхгофа. Решив совместно данные системы уравнений, определим токи в схеме.

Ток в ветви может иметь отрицательное значение. Это означает, что действительное направление тока противоположно выбранному.

Метод контурных токов

Метод непосредственного применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество совместно решаемых уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа.

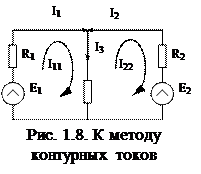Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах. На рис. 1.8 в качестве примера изображена двухконтурная схема, в которой I₁₁ и I₂₂ - контурные токи.

Токи в сопротивлениях R₁ и R₂ равны соответствующим контурным токам. Ток в сопротивлении R₃, являющийся общим для обоих контуров, равен разности контурных токов I₁₁ и I₂₂, так как эти токи направлены в ветви с R₃ встречно.

Порядок расчета.

Выбираются независимые контуры, и задаются произвольные направления контурных токов. В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:

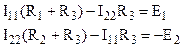
Решая уравнения, определим контурные токи I₁₁ и I₂₂, затем от контурных токов переходим к токам в ветвях.

Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви. В схеме на Рис.1.8

.I₁=I₁₁; I₂=I₂₂; I₃=I₁₁ - I₂₂.

Рекомендации

1) Контуры выбирают произвольно, но целесообразно выбрать контуры таким образом, чтобы их внутренняя область не пересекалась ни с одной ветвью, принадлежащей другим контурам.

2) Контурные токи желательно направлять одинаково (по часовой стрелке или против).

3) Если нужно определить ток в одной ветви сложной схемы, необходимо сделать его контурным.

4) Если в схеме имеется ветвь с известным контурным током, этот ток следует сделать контурным, благодаря чему количество уравнений становится на единицу меньше.