Сердечно-сосудистой системы человека
ЧЕТЫРЕХКАМЕРНАЯ МОДЕЛЬ
Ключевые слова и фразы:гемодинамика; математическая модель; сердечно-сосудистая система.
Аннотация:Представлено математическое описание четырехкамерной модели сердечно-сосудистой системы с пульсирующим сердцем. Сердечно-сосудистая система представляется в виде последовательно соединенных четырех упругих камер.
Список обозначений: 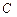 – эластичность камеры, см3/торр;;
– эластичность камеры, см3/торр;; 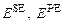 – коэффициент, характеризующий упругие свойства элементов миокарда, торр;
– коэффициент, характеризующий упругие свойства элементов миокарда, торр; 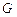 – геометрическая константа;
– геометрическая константа; 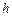 – средняя толщина стенки камеры сердца, см;
– средняя толщина стенки камеры сердца, см; 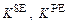 – коэффициент, характеризующий упругие свойства элементов миокарда;
– коэффициент, характеризующий упругие свойства элементов миокарда; 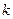 – насосный коэффициент;
– насосный коэффициент; 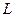 – инерционность потока крови, торр× с2/см3;
– инерционность потока крови, торр× с2/см3; 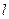 – длина элемента, см;
– длина элемента, см; 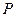 – давление в камере, торр;
– давление в камере, торр; 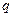 – объемный кровоток, см3/с;
– объемный кровоток, см3/с; 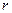 – радиус камеры, см;
– радиус камеры, см; 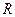 – гидравлическое сопротивление, торр×с/см; s – доля сократительных нитей в площади поперечного сечения миокарда;
– гидравлическое сопротивление, торр×с/см; s – доля сократительных нитей в площади поперечного сечения миокарда; 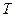 – период сердечных сокращений, с;
– период сердечных сокращений, с; 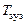 – длительность систолы, с; t – время, с;
– длительность систолы, с; t – время, с; 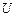 – ненапряженный объем, см3; u – систолический тонус сердечной камеры, см3;
– ненапряженный объем, см3; u – систолический тонус сердечной камеры, см3; 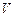 – объем i-й камеры, см3;
– объем i-й камеры, см3; 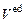 – конечный диастолический объем, см3;
– конечный диастолический объем, см3; 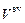 – ударный объем, см3; b – константа, характеризующая проводимость клапана сердца при регургитации, см–3; D – объем регургитации, см3;
– ударный объем, см3; b – константа, характеризующая проводимость клапана сердца при регургитации, см–3; D – объем регургитации, см3; 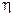 – коэффициент, характеризующий вязкость миокарда, торр×с; e – относительная линейная деформация; r – проводимость, см/торр . с;
– коэффициент, характеризующий вязкость миокарда, торр×с; e – относительная линейная деформация; r – проводимость, см/торр . с; 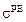 – напряжение в параллельном упругом элементе, торр;
– напряжение в параллельном упругом элементе, торр; 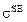 – напряжение в последовательном упругом элементе, торр;
– напряжение в последовательном упругом элементе, торр; 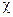 – коэффициент сокращения, с-1; подстрочный индекс: i – обозначение i-й камеры модели.
– коэффициент сокращения, с-1; подстрочный индекс: i – обозначение i-й камеры модели.
Для диагностики и терапии кардиологических больных ведется разработка программно-аппаратных комплексов [1], основу которых составляют математические модели сердечно-сосудистой системы (ССС).
Предлагается математическая модель ССС, состоящая из четырех последовательно соединенных элементов: LH – левое сердце (Left Heart);
SC – большой круг кровообращения (Systemic Circulation); RH – правое сердце (Right Heart); PC – малый круг кровообращения (Pulmonary Circulation) (рис. 1). В состав элементов ССС входят последовательно соединенные камеры и клапаны. Допущения модели ССС принимаются такими же, как в работе [2].
В модели CCC каждая i-я камера (рис. 2) характеризуется соответственно функциями объемного кровотока, объема, давления: qi (t), Vi (t), Pi (t),
i 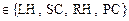 .
.
Изменение объема крови Vi (t)в i-й камере равно разности притока в камеру qi–1(t)и оттока из камеры qi (t). Уравнения баланса крови в камерах модели в дифференциальной форме выглядят следующим образом [2]:
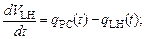 (1)
(1)
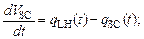 (2)
(2)
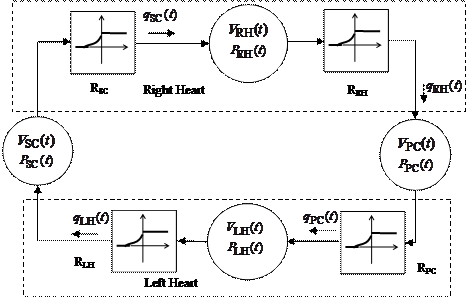
Рис. 1. Камерная структура модели кровообращения
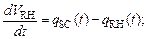 (3)
(3)
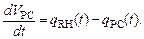 (4)
(4)
При моделировании динамических процессов в камерах большого и малого кругов кровообращения следует учитывать инерционные свойства кровотока и гидравлическое сопротивление. Для камер правого и левого сердца инерционность можно не учитывать, так как основную роль играет гидравлическое сопротивление. Уравнения движения для кровотока записываются в виде [2]:
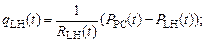 (5)
(5)
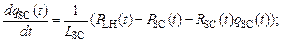 (6)
(6)
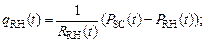 (7)
(7)
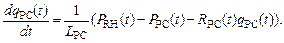 (8)
(8)
Сопротивления Ri, 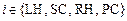 , определяются состоянием клапанов сердца. Открытие клапана происходит в момент, когда возникает сколь угодно малый перепад давлений кровотока в направлении открытия. Клапан остается полностью открытым пока сохраняется перепад давления кровотока в направлении открытия и, следовательно, направление кровотока положительное. Закрытие клапана обусловлено перемещением (регургитацией) некоторого объема крови Di поступившего через клапан в направлении, противоположном его нормальной пропускной способности, для
, определяются состоянием клапанов сердца. Открытие клапана происходит в момент, когда возникает сколь угодно малый перепад давлений кровотока в направлении открытия. Клапан остается полностью открытым пока сохраняется перепад давления кровотока в направлении открытия и, следовательно, направление кровотока положительное. Закрытие клапана обусловлено перемещением (регургитацией) некоторого объема крови Di поступившего через клапан в направлении, противоположном его нормальной пропускной способности, для 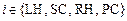 [3]:
[3]:
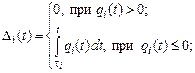 (9)
(9)
где 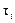 – начало периода времени, в котором кровоток qi имеет отрицательное направление.
– начало периода времени, в котором кровоток qi имеет отрицательное направление.
С увеличением объема регургитации величина сопротивления обратному току будет увеличиваться от величины 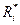 . Здесь
. Здесь 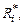
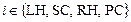 – гидравлическое сопротивление соответствующих камер. При наличии кровотока в обратном направлении проводимость
– гидравлическое сопротивление соответствующих камер. При наличии кровотока в обратном направлении проводимость
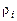 системы «камера – клапан» изменяется по закону [5], для
системы «камера – клапан» изменяется по закону [5], для 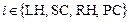
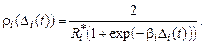 (10)
(10)
При достижении 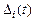 некоторой критической величины
некоторой критической величины 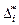 проводимость
проводимость 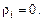
Переменное сопротивление в системе «камера – клапан» связано с проводимостью, для 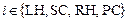
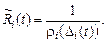 (11)
(11)
Тогда гидравлические сопротивления 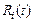 с учетом работы клапанов определяются как, для
с учетом работы клапанов определяются как, для 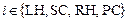
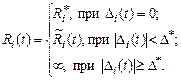 (12) (12)
(12) (12)
Зависимость функции давления Pi (t) для i 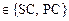 от функции объема Vi (t) записывается в виде уравнения Франка [3, 4]:
от функции объема Vi (t) записывается в виде уравнения Франка [3, 4]:
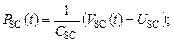 (13)
(13)
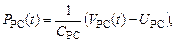 (14)
(14)
где USC, UPC– максимальный объем крови в камере, не вызывающий растяжения стенок (расправляющий или ненапряженный объем).
Для определения зависимости Pi (t)от Vi (t) для i  модель сердца рассматривается как двухкамерный резервуар. Для простоты предполагается, что каждая камера сердца – тонкостенная сфера.
модель сердца рассматривается как двухкамерный резервуар. Для простоты предполагается, что каждая камера сердца – тонкостенная сфера.
Связь давления в камере сердца с напряжением в стенке камеры и размерами камеры определяется законом Лапласа для тонкостенной сферы, 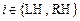 (рис. 3, а) [4, 5]:
(рис. 3, а) [4, 5]:
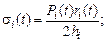 (15)
(15)
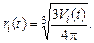 (16)
(16)
Из уравнений (15) – (16) следует:
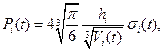
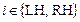 . (17)
. (17)
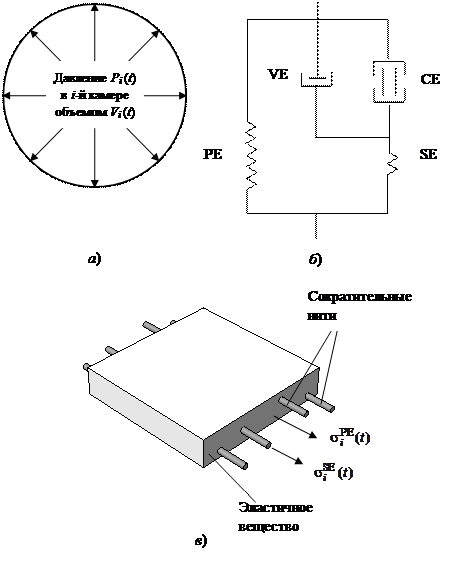
Рис. 3. Сердечная мышца (миокард):
а – представление сердечной камеры в виде тонкостенной сферы;
б – четырехэлементная реологическая модель миокарда;
в – пространственная модель миокарда
Для определения функции 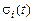 рассматривается модель сердечной мышцы.
рассматривается модель сердечной мышцы.
Принимается четырехэлементное представление сердечной мышцы (рис. 3, б). Стенка сферы (камеры) представляет собой сердечную мышцу (миокард).
Функциональная структура миокарда включает сократительный элемент CE, который способен укорачиваться при возбуждении, последовательно связанный с ним упругий элемент SE и параллельный упругий элемент PE. Для адекватного описания поведения миокарда в фазе расслабления, параллельно сократительному элементу включен вязкостный элемент VE.
Пространственный аналог одномерной четырехэлементной модели показан на рис. 3, в.
В пространственном аналоге параллельный упругий элемент PE представлен пассивным эластичным веществом, в которое погружены одномерные активные сократительные нити.
Напряжение 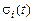 в миокарде выражается взвешенной суммой [5]:
в миокарде выражается взвешенной суммой [5]:
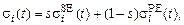
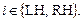 (18)
(18)
Напряжения в упругих элементах SE,PE i-й сердечной камеры определяются зависимостями [5]:
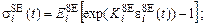 (19)
(19)
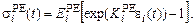 (20)
(20)
Из (17) – (20) следует, что давление в i-й сердечной камере равно
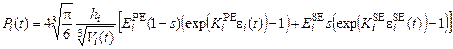 .
.
(21)
Переменные, характеризующие линейные размеры элементарной полоски миокарда, связаны с переменными Vi (t)и 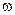 i (t)для
i (t)для 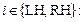
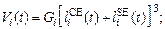 (22)
(22)
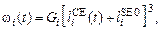 (23)
(23)
где 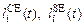 – текущие длины соответственно сократительного и последовательного упругого элемента;
– текущие длины соответственно сократительного и последовательного упругого элемента; 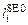 – начальная (ненапряженная) длина последовательного упругого элемента;
– начальная (ненапряженная) длина последовательного упругого элемента; 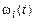 – вспомогательная переменная, представленная как объем псевдополости (псевдообъем) [4],
– вспомогательная переменная, представленная как объем псевдополости (псевдообъем) [4],
в котором последовательный упругий элемент имеет постоянную
длину 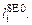
Пусть для 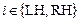
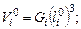 (24)
(24)
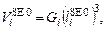 (25)
(25)
где 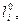
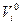 – длина элементарной полоски и объем миокарда в ненапряженном состоянии;
– длина элементарной полоски и объем миокарда в ненапряженном состоянии; 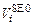 – объем полости, при условии, что она образована только из элементов постоянной длины
– объем полости, при условии, что она образована только из элементов постоянной длины 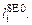
Тогда присутствующие в (21) относительные линейные деформации элементарной полоски миокарда 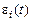 и последовательного упругого элемента
и последовательного упругого элемента 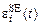 выражаются на основе (22) – (25) как
выражаются на основе (22) – (25) как
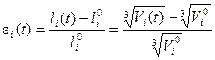 , (26)
, (26)
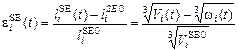 . (27)
. (27)
Таким образом, давление в сердечной камере в фазе расслабления и сокращения миокарда определяется уравнениями (21), (26), (27) в которых неизвестной остается функция 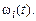
Для определения 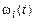 в фазе расслабления рассматривается скорость изменения относительной линейной деформации сократительного элемента
в фазе расслабления рассматривается скорость изменения относительной линейной деформации сократительного элемента 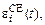 для которого справедливо уравнение [5]:
для которого справедливо уравнение [5]:
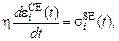
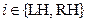 . (28)
. (28)
Уравнение (28) соответствует четырехэлементному представлению миокарда (рис. 3, б).
Так как длина  =
= 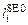 +
+ 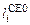 или
или 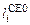 =
= 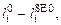 то с учетом (23), (25) для относительной линейной деформации сократительного элемента получается для
то с учетом (23), (25) для относительной линейной деформации сократительного элемента получается для 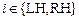
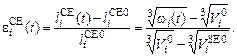 (29)
(29)
В результате дифференцирования (28) по t на основе (19), (29) получим формулу для фазы расслабления миокарда:
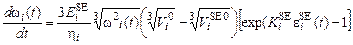 ,
, 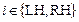 .
.
(30)
Таким образом, уравнения (21), (26), (27), (30) определяют давление в сердечных камерах в состоянии расслабления.
Для описания фазы сокращения сердца принимается гипотеза [4]:
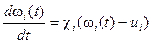 ,
, 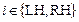 . (31)
. (31)
где 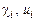 – константы, которые выбираются так, чтобы интегрально за сердечный цикл выполнялся закон Старлинга [5]. Линейная аппроксимация закона имеет вид [4],
– константы, которые выбираются так, чтобы интегрально за сердечный цикл выполнялся закон Старлинга [5]. Линейная аппроксимация закона имеет вид [4], 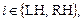
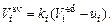 (32)
(32)
Общее решение дифференциального уравнения (31) имеет вид, 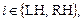
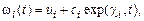 (33)
(33)
где 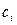 – произвольная постоянная общего решения (33) дифференциального уравнения (31).
– произвольная постоянная общего решения (33) дифференциального уравнения (31).
Тогда для выполнения закона Старлинга должны на основе (32), (33) выполняться зависимости, 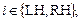
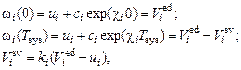 (34)
(34)
На основе решения системы (34) определяются коэффициенты 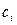 и
и 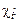
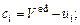 (35)
(35)
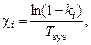
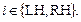 (36)
(36)
Таким образом, уравнения (21), (26), (27), (33), (35), (36) определяют давление в сердечных камерах в состоянии сокращения.
В модели пульсирующего сердца, деятельность сердца рассматривается как чередование фаз сокращения (систол) и фаз расслабления (диастол). Характеристиками этого процесса являются: период сердечных сокращение T и длительности систолы Tsys. Началом сердечного цикла является момент смены диастолы на систолу. В общем случае T и Tsys могут быть разными для разных циклов, тогда моменты окончания систолы tes(n) и окончания диастолы ted(n) n-го цикла, n = 1, 2, 3, …, выражаются формулами:
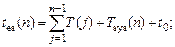 (37)
(37)
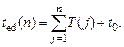
В течение всей систолы миокард подчинен уравнению (31) или (33), а в течение всей диастолы уравнению (30).
Переход от систолы к диастоле происходит путем смены этих уравнений.
Таким образом, замкнутая система уравнения (1) – (14), (21), (26), (27), (30), (33), (35) – (37) определяет четырехкамерную модель ССС человека, при решении которой определяются функции объемов 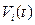 , давлений
, давлений 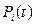 и объемных кровотоков
и объемных кровотоков 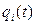 в каждой i-й камере,
в каждой i-й камере,  .
.
На основе четырехкамерной математической модели ССС разработана компьютерная программа на языке программирования С++.
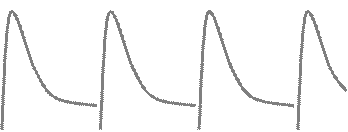
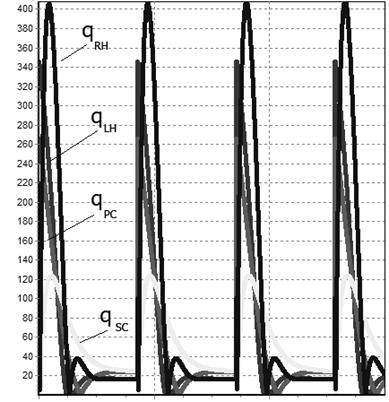
На рисунке 4 показаны в виде скриншота программы функции объемных кровотоков 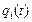 для параметров гемодинамики нормального человека [2].
для параметров гемодинамики нормального человека [2].
q, см3/с
|
|
|
|
| |
0 1 2 t, с
Рис. 4. Изменение кровотоков во времени в камерах модели LH, SC, RH, PC
Представленная модель является базовой моделью ССС. Предполагается дальнейшее развитие этой модели путем увеличения числа камер и более подробного описания элементов модели, например клапанов сердца.
Разработанная модель и усовершенствованные на ее основе модели ССС ориентированы для применения в интенсивной терапии. Кардиологическая интенсивная терапия имеет дело с острыми тяжелыми расстройствами кровообращения, где врач в прямом смысле берет в свои руки управление жизнедеятельностью организма в режиме on-line. Модель позволяет модифицировать и дополнить знания по клинической физиологии в соответствии с индивидуальной спецификой больного и исследовать их с ориентацией на диагностику и терапию [1]. Модель ССС рассчитана на применение в подсистемах поддержки принятия врачебных решений программно-аппаратных комплексов для операционных и палат интенсивной терапии кардиохирургических клиник. Это позволяет минимизировать время, затраченное специалистом на принятие решений и учесть при оценке ситуации и выборе терапии индивидуальные параметры пациента, сложность и специфику расстройств.
Программно-аппаратный комплекс делает возможным в режиме реального времени по данным мониторного контроля проводить детальный алгоритмический анализ и углубленную оценку состояния ССС, что позволит использовать комплекс при ведении тяжелых и осложненных больных с острыми нарушениями кровообращения во время кардиохирургических операций и в раннем послеоперационном периоде.
Закладываемые в программном обеспечении программно-аппаратного комплекса возможности имитации на модели кровообращения позволяют не в ущерб пациенту спрогнозировать предположительные состояния ССС в ответ на лечебные воздействия и манипуляции. Это дает возможность применять комплекс как для поддержки принятия решений при выборе и коррекции терапии, так и для обучения специалистов.
Список литературы
1. Стратегия информатизации медицины / В.А. Лищук [и др.]. – Ейск : ЮгПолиграф, 2011 – 248 с.
2. Модель сердечно-сосудистой системы, ориентированная на современную интенсивную терапию – 2008 / С.В. Фролов [и др.] // Вестн. Тамб. гос. техн. ун-та. – 2008. – Т. 14, № 4. – С. 892–902.
3. Лищук, В.А Система закономерностей кровообращения / В.А. Лищук // Клин. физиология кровообращения. – 2005. – № 4. – С. 14–24.
4. Лищук, В.А. Математическая теория кровообращения / В.А. Лищук. – М. : Медицина, 1991. – 256 с.
5. Лищук, В.А. Система закономерностей сердца / В.А. Лищук, Е.В. Мосткова // Клин. физиология кровообращения. – 2006. – № 1. – С. 16–21.
