Связность графа, деревья

Определение 1. Две вершины графа называются связными, если в графе существует путь с концами в этих вершинах, и несвязными в противном случае.

Определение 2. Граф называется связным, если любые две его вершины связны, и несвязным в противном случае.

Пример 1. Существует ли компания из шести человек, в которой каждый знаком с двумя, и только с двумя другими? Вариантов таких компаний может быть два.

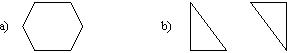
В первом случае мы имеем связный граф, во втором - несвязный.

Теорема 1. Связный граф G(X,T) представляет собой простой цикл тогда, и только тогда, когда каждая его вершина имеет степень 2.

Доказательство.

Необходимость. Пусть граф G(X,T) представляет собой простой цикл. Он является замкнутым простым путем. Из любой его вершины можно попасть в любую другую, не проходя ни через какую вершину два раза. Очевидно, что степень любой вершины такого графа равна 2.

Достаточность. Пусть граф G(X,T) связный и степень каждой его вершины равна 2. Любые две его вершины соединены путем. Возьмем произвольную вершину. Пойдем по одному из двух ребер, к которым принадлежит эта вершина. Мы попадем в следующую вершину, из которой выходит два ребра. По одному мы пришли. Двигаемся далее по второму ребру. Таким образом, все вершины графа будут пройдены и мы вернемся в исходную вершину. Путь замкнется. Следовательно, этот граф является циклом.

Определение 3. Ребро (x_i, x_j) называется мостом, если в графе G(X,T), полученном после удаления ребра (x_i, x_j), вершины x_i и x_j несвязны.

Пример 2.

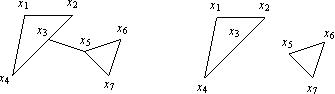
В исходном графе ребро (x₃, x₅) является мостом.

Существует несколько признаков мостов:

1) Ребро (x_i, x_j) является мостом тогда, и только тогда, когда (x_i, x_j) является единственным путем, соединяющим вершины x_i и x_j.

2) Ребро (x_i, x_j) является мостом тогда, и только тогда, когда найдутся две вершины x_k и x_m, такие, что любой путь, соединяющий их, содержит вершины x_i и x_j.

3) Ребро (x_i, x_j) является мостом тогда, и только тогда, когда оно не принадлежит ни одному циклу.

Определение 4. Связный граф без циклов называется деревом.

Определение 5. Вершина дерева, имеющая степень 1, называется висячей.

По аналогии с генеалогическими деревьями вводятся родовые понятия для вершин.

Пример 3.

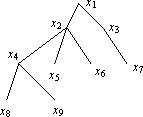
Вершина x₁ называется корневой, пути от нее называются ветвями. Вершина x₂ называется родительской по отношению к вершинам x₄, x₅, x₆ и прародительской по отношению к вершинам x₈, x₉. Вершины x₂ и x₃ называются дочерними к вершине x₁.

Пример 4. Кубок по настольному теннису разыгрывают 16 команд по олимпийской системе. Схему турнира можно изобразить деревом.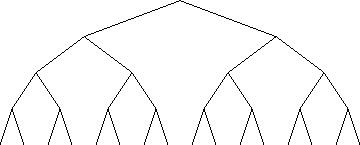

Любое ребро в дереве является мостом. Для каждой пары вершин дерева существует единственный соединяющий их путь.

Теорема 2. Дерево с n вершинами имеет n-1 ребро.

Изображение графа

Один и тот же граф может быть изображен по-разному.

Пример. На данных рисунках изображен один и тот же граф.

Для предварительной проверки совпадения графов необходимо проверить следующие условия:

1) одинаковое ли число вершин в графах;

2) одинаковое ли число ребер в графах;

3) одинаковое ли в графах число вершин имеют степень k .

Необходимым и достаточным условием совпадения графов является существование такого взаимно однозначного соответствия между ними, при котором две вершины в одном соединены ребром тогда, и только тогда, когда соединены ребром соответствующие вершины в другом.

Плоские графы

Определение 1. Граф G(X,T) называется плоским, если его можно изобразить на плоскости так, чтобы никакие два его ребра не имели других общих точек, кроме их общей вершины. Чертеж графа, на котором никакие два ребра не пересекаются, называют плоским представлением графа.

Примерами плоских графов могут служить простые циклы, деревья, лес и т.д.

Пример 1.Дан граф

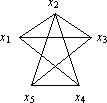
Его плоским представлением является граф

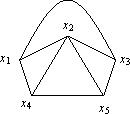
Плоское представление имеет только плоский граф, и обратно: у всякого плоского графа всегда найдется плоское представление.

Примером неплоского графа может служить полный граф с пятью вершинами.

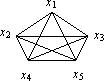
Любые попытки начертить его плоское представление обречены на неудачу.

Определение 2. Гранью в плоском представлении графа G(X,T) называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов.

Определение 3. Часть плоскости, расположенная вне плоского представления графа и ограниченная изнутри простым циклом, называется бесконечной гранью.

Определение 4. Две грани называются соседними, если их границы имеют хотя бы одно общее ребро.

Пример 2.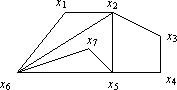

Данный граф имеет четыре обычные грани, ограниченные циклами (x₁, x₂, x₆, x₁), (x₅, x₆, x₇, x₅), (x₂, x₃, x₄, x₅, x₂), (x₂, x₅, x₇, x₆, x₂), и одну бесконечную грань, ограниченную циклом (x₁, x₂, x₃, x₄, x₅, x₆, x₁). Грани (x₁, x₂, x₆, x₁) и (x₂, x₅, x₇, x₆, x₂) являются соседними, а грани (x₁, x₂, x₆, x₁) и (x₂, x₃, x₄, x₅, x₂) соседними не являются. Часть плоскости, ограниченная простым циклом (x₂, x₅, x₆, x₂), не является гранью, так как содержит внутри себя цикл (x₅, x₆, x₇, x₅).

Пример 3.

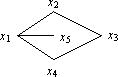
В данном графе часть плоскости, ограниченная простым циклом (x₁, x₂, x₃, x₄, x₁), является гранью, так как ребро (x₁, x₅), расположенное внутри грани, не является циклом.

Пример 4.

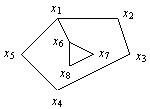
Часть плоскости, заключенная между циклами (x₁, x₂, x₃, x₄, x₅, x₁) и (x₆, x₇, x₈, x₆), не является гранью, так как она содержит внутри себя цикл и к тому же она не ограничена циклом. Ребро (x₁, x₆) является мостом, соединяющим два цикла.

Определение 5. Мост, соединяющий два цикла, называется перегородкой.

Пример 5.

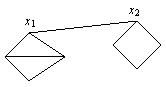
Данный граф не имеет бесконечной грани, так как она не ограничена изнутри простым циклом. Мост (x₁, x₂) является перегородкой.

В плоском представлении дерева за грань принимают всю плоскость чертежа.

Для всякого плоского графа без перегородок число вершин n, число ребер m и число граней с учетом бесконечной g связаны соотношением n - m + g = 2, которое называется формулой Эйлера.

Определение 6. Плоский граф G(X,T) называется максимально плоским, или триангулированным, если к нему невозможно добавить ни одного ребра так, чтобы полученный граф был плоским.

Пример 6. Рассмотрим граф

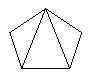
Данный граф можно сделать максимально плоским:

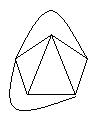
Каждая грань в плоском представлении максимально плоского графа имеет три вершины.

Определение 7. Операция добавления новых ребер, в результате которой в плоском представлении графа каждая грань имеет ровно три вершины, называется триангуляцией графа.

Теорема. Для любого плоского графа G(X,T) существует плоское представление, в котором все ребра - прямолинейные отрезки.

Эйлеровы графы

Определение 1. Эйлеровым путем в графе называется путь, содержащий все ребра графа и проходящий через каждое по одному разу.

Пример 1. Рассмотрим граф

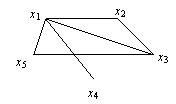
Он имеет эйлеров путь (x₄, x₁, x₃, x₂, x₁, x₅, x₃).

Определение 2. Эйлеровым циклом в графе называется цикл, содержащий все ребра графа и проходящий через каждое по одному разу.

Определение 3. Граф, обладающий эйлеровым циклом, называется эйлеровым графом.

Пример 2. Рассмотрим граф

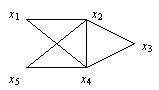
Данный граф является эйлеровым, так как он имеет эйлеров цикл (x₂, x₅, x₄, x₁, x₂, x₃, x₄, x₂).

Теорема 1. Эйлеров граф связный, и все его вершины четны.

Доказательство.

Связность следует из определения эйлерового графа. Эйлеров цикл содержит каждое ребро и притом только один раз. Следовательно, степень каждой вершины графа должна состоять из двух одинаковых слагаемых: количество входов в вершину и количество выходов из вершины.

Теорема 2. Если граф G(X,T) связный и все его вершины четны, то он обладает эйлеровым циклом.

Теорема 3. Если граф G(X,T) обладает эйлеровым путем с концами А и В, то граф G(X,T) связный и А и В его единственные нечетные вершины.

Доказательство.

Если путь начинается в А и кончается в В, то А и В нечетные вершины, даже если путь неоднократно проходил через них. В любую другую вершину путь должен привести и вывести из нее, т.е. остальные вершины четные.

Теорема 4. Если граф G(X,T) связный и А и В его единственные нечетные вершины, то граф обладает эйлеровым путем с концами А и В.

Теорема 5. Если граф G(X,T) связный, то можно построить цикличный маршрут, содержащий все ребра в точности 2 раза, по одному в каждом направлении.

Гамильтоновы графы

Определение 1. Гамильтоновым путем в графе называется путь, проходящий через каждую вершину графа в точности по одному разу.

Пример 1. Рассмотрим граф

Он имеет гамильтоновы пути (x₃, x₄, x₅, x₁, x₂) и (x₃, x₄, x₂, x₅, x₁).

Определение 2. Гамильтоновым циклом в графе называется цикл, проходящий через каждую вершину графа в точности по одному разу.

Определение 3. Граф, обладающий гамильтоновым циклом, называется гамильтоновым графом.

Пример 2. Рассмотрим граф

Данный граф является гамильтоновым, так как он имеет гамильтоновы циклы (x₁, x₇, x₆, x₃, x₄, x₅, x₂, x₁) и (x₁, x₆, x₃, x₄, x₅, x₂, x₇, x₁).

Всякий полный граф является гамильтоновым, так как он содержит такой простой цикл, которому принадлежат все вершины графа.

Теорема. Граф с m вершинами имеет гамильтонов цикл, если для любой его вершины A_i степень (A_i) > m/2.

Сети Петри

Сети Петри — математический аппарат для моделирования динамических дискретных систем. Впервые описаны Карлом Петри в 1962 году.

Сеть Петри представляет собой двудольный ориентированный граф, состоящий из вершин двух типов — позиций и переходов, соединённых между собой дугами, вершины одного типа не могут быть соединены непосредственно. В позициях могут размещаться метки (маркеры), способные перемещаться по сети.

Событием называют срабатывание перехода, при котором метки из входных позиций этого перехода перемещаются в выходные позиции. События происходят мгновенно, разновременно при выполнении некоторых условий.

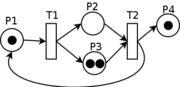
Пример сети Петри. Белыми кружками обозначены позиции, полосками — переходы, чёрными кружками — метки.