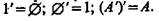Пересечение («умножение») классов

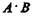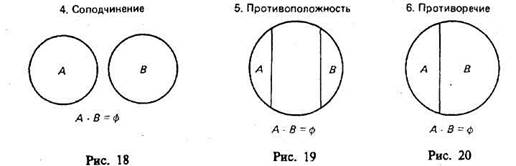
Общей частью, или пересечением, двух классов называется класс тех элементов, которые содержатся в обоих данных множе­ствах, т. е. это множество (класс) элементов, общих обоим мно­жествам¹⁸. Пересечение обозначается или 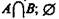— пустое множество. При пересечении могут встретиться следующие 6 слу­чаев (рис. 15—20, где результат пересечения заштрихован).

Например, операция пересечения классов «школьник» (А) и «футболист» (В) заключается в нахождении таких людей, кото­рые одновременно являются и школьниками, и футболистами. Это изображено на рис. 17, где общая часть классов А и В за­штрихована.

Основные законы логики классов. Законы операций объединения и пересечения

1. Законы идемпотентности.

А + А = А. А х А = А.

В школьном курсе алгебры таких законов нет. В логике первый из этих законов означает следующее. Если мы к классу «дом» прибавим класс «дом», то получим класс «дом», т. е. домов не станет в два раза больше и объем понятия «дом» останется прежним.

2. Законы коммутативности. Эти законы существуют в алгеб­ре, в арифметике, в теории множеств и в логике классов.

А + В = В+А. А В=В А.

Если мы к классу «растение» прибавим класс «животное», то получим класс «организм»; тот же самый класс получим, если мы к классу «животное» прибавим класс «растение».

3. Законы ассоциативности. Они существуют в арифметике, алгебре, теории множеств и в логике классов.

(А+В) + С = А + (В+С). (A х B) х C=A х (B х С).

4. Законы дистрибутивности.

(A+B)C=(A х С)+(B х С). (A х B) + C=(A + С) х (B+С).

5. Законы поглощения. Этих законов нет в арифметике и в школьном курсе алгебры.

А + (А х В)=А. А х (А+В)=А.

Доказательство этих законов осуществляется графическим методом. Два закона поглощения для «сложения» и «умножения» клас­сов иллюстрируются графически на рис. 21 и 22.

Промежуточный результат изображен горизонтальной штри­ховкой. В первом законе поглощения он равен А В, а во вто­ром — равен А + В. Конечный результат изображен вертикаль­ной штриховкой; он равен классу А.

Вычитание классов

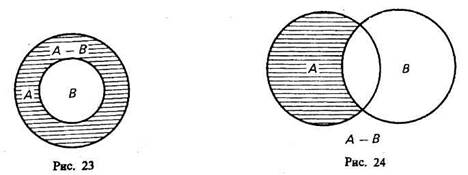
Рассмотрим два множества (класса) А и В, из которых В может и не быть частью А. Разностью множеств (классов) А и В на­зывается множество тех элементов класса А, которые не являют­ся элементами класса В. Разность обозначается А —В.

Могут встретиться следующие пять случаев (если классы А и В не пусты и не универсальны).

1-й случай (рис. 23). Класс А включает в себя класс В. Тогда разностью А — В будет заштрихованная часть А, т. е. множество тех элементов, которые не суть В. Например, если мы из множе­ства звуков русского языка (А) вычтем множество гласных звуков (В), то получим множество согласных звуков, изображенное на чертеже в виде заштрихованного кольца.

2-й случай (рис. 24). Разностью двух перекрещивающихся классов будет заштрихованная часть А. Например, разность мно­жеств «рабочий» (А) и «рационализатор» (В) даст множество рабочих, которые не являются рационализаторами.

3-й случай (рис. 25). Если класс А полностью включен в класс В и класс В полностью включен в класс А, то эти классы (множества) равны (тождественны). Тогда разность А -В даст пустой, или нулевой, класс, т. е. класс, в котором нет ни одного элемента. Например, если мы из класса «сосна» вычтем класс «сосна», то разность А—В будет равна пустому классу.

4-й случай (рис. 26). Класс А и класс В не имеют общих элементов.

Тогда разность А—В=А, так как всякий элемент класса А не является элементом класса В. Например, разность класса «стол» (А) и класса «стул» (В) равна классу «стол» (А).

В результате «вычитания» классов, соответствующих поняти­ям, находящимся в отношении противоположности [«низкий дом» (А), «высокий дом» (В)] или противоречия [«одушевленный предмет» (А), «неодушевленный предмет» (В)], разность А— В также равна А (рис. 27, 28).

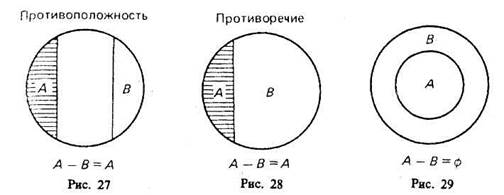
5-й случай (рис. 29). Если объем класса А меньше объема класса В, то в результате вычитания получим пустой класс, так как нет элементов класса А, которые не являлись бы элементами класса В. Например, разность класса «личное местоимение» (А) и «местоимение» (В) дает пустой класс.

Для операции вычитания классов справедливы следующие законы:

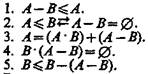
В интерпретации логических алгебр посредством классов за­пись 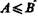обозначает включение класса А в класс В; 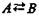обозна­чает эквивалентность классов (А тогда и только тогда, когда В ).

Дополнение к классу А

Дополнением к классу А называется класс А" который, будучи сложенным с А, дает рассматриваемую область предметов (эту область обозначим 1), а в пересечении с классом А дает 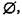т. е. для которого 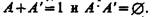Откуда А' = 1- А, поэтому

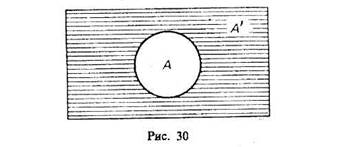
операцию дополнения к классу А можно рассматривать как частный случай операции «вычитания» (из универсального клас­са). Если от класса целых чисел (1) отнять класс четных чисел (А), то мы получим класс нечетных чисел (т. е. А" поскольку всякое целое число четное или нечетное и нет таких четных чисел, которые были бы нечетными). Графически это можно изобразить так, что заштрихованная часть будет обозначать дополнение к А, т. е. A' (рис. 30).

Для операции дополнения кроме указанных выше установ­лены и следующие законы: