Оценка сложных систем в условиях определенности

Теория систем основным объектом исследования, как правило, имеет сложные системы. Напомним, что под сложными понимаются системы, которые можно расчленить на конечное количество подсистем. Подсистемы в свою очередь могут быть разбиты на еще более мелкие подсистемы и т.д. до элементарных составляющих. Таким образом, любая сложная система имеет древовидную, иерархическую структуру. Все элементы сложных систем находятся во взаимодействии друг с другом (внутренняя среда) и с элементами и факторами внешней среды.

Результатом жизнедеятельности системы может быть совершенно определенный (детерминированный) исход. Так, например, изменения количества сотрудников детерминировано отразится на величине налогов, начисляемых на выплачиваемую заработную плату; увеличение НДС коррелирует с серыми схемами расчетов; продолжительный период морозов вызывает увеличение потребления энергоресурсов; наступление летнего сезона увеличивает спрос на вентиляторы и кондиционеры и т.п. Зависимости такого рода связаны с функциями системы или ее элементов, поэтому ее логично называют функциональной.

Определенность имеет место в большинстве математических задач, а также во многих моделях линейного и нелинейного программирования. Это могут быть модели поиска вариантов распределения ресурсов, дающих, наибольшую отдачу по определенному показателю (такому, как прибыль или стоимость), или наименьшему значению некоторого другого критерии (такого, как затраты) в условиях заданных ограничений.

Взаимодействия между объектами внутренней или внешней среды сложной системы, вызывающие определенные (детерминированные) последствия могут быть исследованы следующими методами системного анализа:

· методы математического программирования (например, метод теории поля, рассматривающий зависимость функций элементов от параметров сложной системы);

· методы структурного анализа сложных систем, позволяющие выделить в сложных системах подсистемы с их функциональными и количественными зависимостями;

· методы качественной теории сложных систем - исследование устойчивости систем.

Рассмотрим более подробно данные методы.

Многочисленная группа методов математического программирования исследователями обычно разбивается на несколько подгрупп-классов. Например, по характеру области допустимых значений и виду целевой функции эти методы можно разделить на следующие классы задач:

· линейного программирования – целевая функция и функция-ограничения имеют прямую зависимость, линейны;

· нелинейного программирования – зависимость целевой функции и функции-ограничения не имеют прямой, линейной зависимости.

По способу решения методы можно структурировать на : аналитические; графические; численные.

По другим критериям – на статические и динамические (по фактору времени), дискретные и непрерывные (по характеру процесса), одномерные и многомерные (по типу и количеству переменных) и т.д.

Задачи математическое программирование достаточно хорошо изучены и используется достаточно широко не только для информационно-аналитических систем, например, для разработки прикладных компьютерных программ системного анализа, но и для практических задач управления хозяйственно-экономических систем.

Приведем пример задачи производства и поставок, предлагаемой в качестве классического примера математического программирования в условиях определенности Г.И.Корниловым в «Основах теории систем и системного анализа»:

Пусть некоторая фирма должна производить и поставлять продукцию клиентам равномерными партиями в количестве N =24000 единиц в год. Срыв поставок недопустим, так как штраф за это можно считать бесконечно большим.Запускать в производство приходится сразу всю партию, таковы условия технологии. Стоимость хранения единицы продукции C_x=10 копеек в месяц, а стоимость запуска одной партии в производство (независимо от ее объема) составляет C_p =400 руб. Таким образом, запускать в год много партий явно невыгодно, но невыгодно и выпустить всего 2 партии в год — слишком велики затраты на хранение! Где же “золотая середина”, сколько партий в год лучше всего выпускать? Будем строить модельтакой системы. Обозначим через n размер партии и найдем количество партий за год — p = N / n 24000 / n. Получается, что интервал времени между партиями составляет t = 12 / p (месяцев), а средний запас изделий на складе — n/2 штук.Сколько же нам будет стоить выпуск партии в n штук за один раз? Сосчитать нетрудно — 0.1 · 12 · n / 2 руб. на складские расходы в год и 400 p руб. за запуск партий по n штук изделий в каждой.В общем виде годовые затраты составляютE = 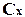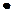T n / 2 + 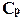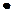N / n где T = 12 — полное время наблюдения в месяцах.Перед нами типичная вариационная задача: найти такое n₀, при котором сумма E достигает минимума. Решение этой задачи найти совсем просто — надо взять производную по n и приравнять эту производную нулю. Это даетn₀ = ,

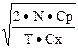что для нашего примера составляет 4000 единиц в одной партии и соответствует интервалу выпуска партий величиной в 2 месяца.

Затраты при этом минимальны и определяются как

E₀ = ,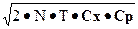

что для нашего примера составляет 4800 руб. в год.

С помощью алгоритмов линейного программирования решаются задачи управления запасами, распределения ресурсов. Кстати, первые задачи такого характера были исследованы еще задолго до появление собственно кибернетики и компьютерных технологий – в 1915 году. Это была задача минимизации затрат на заказ и хранение запасов при заданном спросе на продукцию и заданным уровнем цен. Основателем теоретического и практического исследования задач линейного программирования были положены Д.Данцингом и Л.В.Канторовичем. В 60-х годах XX века способы построения математических моделей сложных систем и методы их исследования выделились в самостоятельную научную дисциплину – теорию сложных систем.

В самом общем виде задача линейного программирования может быть представлена в следующем виде: требуется обеспечить минимум выражения (целевой функции)

E(X) = C1 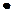X1 + C2 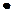X2 + ......+ Ci 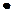Xi + ... Cn 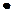Xn

при следующих условиях: все Xi положительны и, кроме того, на все Xi налагаются m ограничений (m < n)

A11·X1 + A12·X2 + ......+ Aij·Xj + ... A1n·Xn = B1;

.....................................................................................

Ai1·X1 + Ai2·X2 + ......+ Aij·Xj + ... Ain·Xn = Bi;

.....................................................................................

Am1·X1 + Am2·X2 + .....+ Amj·Xj+ ... Amn·Xn = Bm .

На практике только немногие ситуации могут оставаться определенными в достаточно длительном интервале времени. Поэтому, чаще всего мы встречаемся с ситуациями, имеющими два и более вероятностных исхода, т.е. с факторами неопределенности.