Система разностных уравнений, описывающих работу данной АСР, при переходном процессе

Так как рассчитываем переходный процесс по задающему воздействию, то полагаем DX_f = 0; DY_f = 0.

1. Уравнение объекта регулирования:

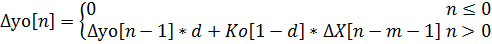
2.Уравнение датчика:

y₁ =K_{д *} y₀[n]

3.Уравнение элемента сравнения:К₂

ОШ[n]= y_заq[n] * K_д - y₁[n]

4.Уравнение регулирующего блока:

Выбираем параметры настройки ПИ регулятора:

K₁ = -2.2426

K₂ = -0.0147

Отклонение регулируемой величины от установившегося значения должно быть не более 5%. D = 0.05 × | 2 | = 0

Произведем ручной расчёт переходного процесса системы по задающему воздействию для 10 точек.Результаты занесем в таблицу 5.

Таблица 5

n	Y0	Y1	ОШ	Х = PE
			0.12	-0.35
			0.12	-0.46
			0.12	-0.57
			0.12	-0.68
			0.12	-0.8
			0.12	-0.91
	0.1925	0.011	0.109	-0.99
	0.43	0.026	0.094	-1.04
	0.7	0.042	0.078	-1.08
	1.004	0.06	0.6	-1.10
	1.34	0.08	0.4	-1.09

РЕЗУЛЬТАТЫ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ

ОДНОКОНТУРНОЙ ТИПОВОЙ НЕПРЕРЫВНОЙ АВТОМАТИЧЕСКОЙ СИСТЕМЫ

17.10.10

********************************************************************

ПЕРЕХОДНЫЙ ПРОЦЕСС ПО ЗАДАЮЩЕМУ ВОЗДЕЙСТВИЮ

Задающее воздействие ступенчатое = 2.0000

П И - З А К О Н РЕГУЛИРОВАНИЯ

Выбранные параметры закона :

Пропорциональная составляющая К1 = -2.2426

Интегральная составляющая К2 = -0.0147

Шаг расчета по времени = 20

Вывод производится через 2 тактов расчета

********************************************************************

Время Задание Ошибка Рег.у-во Система Ср.кв.ош.

0,00 2,00 0,1200 -0,3470 0,00000 4,00000

40,00 2,00 0,1200 -0,4380 0,00000 4,00000

80,00 2,00 0,1200 -0,5290 0,00000 4,00000

120,00 2,00 0,1080 -0,5852 0,20073 3,89106

160,00 2,00 0,0830 -0,5901 0,61725 3,52090

200,00 2,00 0,0570 -0,5729 1,05050 3,08672

240,00 2,00 0,0314 -0,5371 1,47700 2,67361

280,00 2,00 0,0102 -0,4955 1,82956 2,32663

320,00 2,00 -0,0059 -0,4532 2,09878 2,05352

360,00 2,00 -0,0167 -0,4151 2,27901 1,84355

400,00 2,00 -0,0227 -0,3838 2,37888 1,68026

440,00 2,00 -0,0247 -0,3602 2,41236 1,54860

480,00 2,00 -0,0238 -0, 3443 2,39611 1,43769

520,00 2,00 -0,0208 -0,3353 2,34688 1,34085

560,00 2,00 -0,0168 -0,3319 2,27955 1,25449

600,00 2,00 -0,0124 -0,3328 2,20629 1,17683

640,00 2,00 -0,0082 -0,3364 2,13606 1,10695

680,00 2,00 -0,0045 -0,3416 2,07476 1,04416

720,00 2,00 -0,0015 -0,3473 2,02560 0,98780

760,00 2,00 0,0006 -0,3528 1,98956 0,93715

800,00 2,00 0,0020 -0,3577 1,96604 0,89148

840,00 2,00 0,0028 -0,3616 1,95340 0,85010

880,00 2,00 0,0030 -0,3645 1,94944 0,81243

920,00 2,00 0,0029 -0,3663 1,95178 0,77796

960,00 2,00 0,0025 -0,3674 1,95820 0,74629

1000,00 2,00 0,0020 -0,3677 1,96676 0,71707

1040,00 2,00 0,0014 -0,3675 1,97593 0,69004

1080,00 2,00 0,0009 -0,3670 1,98460 0,66496

1120,00 2,00 0,0005 -0,3663 1,99206 0,64163

1160,00 2,00 0,0001 -0,3656 1,99795 0,61988

1200,00 2,00 -0,0001 -0,3649 2,00218 0,59956

На основании полученых данных построим график переходного процесса по каналу управления при изменение задающего воздействия.

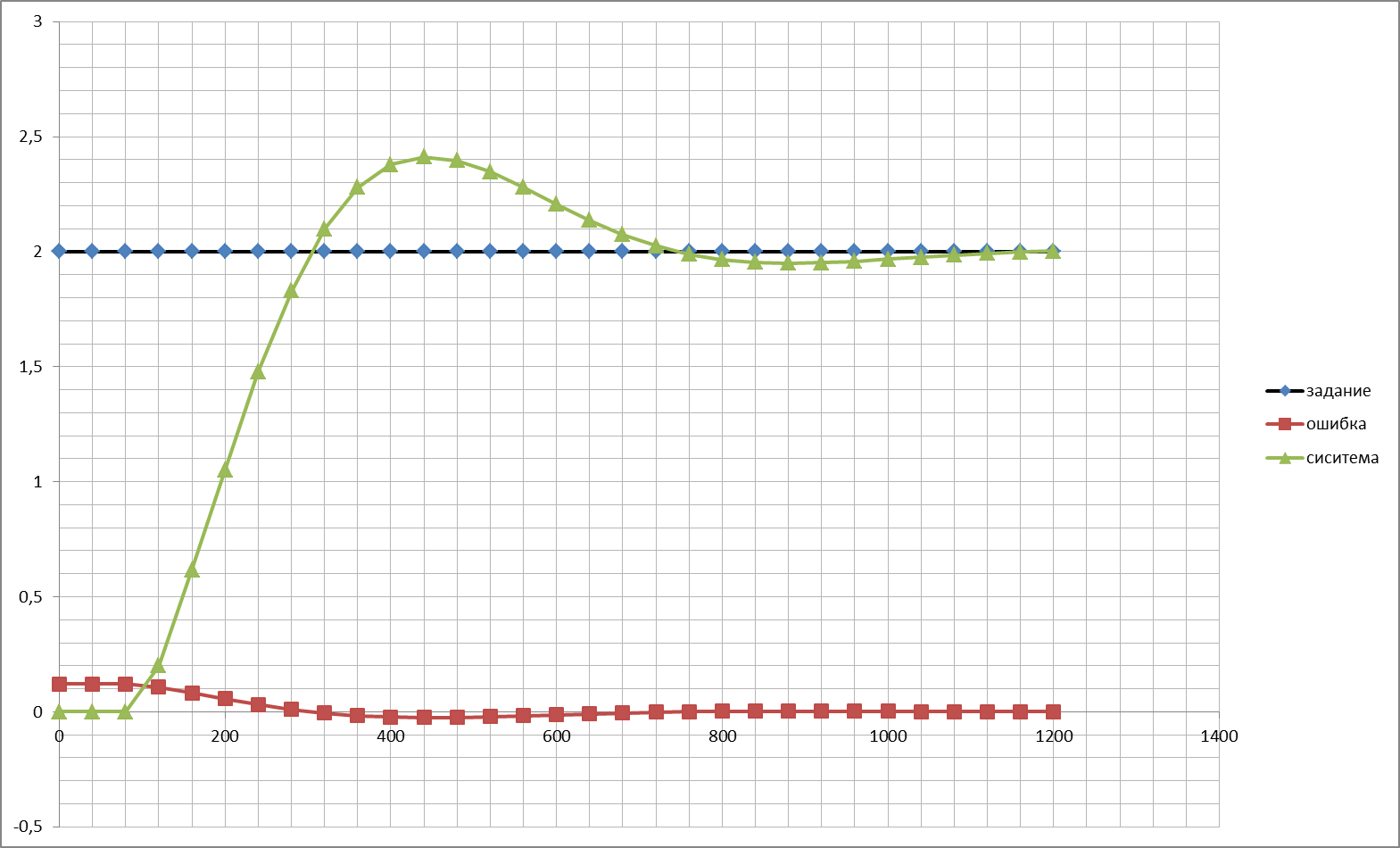
Определение показателей качества системы регулирования по задающему воздействию.

Оценку качества работы системы по задающему воздействию можно получить, анализируя кривую переходного процесса системы.

1. Точность системы управления в установившемся режиме работы.

Этот показатель оценивается величиной установившейся ошибки: ОШ_¥ - точность, с которой поддерживается постоянство регулируемого параметра, определятся как разность между установившимся значением регулируемой величины после окончания переходного процесса y_¥ и её заданным значением g_зад, т.е. ОШ_¥ = y_¥ - g_зад Из графика видно, что

y_¥ = g_зад = 2. это значит, что величина установившейся ошибки ОШ_¥ = 0, т.е. полученная система не имеет систематической ошибки, сигнал на выходе системы, в установившемся режиме, равен сигналу задания.

2. Оценка быстродействия системы.

Быстродействие системы оценивается по времени переходного процесса, от момента начала воздействия до момента времени, после которого верно неравенство: | y(t) - y_¥ | £ D, где D = (0,03-0.05 * y_¥ ).

По графику переходного процесса найдём t_п.пр. = 670с » 11 мин.

Длительность переходного процесса велика.

3. Запас устойчивости (склонность системы к колебательности).

4.

а). перерегулирование – максимальное отклонение регулируемой переменной от установившегося значения.

Величина d -в пределах нормы, (допускается 10 ¸ 30 %).

б). затухание за период.

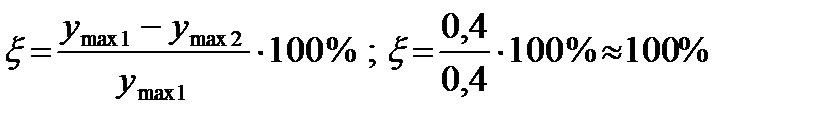
Затухание в допустимых пределах.

в). Число колебаний за время переходного процесса – 1.